Универсальные функции и множества

Лекция № 6. Универсальные функции и множества

1. Универсальные функции и множества

2. Главные универсальные функции и множества

Определение 6.1.1. Функция U двух натуральных аргументов называется универсальной для класса вычислимых функций[6] одного аргумента, если для каждого n функция:

,

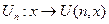является вычислимой функцией, и каждая вычислимая функция одного аргумента встречается среди .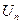

Теорема 6.1.1. Существует вычислимая функция двух аргументов, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.

Доказательство. Пусть p₀, p₁, …p_i,...– последовательность программ[7], вычисляющих функции одного аргумента. Положим U(i, x) равным результату работы i- ой программы на входе x. Тогда U(i, x) – универсальная функция.

¨Теорема доказана.

Определение 6.1.2. Множество 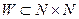называют универсальным для некоторого класса множеств натуральных чисел, если все множества

W_n ={ x: (n, x)Î W }

принадлежат этому классу, и других множеств в этом классе нет.

Теорема 6.1.2. Существует перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел.

Доказательство. Область определения универсальной функции – универсальное перечислимое множество, так как каждое перечислимое множество есть область определения некоторой вычислимой функции.

¨Теорема доказана.

Теорема 6.1.3. Не существует вычислимой всюду определенной функции двух аргументов, универсальной для класса всех вычислимых всюду определенных функций одного аргумента.

Доказательство. Пусть U – произвольная вычислимая всюду определенная функция двух аргументов. Положим u(n)=U(n, n), d(n)=u(n)+1. Всюду определенная функция d(n) отличается от всех 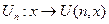, а потому U – не является универсальной.

¨Теорема доказана.

Теорема 6.1.4. Существует вычислимая функция d(n), от которой никакая функция не может отличаться всюду (для любой вычислимой функции найдется nÎN такое, что f(n)=d(n) (равенство понимается в том смысле, либо оба значения f(n) и d(n) не определены, либо оба определены и равны)).

Доказательство. d(n)=U(n, n), где U(n, х) универсальная функция двух аргументов для класса вычислимых функций одного аргумента.

¨Теорема доказана.

Теорема 6.1.5. Существует вычислимая функция, не имеющая всюду определенного вычислимого продолжения.

Доказательство. Пусть d(n)=U(n, n), где U(n, х) универсальная функция двух аргументов для класса вычислимых функций одного аргумента. Положим g(n)=d(n)+1. Тогда при тех значениях n, где функция d(n) определена g(n)¹ d(n) и любое ее продолжение отличается от d. В этом случае предположение о вычислимости всюду определенного продолжения g(n) придет в противоречие с предыдущей теоремой, гласящей об отсутствии вычислимой функции, всюду отличающейся от d(n).

¨Теорема доказана.

Теорема 6.1.6. Существует перечислимое неразрешимое множество.

Доказательство. Область определения F вычислимой функции f(x), не имеющей всюду определенного вычислимого продолжения – перечислимое неразрешимое множество. С одной стороны F – перечислимо. С другой стороны, если бы множество F было бы разрешимо, то функция

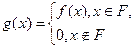
была бы всюду определенным продолжением f(x).

¨Теорема доказана.

Дата добавления: 2014-01-06