Функция распределения и ее свойства. Функция распределения дискретной случайной величины

{X < х} (а не {X = х}), где х — некоторое дей­ствительное число.

Следовательно, вероятность Р{Х < х} является функцией от х.

F_x (х)

Функцией распределения с. в. X называется функция F(x), которая для любого числа х Î R равна вероятности события {X < х}.

F(x)=P{X < х} т.е. F(x)=P{w: X (w)< х} (34)

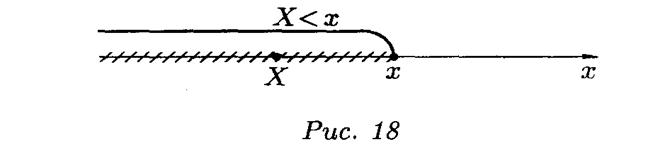
Функция распределения обладает следующими свойствами:

1. 0£F(x)£ 1.

2. F(x) — неубывающая функция на R, т. е. если х₂ > х₁, то

F(x₂)≥F(x₁),

3.F(x) обращается в ноль на минус бесконечности и равна единице в плюс бесконечности, т. е.

F(-¥)=0, F(+¥) = 1.

4.Вероятность попадания с. в. X в промежуток [а, b) равна прираще­нию ее функции распределения на этом промежутке, т. е.

Р{а£Х <b} = F(b)-F(a). (35)

5.F(x) непрерывна слева, т. е.

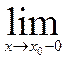F(x) = F(x₀).

1. Первое свойство следует из определения (2.1) и свойств вероят­ности (п. 1.11. 1.12).

2. Пусть А = {X < x₁}, В = {X < x₂}. Если x₁ < х₂, то собы­тие А влечет событие В (п. 1.4), т. е. А Í В. Но тогда согласно свой­ству 4 (п. 1.12), имеем Р(А) £ Р(В), т.е. Р{Х < x₁} £ Р{Х < х₂} или F(x₁) < F(x₂).

Геометрически свойство 2 очевидно: при перемещении точки х вправо по числовой оси вероятность попадания случайной точки X в интервал (—∞,х) не может уменьшаться.

3. Третье свойство вытекает непосредственно из того, что {X < —∞} = Æ, а {X < +∞} = Ώ; согласно свойствам вероятности (п. 1.11, 1.12), имеем: F(-∞) = Р{Х < -∞} = Р{Æ} = 0, F{+∞) = = Р{Х <+∞} = Р{Ώ} = 1.

4. Так как а < b, то очевидно, что {X < b} = {X < а} + {а £ X < b} (это хорошо видно на рис. 19).

Так как слагаемые в правой части — несовместные события, то по теореме сложения вероятностей (п. 1.11) получаем Р{Х < b} = Р{Х < а} + Р{а £ X < b}. Отсюда следует Р{а £ X <b} = = Р{Х <b}- Р{Х < а} = F(b) - F(a).

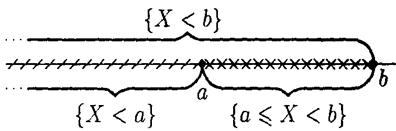
Рис. i9

Всякая функция F(x), обладающая свойствами 1-3, 5, может быть функцией распределения некоторой случайной величины.

Заметим, что формула (2.2) (свойство 4) справедлива и для н. с. в., и для д. с. в.

С помощью функции распределения можно вычислить вероятность события {X ≥ x}:

Р{Х ≥x} = l-F(x). (36)

Используя свойство 4 можно показать, что «вероятность того, что н. с. в. X примет заранее указанное определенное значение a, равна ну­лю».

Действительно, применим формулу (2) к промежутку [a, x): Р{а £X < х}= F(x) — F(a). Будем неограниченно приближать точку х к а. Так как функция F(x) непрерывна в точке а, то 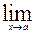F(x) = F(a). В пределе получим Р{Х = а} = 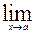F(x) – F(a) = F(a) – F(a) = 0. Если функция F(x) везде непрерывна, то вероятность каждого отдельного значения с. в. равна нулю.

Следовательно, для н.с. в. справедливы равенства

Р{а £х<b} = Р{а < х < b} = Р{а £ х £ b} = Р{Х Î(а. b]}.

Действительно,

Р{а £х<b} =P{X=a} + Р{а < х < b} = Р{а < х < b} }.

и т.д.

Функция распределения д. с. в. имеет вид

F(x) = 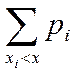(37)

Здесь суммирование ведется по всем i, для которых х_i < x.

Пример 3. По условию примера 2 (п. 20) найти функцию распре­деления F(x) и построить ее график.

X
Р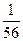

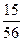
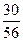
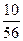
Будем задавать различные значения х и находить для них

F(x)= Р{Х < х}:

1. Если х £ 0, то, очевидно, F(x) = Р{Х < 0} = 0;

2. Если 0 < х £ 1, то F(x) = Р{Х < х} = Р{Х = 0} = ;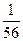

3. Если 1 < х £ 2. то F(x)=Р{Х=0}+Р{Х= 1} = +=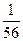

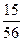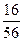
4. Если 2 < x £ 3. то F(x) = Р{Х = 0} + Р{Х = 1} + Р{Х = 2} = ++=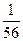

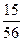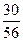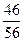
5. Если 3 < х, то F(x) = Р{Х = 0} + Р{Х = 1} + Р{Х = 2} + Р{Х=3}= 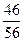+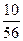=1.

Итак,

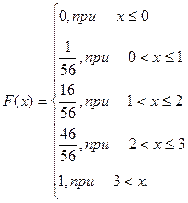
Строим график F(x), рис. 20.

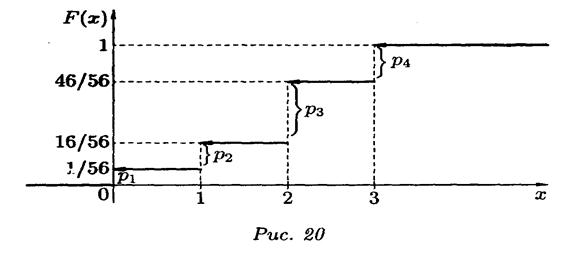
Рис. 20

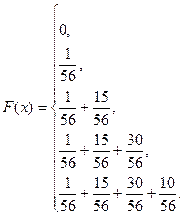
Дата добавления: 2014-01-06