КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проектирование сетей ЭВМ
|
|
|
|
Теория проектирования сетей ЭВМ базируется на аппарате систем массового обслуживания(СМО).
Обозначим n-e требование, поступающее в СМО через 
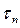 - момент поступления требования
- момент поступления требования 
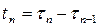 - время между соседними требованиями
- время между соседними требованиями 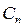 и
и  .
.
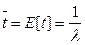 - среднее время между соседними требованиями
- среднее время между соседними требованиями
 - среднее время обслуживания.
- среднее время обслуживания.
Для обозначения различных типов СМО используется обозначение, которое имеет вид A/B/m. Так обозначается СМО с m обслуживающими приборами, а A и B указывают соответственно на распределение времени между соседними требованиями и распределение времени обслуживания. А и В принимают значение из следующего набора символов:
M – показательное распределение (Markovian),  - распределение Эрланга порядка r.
- распределение Эрланга порядка r.
 - гиперпоказательное распределение порядка r, D- постоянная величина(Deterministic),
- гиперпоказательное распределение порядка r, D- постоянная величина(Deterministic),
G – произвольное распределение (General).
Наиболее важным параметром СМО G/G/1 является коэффициент использования 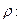
 ,
,
где  - плотность входного потока (средняя скорость поступления требований в систему),
- плотность входного потока (средняя скорость поступления требований в систему),
 - плотность потока обслуживания.
- плотность потока обслуживания.
Эта величина равна доле времени, в течении которого занят единственный обслуживающий прибор, и она также равна отношению требуемой от данной системы скорости обслуживания к пропускной способности системы 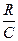 (
( ).
).
Для многолинейной СМО G/G/m
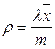
Интерпретируется как математическое ожидание доли занятых приборов, если любой прибор имеет одно и то же распределение времени обслуживания.
В общем случае  - математическое ожидание доли используемой пропускной способности системы. В любой стабильной системе
- математическое ожидание доли используемой пропускной способности системы. В любой стабильной системе 
Случай  не допускается. Чем ближе
не допускается. Чем ближе  к 1, тем больше очереди и время ожидания.
к 1, тем больше очереди и время ожидания.
Среднее время пребывания требования в системе:
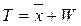
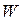 - среднее время ожидания в очереди.
- среднее время ожидания в очереди.
|
|
|
Среднее число требований в очереди:
 - формула Литтла.
- формула Литтла.
Соответствующий результат для числа требований в очереди:
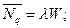
 - средняя длина очереди.
- средняя длина очереди.
Для системы G/G/m справедливо:
 (следует из формулы Литтла).
(следует из формулы Литтла).
 (1)
(1)
Для системы M/M/1 вероятность того, что в системе находится k требований равна
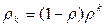 ;
;
Отсюда среднее число требований в системе:
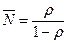 ,
,
а дисперсия равна:
 .
.
Используя формулу Литтла и (1) при m=1 получим две основные характеристики М/M/1 – ее средние характеристики:

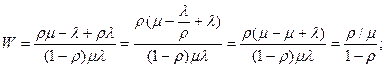
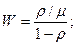
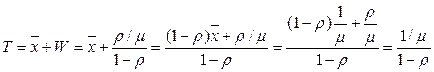 ;
;
 (2)
(2)
Величины  ,
,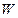 ,
, растут по мере убывания (1-
растут по мере убывания (1- ). При
). При  средние задержки и длины очередей растут неограниченно.
средние задержки и длины очередей растут неограниченно.
Пусть сеть с коммутацией сообщений имеет М каналов и N узлов. Каналы – бесшумные и абсолютно надежные. Пропускная способность i-го канала равна 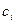 (бит в секунду). Поток, поступающий в сеть из внешних источников(например, из машины HOST)образует Пуассоновский процесс со средним значением
(бит в секунду). Поток, поступающий в сеть из внешних источников(например, из машины HOST)образует Пуассоновский процесс со средним значением 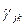 (сообщений в секунду) для тех сообщений, которые возникают в узле j и предназначены для узла k.
(сообщений в секунду) для тех сообщений, которые возникают в узле j и предназначены для узла k.
Полный внешний поток, поступающий в сеть, равен:
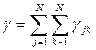 .
.
Длины всех сообщений по предположению независимы и распределены по экспоненциальному закону со средним значением 1/ (бит) (пока не учитывается возможная пакетная структура сообщений).
(бит) (пока не учитывается возможная пакетная структура сообщений).
Для высокоскоростных сетей, покрывающих большие географические расстояния, может оказаться важным включить в рассмотрение время распространения 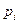 бита через i-ый канал (
бита через i-ый канал ( *скорость света), таким образом если сообщение имеет длину в битах, то время, в течение которого оно занимает канал, равно
*скорость света), таким образом если сообщение имеет длину в битах, то время, в течение которого оно занимает канал, равно  секунд.
секунд.
Заметим, что случайность временного обслуживания появляется не из-за обслуживающего прибора(канала), а из-за требования (сообщения), так как длина сообщения 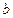 является случайной величиной.
является случайной величиной.
Поскольку любой канал в сети рассматривается как отдельный обслуживающий прибор, обозначим через 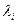 среднее число сообщений в секунду, проходящих через i-ый канал.
среднее число сообщений в секунду, проходящих через i-ый канал.
|
|
|
Как и для внешнего потока, определим полный поток в сети:
 .
.
Предположим, что стоимость построения i-го канала с пропускной способностью  задается некоторой произвольной функцией
задается некоторой произвольной функцией  .
.
Пусть  - стоимость всей сети (по предположению состоит лишь из стоимости каналов):
- стоимость всей сети (по предположению состоит лишь из стоимости каналов):
 .
.
Выше была определена задержка сообщения как такое время, которое сообщение проводит в сети.
Средняя задержка сообщения в сети 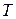 - главная характеристика сети.
- главная характеристика сети.
 [задержка сообщения]
[задержка сообщения]
Обозначим
 [задержка сообщения, которое возникло в j и имеет место назначения k].
[задержка сообщения, которое возникло в j и имеет место назначения k].
Ясно, что
 (3)
(3)
так как доля  полного входящего потока имеет в среднем задержку, равную
полного входящего потока имеет в среднем задержку, равную 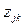 .
.
Последнее равенство представляет разложение сети по параметрам источник – адресат.
При построении сетей возникает множество задач, и к основным из них относятся следующие задачи:
1. выбор пропускной способности каналов { };
};
2. выбор потоков в каналах {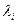 };
};
3. выбор топологии.
Считается, что на стоимость сети накладываются ограничения.
Определим 4 задачи, которые отличаются только множеством переменных, варьируемых при проектировании. В каждой из этих задач считается, что заданы положения узлов, внешний поток 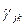 , стоимость каналов
, стоимость каналов  , постоянные D и
, постоянные D и  , а так же предполагается, что используемые потоки {
, а так же предполагается, что используемые потоки {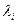 } являются реализуемыми (то есть они согласуются с пропускной способностью и ограничениями на внешний поток, а также удовлетворяют закону сохранения).Первая задача – это выбор пропускных способностей (ВПС).
} являются реализуемыми (то есть они согласуются с пропускной способностью и ограничениями на внешний поток, а также удовлетворяют закону сохранения).Первая задача – это выбор пропускных способностей (ВПС).
Задача ВПС.
| Дано: | потоки {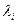 } и топология сети. } и топология сети.
|
| Минимизировать: | 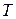 . .
|
| Варьируются: | { }. }.
|
| Ограничение: |  . .
|
Вторая задача – распределение потоков(РП).
Задача РП
| Дано: | Пропускные способности { } и топология сети. } и топология сети.
|
| Минимизировать: | 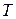 . .
|
| Варьируются: | {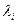 }. }.
|
Третья задача – задача выбора пропускных способностей и распределения потоков(ВПС и РП).
Задача ВПС и РП.
| Дано: | топология сети. |
| Минимизировать: | 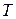 . .
|
| Варьируются: | { }и { }и {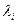 }. }.
|
| Ограничение: |  . .
|
Четвертая задача – задача выбора топологии, пропускных способностей и распределения потоков (ВТ, ПС и РП)
Задача ВТ, ПС и РП.
| Минимизировать: | 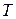 . .
|
| Варьируются: | топология, { }и { }и {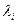 }. }.
|
| Ограничение: |  . .
|
Эти 4 задачи в настоящее время решены с различной степенью полноты.
|
|
|
Обозначим через  путь, по которому идут сообщения, возникшие в узле j, к узлу назначения k. i-ый канал (с пропускной способностью
путь, по которому идут сообщения, возникшие в узле j, к узлу назначения k. i-ый канал (с пропускной способностью  ) включен в путь
) включен в путь  , если сообщения, идущие по этому пути, проходят указанный канал (
, если сообщения, идущие по этому пути, проходят указанный канал ( ). Тогда средняя интенсивность потока сообщений
). Тогда средняя интенсивность потока сообщений 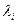 в i-м канале равна сумме средних интенсивностей потоков по всем путям, которые проходят через этот канал, то есть
в i-м канале равна сумме средних интенсивностей потоков по всем путям, которые проходят через этот канал, то есть
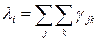 (4)
(4)
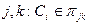
Заметим, что 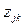 представляет собой сумму средних задержек, испытываемых сообщениями при передаче по различным каналам пути
представляет собой сумму средних задержек, испытываемых сообщениями при передаче по различным каналам пути  .
.
 [время, затраченное на ожидание и процесс передачи по i-му каналу],
[время, затраченное на ожидание и процесс передачи по i-му каналу],
то есть  - среднее время, проведенное сообщением в системе, где под системой понимается i-ый канал:
- среднее время, проведенное сообщением в системе, где под системой понимается i-ый канал:
 (5)
(5)

Отсюда из (3) получаем:
 (6)
(6)

Изменим порядок суммирования, тогда как обычно при изменении порядка суммирования условие на i становится условием на j,k. В результате имеем:

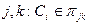
Используя соотношение (4), получаем:
 (7)
(7)
Теперь средняя задержка сообщения разложена на компоненты, относящиеся к отдельным каналам, то есть разложена по  .
.
Предположение о независимости. Всякий раз, когда сообщение принимается в узле внутри сети, независимо с плотностью распределения
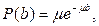
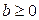
выбирается его новая длина  .
.
Это предположение показано с помощью многочисленных моделирований для реальных сетей. Это утверждение, вообще-то говоря, неверно, так как сообщения сохраняют длину при их прохождении по сети, но как показано, влияние этого предположения на 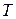 пренебрежимо мало в большинстве сетей.
пренебрежимо мало в большинстве сетей.
Пользуясь этим предположением, получим, что i-ый канал теперь можно рассматривать как систему М/М/1 с пуассоновским потоком интенсивности 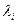 на входе и показательным временем обслуживания со средним 1/
на входе и показательным временем обслуживания со средним 1/ секунд. Решение сразу же получаем из (2).
секунд. Решение сразу же получаем из (2).
 .
.
И поэтому, согласно (5), имеем[1]:
 (8)
(8)
 Анализ (4) показывает, что при увеличении нагрузки на сеть никакое слагаемое в выражении (4) не будет доминировать, пока поток в одном из каналов (например, в
Анализ (4) показывает, что при увеличении нагрузки на сеть никакое слагаемое в выражении (4) не будет доминировать, пока поток в одном из каналов (например, в 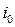 ) не достигнет пропускной способности этого канала по соответствующему узкому месту сети.
) не достигнет пропускной способности этого канала по соответствующему узкому месту сети.
|
|
|
В этой точке  , и следовательно
, и следовательно 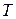 быстро растут, то есть имеется порог по
быстро растут, то есть имеется порог по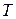 .
.
Это пороговое поведение задержки показано(упрощено) на рис. 9.
|
|

 определяется как задержка в отсутствии нагрузки (незагруженная сеть).
определяется как задержка в отсутствии нагрузки (незагруженная сеть).
Из (4) при 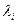 и
и 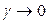 получим:
получим:
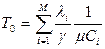 .
.
 - нагрузка насыщения, при которой
- нагрузка насыщения, при которой  .
.
Определим 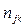 как длину пути
как длину пути  , где над длиной понимается число каналов в пути. Средняя длина пути
, где над длиной понимается число каналов в пути. Средняя длина пути  выражается как
выражается как
 .
.
Рассмотрим полный поток в сети  . Отметим, что вклад потока j-k в полный поток равен
. Отметим, что вклад потока j-k в полный поток равен 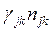 , так как
, так как 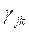 сообщений пройдут
сообщений пройдут 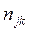 участков при движении по сети.
участков при движении по сети.
Следовательно:
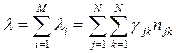 .
.
Из последних двух равенств получаем известный общий результат:
 .
.
Отсюда  .
.
Это дает метод вычисления задержки в отсутствии нагрузки  для упрощенной пороговой модели.
для упрощенной пороговой модели.
Отыскание нагрузки насыщения  выполняется непосредственно. Она соответствует наименьшему значению
выполняется непосредственно. Она соответствует наименьшему значению  , при котором
, при котором  . Поэтому при заданной фиксированной процедуре выбора маршрутов можно просто найти многие {
. Поэтому при заданной фиксированной процедуре выбора маршрутов можно просто найти многие {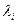 } с помощью формулы
} с помощью формулы
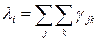
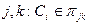
при любом  . После этого нужно посмотреть все отношения и определить
. После этого нужно посмотреть все отношения и определить  на наибольшем из этих отношений. Далее все потоки уменьшаем на масштабируемый коэффициент, при котором
на наибольшем из этих отношений. Далее все потоки уменьшаем на масштабируемый коэффициент, при котором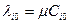 . Значение
. Значение  при котором это равенство будет иметь место равно
при котором это равенство будет иметь место равно  .
.
Весьма важно отыскание максимального потока, который сеть может переносить между данной парой углов. Это можно выполнить с помощью хорошо известной теоремы о максимальном потоке и минимальном сечении. Согласно этой теореме, максимальный поток, который сеть может переносить между некоторым источником (узлом) s и адресатом (узлом) t, равен величине минимального сечения s-t.
Любая совокупность ребер, при устранении которой из сети прерывается весь поток от источника s к адресату t, называется сечением s-t.
Пропускная способность сечения представляет собой полный поток, который устраненные ребра может переносить от источника s к адресату t.
Минимальным сечением s-t называется сечение, которое имеет наименьшую пропускную способность. Существуют алгоритмы нахождения максимального потока между данным источником и адресатом.
Контрольные вопросы:
1. Дайте определение коэффициента использования?
2. Чему равно среднее время пребывания для системы M/M/1? Какая величина называется стоимостью сети?
3. Дайте определение средней задержки в сети. Приведите итоговую формулу.
4. Сформулируйте задачи ВПС, РП, ВПС и РП.
5. Чему равна средняя задержка в канале?
6. Чему равна средняя длина пути в сети?
7. Чему равно среднее время ожидания в очереди для системы M/M/1?
8. Чему равен максимальный поток, который сеть может переносить между некоторым источником и адресатом?
Лекция 4.
Задача выбора пропускных способностей.
Эта задача, усложняется тем, что оптимальный вектор пропускных способностей необходимо делать из конечного набора их возможных значений, то есть задача целочисленного программирования, решается она численными методами аналитического решения в замкнутой форме не имеет. Поэтому будем считать (для теоретического изучения), что пропускная способность выбирается из непрерывного ряда. Считаем, что известна топология и потоки {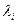 }. Заметим, что
}. Заметим, что  - есть среднее число битов в секунду, которые проходят по i-му каналу, и, следовательно, любое реализуемое решение задачи ВПС должно быть таким, чтобы i-ый канал имел пропускную способность не меньшую указанной величины, то есть чтобы
- есть среднее число битов в секунду, которые проходят по i-му каналу, и, следовательно, любое реализуемое решение задачи ВПС должно быть таким, чтобы i-ый канал имел пропускную способность не меньшую указанной величины, то есть чтобы  . Рассмотрение будем вести для линейных стоимостных функций, то есть
. Рассмотрение будем вести для линейных стоимостных функций, то есть
 ,
,
где  - стоимость в расчете на единицу пропускной способности i-го канала.
- стоимость в расчете на единицу пропускной способности i-го канала.  может меняться от какого-либо параметра канала. Например, он часто берется пропорциональным физической длине канала.
может меняться от какого-либо параметра канала. Например, он часто берется пропорциональным физической длине канала.
Для минимизации 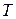 составим функцию Лагранжа.
составим функцию Лагранжа.
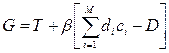 ,где
,где 
Отсюда
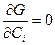 ; что дает
; что дает
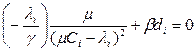 или
или
 .
.
Найдем 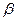 , умножив последнее равенство на
, умножив последнее равенство на 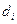 и, просуммировав по i, получим:
и, просуммировав по i, получим:

Откуда
 .
.
Обозначим 
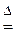
 (9),
(9),
тогда

 (10)
(10)
Это и есть оптимальное решение задачи ВПС. При таком наборе пропускная способность любого канала будет иметь по крайней мере пропускная способность 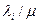 (то есть минимально требуемое значение) и, кроме того, некоторая дополнительная пропускная способность. Отметим, что стоимость минимальной пропускной способности i-го канала равна
(то есть минимально требуемое значение) и, кроме того, некоторая дополнительная пропускная способность. Отметим, что стоимость минимальной пропускной способности i-го канала равна  ; взяв сумму по всем каналам, получим допустимую стоимость. Разность между полной стоимостью и минимально допустимой стоимостью равна
; взяв сумму по всем каналам, получим допустимую стоимость. Разность между полной стоимостью и минимально допустимой стоимостью равна 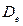 и задается (9). Поэтому
и задается (9). Поэтому 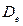 называется добавочной стоимостью.
называется добавочной стоимостью.
Как следует из (9) эта добавочная стоимость сначала нормируется коэффициентом 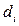 и затем распределяется по всем каналам пропорционально квадратному корню из взвешенной интенсивности потока
и затем распределяется по всем каналам пропорционально квадратному корню из взвешенной интенсивности потока  . Такой оптимальный набор пропускных способностей называется набором пропускных способностей по закону квадратного корня.
. Такой оптимальный набор пропускных способностей называется набором пропускных способностей по закону квадратного корня.
Если подставить (9) в выражение для  , то получим:
, то получим:


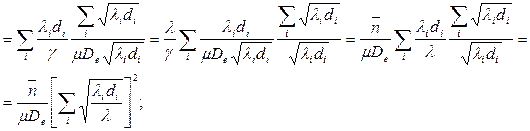
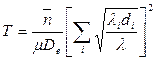 , где
, где  (11)
(11)
Это равенство – минимальная средняя задержка в сети, пропускные способности в которой выбраны оптимально.
При 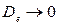 ,
,  . Если
. Если  задача ВПС имеет реализуемое (осуществимое) решение(то есть
задача ВПС имеет реализуемое (осуществимое) решение(то есть 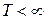 ). Если
). Если  задача не имеет реализуемого решения. Уравнения (10) и (11) дают полное решение ВПС.
задача не имеет реализуемого решения. Уравнения (10) и (11) дают полное решение ВПС.
Рассмотрим частный случай  , при этом, не теряя общности, можно положить d=1. Этот случай имеет место при рассмотрении спутниковых каналов связи, в которых расстояние между двумя различными точками(на Земле, та как логический канал – это узел-узел) в зоне спутника по существу является одинаковым независимо от расстояния между этими точками на поверхности земли. Здесь Если
, при этом, не теряя общности, можно положить d=1. Этот случай имеет место при рассмотрении спутниковых каналов связи, в которых расстояние между двумя различными точками(на Земле, та как логический канал – это узел-узел) в зоне спутника по существу является одинаковым независимо от расстояния между этими точками на поверхности земли. Здесь Если  , то есть сумма всех пропускных способностей сети, которые обозначим как
, то есть сумма всех пропускных способностей сети, которые обозначим как 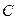 . Тогда выражения для
. Тогда выражения для  и
и 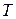
имеют вид:

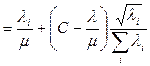
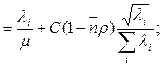
где  (это не коэффициент использования, просто совпадают обозначения),
(это не коэффициент использования, просто совпадают обозначения),  - средняя длина пути;
- средняя длина пути; 
т.е.
 (12)
(12) 
 (13)
(13)
 введена потому, что она является заданной величиной.
введена потому, что она является заданной величиной.
Величина  просто равна отношению
просто равна отношению  (средней скорости, с которой биты входят в сеть от внешних источников) к C(суммарной пропускной способности сети).
(средней скорости, с которой биты входят в сеть от внешних источников) к C(суммарной пропускной способности сети).
Отметим, что  является строго возрастающей функцией от
является строго возрастающей функцией от 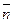 .Это наводит на мысль, что топологию структуры сети, видимо, следует выбирать так, чтобы получить минимальную среднюю длину. Последнее достигается в полносвязной сети(любая пара узлов связана каналом). Кроме того, если рассмотреть сумму в числителе
.Это наводит на мысль, что топологию структуры сети, видимо, следует выбирать так, чтобы получить минимальную среднюю длину. Последнее достигается в полносвязной сети(любая пара узлов связана каналом). Кроме того, если рассмотреть сумму в числителе  , то можно найти, что она минимизируется по множителю {
, то можно найти, что она минимизируется по множителю {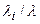 }, когда одна из этих величин равна единице, а остальную сумму в числителе нельзя минимизировать таким образом, так как при этом весь поток будет идти по одному каналу, а остальные будут простаивать. Однако суммирование подсказывает, что нужно посылать большую часть потока по нескольким скоростным каналам и лишь малую часть – по остальным каналам. Обычно для связи требуется по крайней мере один входящий и один выходящий канал для любого узла. Такая сеть представляет собой кольцо, но здесь большая средняя длина пути.
}, когда одна из этих величин равна единице, а остальную сумму в числителе нельзя минимизировать таким образом, так как при этом весь поток будет идти по одному каналу, а остальные будут простаивать. Однако суммирование подсказывает, что нужно посылать большую часть потока по нескольким скоростным каналам и лишь малую часть – по остальным каналам. Обычно для связи требуется по крайней мере один входящий и один выходящий канал для любого узла. Такая сеть представляет собой кольцо, но здесь большая средняя длина пути.
Другая сеть, в которой также имеется один входной и один выходной канал за исключением центрального узла, является звездообразной(см.рис 9).

Рис.10. Звездообразная сеть.
Здесь средняя длина пути 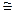 2. Теперь следует сделать выбор между полной сетью, звездообразной сетью и всеми остальными промежуточными меду ними.
2. Теперь следует сделать выбор между полной сетью, звездообразной сетью и всеми остальными промежуточными меду ними.
Показано, что выбор зависит от  . При
. При  наиболее подходящей является звезда, а при
наиболее подходящей является звезда, а при  - полносвязная сеть. Можно ожидать, что между этими двумя экстремальными топологиями приемлемую топологию даст добавление некоторых прямых каналов к звездообразной сети.
- полносвязная сеть. Можно ожидать, что между этими двумя экстремальными топологиями приемлемую топологию даст добавление некоторых прямых каналов к звездообразной сети.
Полученные выше выводы относились к фиксированному процессу выбора маршрута. Даст ли улучшение использование процесса выбора маршрута, допускающего альтернативы?
Такая процедура предлагает более чем 1 путь и, кроме того, она дает упорядочение по предпочтению этих путей – обычно длинные пути менее предпочтительны, чем прямые.
Поэтому допускающие альтернативу процедуры выбора маршрута приводят к увеличению длины пути, и, в то же время, они пытаются распределить поток по многим каналам, а не концентрировать его лишь на нескольких каналах. При допускающей альтернативы процедуре нарушаются оба интуитивных правила, выведенные выше. Результаты моделирования показывают, что следует отказать предпочтение последовательности указанных выше топологий и что фиксированные процедуры выбора маршрута оказываются лучше процедур, допускающих альтернативы. Эти результаты получены в предположении, что величины 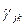 известны и постоянны. Если же они либо неизвестны, либо меняются, либо и то, и другое, то из
известны и постоянны. Если же они либо неизвестны, либо меняются, либо и то, и другое, то из  , где
, где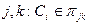 , нельзя найти параметры потока в каналах
, нельзя найти параметры потока в каналах  и, следовательно, оптимальное распределение потока с помощью равенств типа (7). Таким образом, в некоторые периоды времени сеть не будет оптимизированной. Если рассогласование велико, то необходимо введение адаптивной, допускающей альтернативы процедуры для недогруженных путей во время этих интервалов.
и, следовательно, оптимальное распределение потока с помощью равенств типа (7). Таким образом, в некоторые периоды времени сеть не будет оптимизированной. Если рассогласование велико, то необходимо введение адаптивной, допускающей альтернативы процедуры для недогруженных путей во время этих интервалов.
Было заключено, что при линейной стоимостной функции, при минимизации  возможна широкая (и, может быть, нежелательная) вариация значений
возможна широкая (и, может быть, нежелательная) вариация значений 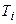 .В результате была поставлена новая задача ВПС, в которой следует минимизировать функцию:
.В результате была поставлена новая задача ВПС, в которой следует минимизировать функцию:



Выбор этой функции обусловлен тем, что большие значения 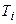 , возведенные в большие степени, увеличивают ее намного больше, чем ранее, так что любая процедура минимизации с k>1 приведет к уменьшению разницы между
, возведенные в большие степени, увеличивают ее намного больше, чем ранее, так что любая процедура минимизации с k>1 приведет к уменьшению разницы между 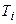 .
.
Решая эту задачу как прежде, получим
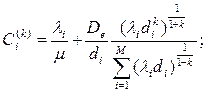
.
При 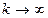 имеем:
имеем:


Отметим, что все 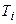 получаются равными.
получаются равными.
При  получим:
получим:


В этом случае пропускная способность прямо пропорциональна (при  ) интенсивности потоков
) интенсивности потоков  ; такой набор пропускных способностей называется пропорциональным набором пропускных способностей, и, по-видимому, очень естественно, что это следует рассматривать прежде всего(на самом деле пропорциональный набор пропускных способностей не далек от оптимального).
; такой набор пропускных способностей называется пропорциональным набором пропускных способностей, и, по-видимому, очень естественно, что это следует рассматривать прежде всего(на самом деле пропорциональный набор пропускных способностей не далек от оптимального).
Более интересно то, что величина  имеет одно и то же значение в этих двух экстремумах(
имеет одно и то же значение в этих двух экстремумах( ), хотя наборы пропускных способностей очень отличаются.
), хотя наборы пропускных способностей очень отличаются.
Контрольные вопросы:
1.Какое оптимальное значение пропускной способности канала в задаче ВПС?
2. Какое оптимальное значение средней задержки в сети?
3.Охарактеризуйте фиксированную процедуру выбора маршрута.
4.Охарактеризуйте процедуру выбора маршрута, допускающую альтернативы.
5. Какая величина называется пропорциональным набором пропускным способностей?
6. Что такое полносвязная сеть?
7. Чему равна средняя длина пути в сети?
8. При каких значениях ρ оптимальной топологией является полносвязная сеть?
Лекция №5
Задача распределения потоков.
В задаче ВПС требовалось оптимально выбрать пропускную способность каналов при заданной конфигурации потоков {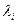 }. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если
}. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если 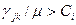 (где
(где  - пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.
- пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.
В качестве исходного выражения для характеристики  используется
используется
 - средняя задержка сообщения в сети.
- средняя задержка сообщения в сети.
То есть требуется минимизировать нелинейную функцию  по потокам {
по потокам {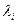 }, чтобы удовлетворились внешние требования к потокам
}, чтобы удовлетворились внешние требования к потокам  и ограничения на пропускную способность любого канала, состоящие в том, что поток
и ограничения на пропускную способность любого канала, состоящие в том, что поток  в канале должен быть неотрицательным и меньшим пропускной способности, то есть
в канале должен быть неотрицательным и меньшим пропускной способности, то есть 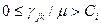 .Это ограничение следует из свойства безграничного возрастания
.Это ограничение следует из свойства безграничного возрастания  при стремлении какого-либо потока к пропускной способности соответствующего канала. На языке математического программирования это означает, что характеристика
при стремлении какого-либо потока к пропускной способности соответствующего канала. На языке математического программирования это означает, что характеристика  включает дополнительное ограничение на пропускную способность как функцию штрафа. Это важное свойство обеспечивает реализуемость при использовании любого метода минимизации, который представляется в виде последовательности «небольших шагов» и на начальном шаге оперирует с реализуемым решением. Таким образом, если начать с реализации решения, то можно пренебречь ограничением на пропускную способность и вследствие этого задача, которая выглядит как задача с ограничением, фактически будет представлять собой задачу без ограничений. Здесь применима любая разумная процедура поиска. Рассмотрим один из таких методов, предложенный Клейнроком.
включает дополнительное ограничение на пропускную способность как функцию штрафа. Это важное свойство обеспечивает реализуемость при использовании любого метода минимизации, который представляется в виде последовательности «небольших шагов» и на начальном шаге оперирует с реализуемым решением. Таким образом, если начать с реализации решения, то можно пренебречь ограничением на пропускную способность и вследствие этого задача, которая выглядит как задача с ограничением, фактически будет представлять собой задачу без ограничений. Здесь применима любая разумная процедура поиска. Рассмотрим один из таких методов, предложенный Клейнроком.
Из выражения для  следует, что
следует, что
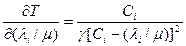 , где
, где 
То есть  и
и  при
при 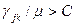 .
.
Отсюда следует, что  - выпуклая функция. Кроме того, множество реализуемых потоков само является выпуклым многогранником. То есть, если задача имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для
- выпуклая функция. Кроме того, множество реализуемых потоков само является выпуклым многогранником. То есть, если задача имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для  .Следовательно можно использовать любой метод отыскания локального минимума при решении задачи поиска глобального минимума.
.Следовательно можно использовать любой метод отыскания локального минимума при решении задачи поиска глобального минимума.
Метод, применяемый здесь, называется методом отклонения потока (ОП). Он предназначен для поиска глобального минимума. Уясним сначала понятие потока по кротчайшим путям. Предположим, что мы имеем сеть, каждый канал которой имеет надписанную на нем длину 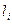 . В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток
. В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток  по этому пути(предполагается, что вопросы, связанные с пропускной способностью и задержкой не рассматриваются). Если поступить так для всех (j,k), то в результате получится поток, который называется потоком, идущим по кратчайшим путям. Существует ряд алгоритмов отыскания таких потоков. Один из них следующий.
по этому пути(предполагается, что вопросы, связанные с пропускной способностью и задержкой не рассматриваются). Если поступить так для всех (j,k), то в результате получится поток, который называется потоком, идущим по кратчайшим путям. Существует ряд алгоритмов отыскания таких потоков. Один из них следующий.
Рассмотрим сеть с  узлами. Пусть
узлами. Пусть  матрица
матрица  , элемент
, элемент 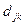 которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того,
которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того,  =0). Для пути
=0). Для пути 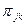 обозначим его длину
обозначим его длину  (сумма длин каналов). Задача состоит в вычислении матрицы
(сумма длин каналов). Задача состоит в вычислении матрицы  порядка
порядка  , где
, где 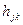 - длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы
- длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы 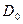 и итеративно изменяет ее, проходя последовательность из
и итеративно изменяет ее, проходя последовательность из  матриц (на n-ом шаге матрица обозначается
матриц (на n-ом шаге матрица обозначается  ); в конце он приходит к матрице кратчайших путей
); в конце он приходит к матрице кратчайших путей 
Если начать с n=0 и 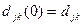 ,то
,то  получается
получается  следующим образом (с помощью итерации)):
следующим образом (с помощью итерации)):
 .
.
Для  заключаем, что
заключаем, что 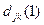 представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания
представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания  получим, что
получим, что 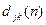 - кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат
- кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат 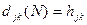 . Весь алгоритм требует
. Весь алгоритм требует 
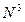 сложений и вычитаний и
сложений и вычитаний и 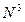 сравнения.
сравнения.
Возвращаясь к исходной задаче сопоставим каждому ребру «длину», которая задается выражением:

Ясно, что это скорость возрастания 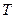 при бесконечно малом увеличении потока
при бесконечно малом увеличении потока  в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения
в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения 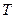 ) пути, к которым может быть отклонена(направлена) некоторая часть потока. Вопрос теперь в том, какая часть исходного потока должна быть отклонена.
) пути, к которым может быть отклонена(направлена) некоторая часть потока. Вопрос теперь в том, какая часть исходного потока должна быть отклонена.
После того как она будет определена, можно повторить процесс опять, находя новые длины, определяя новые кратчайшие маршруты и снова отклоняя поток и так далее до тех пор, пока не будет получена приемлемая характеристика. Введем вектор потока на n-ой итерации:

где i-ая компонента 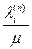 представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток
представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток  является реализуемым.
является реализуемым.
ОПТИМАЛЬНЫЙ АЛГОРИТМ ОП ДЛЯ ВЫБОРА МАРШРУТОВ
1. Положить 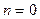 .
.
2. Для каждого 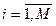 найти
найти

3. Найти 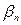 - добавочный стоимостный коэффициент для этого потока:
- добавочный стоимостный коэффициент для этого потока:
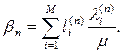
4. Решить задачу отыскания потоков по кратчайшим маршрутам, используя длины  . Пусть
. Пусть  - результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через
- результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через 
5. Найти  - добавочный стоимостный коэффициент для потока по кратчайшему маршруту:
- добавочный стоимостный коэффициент для потока по кратчайшему маршруту:

6. (Правило остановки) Если 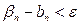 , где
, где 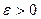 (выбранный допуск), то STOP. В противном случае перейти к п.7.
(выбранный допуск), то STOP. В противном случае перейти к п.7.
7. Найти такое 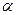 из интервала
из интервала , для которого поток
, для которого поток  минимизирует
минимизирует 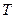 (например, методом Фибоначчи). Оптимальное значение
(например, методом Фибоначчи). Оптимальное значение 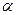 обозначим
обозначим  .
.
8. (Отклонение потока). Положить 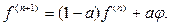
9. Положить 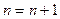 . Перейти к шагу 2.
. Перейти к шагу 2.
Заметим, что отклонение потока производится так, чтобы имело место максимальное снижение значения 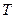 . В общем случае это приводит к детерминированной процедуре выбора маршрутов, допускающей альтернативы.
. В общем случае это приводит к детерминированной процедуре выбора маршрутов, допускающей альтернативы.
Метод ОП обеспечивает оптимальный выбор и является сравнительно эффективным с точки зрения вычислений, однако оказалось, что существует более простой подоптимальный метод, который дает фиксированная процедура выбора маршрута и часто приводит к очень хорошим результатам, требуя намного меньше вычислений. Этот метод обходит задачу определения того, какую часть потока нужно отклонит; ОП просто решает, отклонить весь поток или ничего не отклонять для любого  . Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы
. Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы  в основном не отличаются друг от друга. В сбалансированной сети вклад трафика j-k в любой канал пренебрежимо мал по сравнению с полным потоком в канале. Если это имеет место, то нетрудно понять, почему рассмотрение фиксированной процедуры выбора маршрутов (отклоняется все или ничего) приводит к хорошему приближению. Опять предположим, что известен начальный реализуемый поток
в основном не отличаются друг от друга. В сбалансированной сети вклад трафика j-k в любой канал пренебрежимо мал по сравнению с полным потоком в канале. Если это имеет место, то нетрудно понять, почему рассмотрение фиксированной процедуры выбора маршрутов (отклоняется все или ничего) приводит к хорошему приближению. Опять предположим, что известен начальный реализуемый поток  , направляемый фиксированной процедурой выбора маршрута.
, направляемый фиксированной процедурой выбора маршрута.
АЛГОРИТМ ОТЫСКАНИЯ ПОТОКОВ, НАПРВЛЯЕМЫХ ФИКСИРОВАННОЙ ПРОЦЕДУРОЙ ВЫБОРА МАРШРУТОВ
1. Положить 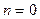 .
.
2. Используя поток  , найти множество кратчайших маршрутов
, найти множество кратчайших маршрутов
(по метрике  ).
).
3. Положить 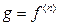 . Для каждого
. Для каждого  сделать следующие шаги:
сделать следующие шаги:
3а. Пусть  - поток, полученный из
- поток, полученный из  путем отклонения всего потока
путем отклонения всего потока  от его пути в потоке
от его пути в потоке  к кратчайшему пути j-k.
к кратчайшему пути j-k.
3б. Если справедливы два утверждения:  - реализуемый поток и
- реализуемый поток и 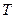 , относящееся к
, относящееся к  , строго меньше, чем
, строго меньше, чем 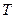 для
для  , то перейти к шагу 3в. В противном случае к шагу 3г.
, то перейти к шагу 3в. В противном случае к шагу 3г.
3в. 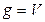 .
.
3г. Если все потоки  рассмотрены – перейти к шагу 4. В остальных случаях выбрать любой нерассмотренный поток
рассмотрены – перейти к шагу 4. В остальных случаях выбрать любой нерассмотренный поток  и перейти к 3а.
и перейти к 3а.
4. Если 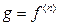 , то STOP: этот метод больше не может улучшить поток. В остальных случаях положить
, то STOP: этот метод больше не может улучшить поток. В остальных случаях положить  ,
, 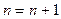 и перейти к шагу 2.
и перейти к шагу 2.
Этот алгоритм сходится после конечного числа шагов, так как нужно рассмотреть конечное число потоков  .
.
Заметим, что по результатам моделирования (на сети ARPA) более быстрый подоптимальный алгоритм дает результаты, отклоняющиеся в пределах 2% от результата оптимального алгоритма.
Задача выбора пропускных способностей и распределения потоков (ВПС и РП).
Ранее были даны оптимальные решения задач ВПС и РП. Объединив эти задачи в задачу ВПС и РП, мы не сможем найти глобально оптимальные решения, но зато опишем процедуры поиска локальных минимумов для 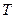 .
.
Так как нужно опять выбирать 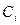 , то представляется, что фиксированные процедуры выбора маршрутов также должны быть оптимальными. Известно, что в случае линейных стоимостных функций (
, то представляется, что фиксированные процедуры выбора маршрутов также должны быть оптимальными. Известно, что в случае линейных стоимостных функций ( ) фиксированные процедуры выбора маршрутов являются оптимальными; это справедливо в силу свойства вогнутости
) фиксированные процедуры выбора маршрутов являются оптимальными; это справедливо в силу свойства вогнутости 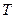 . Кроме того, как можно показать, локальные минимумы
. Кроме того, как можно показать, локальные минимумы 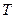 получаются на потоках по кратчайшим маршрутам (подкласс потов, направленных фиксированной процедурой выбора маршрутов), так как минимумы должны располагаться в узлах выпуклого многогранника реализуемого множества потоков.
получаются на потоках по кратчайшим маршрутам (подкласс потов, направленных фиксированной процедурой выбора маршрутов), так как минимумы должны располагаться в узлах выпуклого многогранника реализуемого множества потоков.
Подход к отысканию этих локальных минимумов состоит в том, чтобы начиная с реализуемого начального потока получить оптимальный набор пропускных способностей при линеаризованных стоимостях, с помощью алгоритма ОП найти оптимальные потоки, повторить решение задачи ВПС для этих новых потоков и продолжать итерации к решениям задачи ВПС и задачи РП до отыскания (локального) минимума. Заметим, в частности, что алгоритм ОП будет особенно простым в этом случае, так как значение 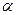 всегда будет равно единице (поток, направленный фиксированной процедурой выбора маршрутов). Таким образом, при известном реализуемом начальном потоке
всегда будет равно единице (поток, направленный фиксированной процедурой выбора маршрутов). Таким образом, при известном реализуемом начальном потоке  алгоритм состоит в следующем:
алгоритм состоит в следующем:
ПОДОПТИМАЛЬНЫЙ АЛГОРИТМ ВПС И РП.
1. Положить 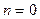 .
.
2. Выполнить алгоритм ВПС для потока  и найти оптимальное множество пропускных способностей, используя линеаризованные стоимости.
и найти оптимальное множество пропускных способностей, используя линеаризованные стоимости.
3. Используя длины  , выполнить алгоритм ОП при
, выполнить алгоритм ОП при  на каждом шаге. Полученный в результате оптимальный поток обозначается через
на каждом шаге. Полученный в результате оптимальный поток обозначается через  .
.
4. Если 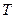 для
для  больше либо равен
больше либо равен 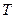 для
для  , то STOP; поток
, то STOP; поток  дает локальный минимум. В противном случае положить
дает локальный минимум. В противном случае положить 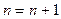 и прейти к шагу 2.
и прейти к шагу 2.
Алгоритм сходится, так как имеется лишь конечное число потов по кратчайшим маршрутам.
При этом  (из формулы
(из формулы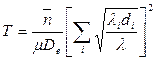 ) задается равенством:
) задается равенством:

 .
.
Отсюда следует, что  и отрицательные циклы существовать не могут
и отрицательные циклы существовать не могут
(что требует алгоритм отыскания кратчайших путей). Заметим, что  это значит, что если в итерации поток (и, следовательно, пропускная способность) обращается в нуль, то как поток, так и пропускная способность, остаются нулевыми при последующих итерациях, так как добавочная стоимость размещения потока становится бесконечной и отклоняемый поток превысит нулевую пропускную способность.
это значит, что если в итерации поток (и, следовательно, пропускная способность) обращается в нуль, то как поток, так и пропускная способность, остаются нулевыми при последующих итерациях, так как добавочная стоимость размещения потока становится бесконечной и отклоняемый поток превысит нулевую пропускную способность.
Теперь перед нами стоят 2 задачи: 1). найти реализуемый начальный поток  и 2). Просматривая многие локальные минимумы отыскать глобальный минимум. Решим обе задачи, повторяя алгоритм ВПС и РП для многих различных начальных реализуемых потоков. Каждый начальный реализуемый поток находится путем случайного назначения каналам исходных длин. Для каждого назначения затем выполняется алгоритм отыскания потоков по кратчайшим путям, использующий выбранные таким образом длины, и проверка условия
и 2). Просматривая многие локальные минимумы отыскать глобальный минимум. Решим обе задачи, повторяя алгоритм ВПС и РП для многих различных начальных реализуемых потоков. Каждый начальный реализуемый поток находится путем случайного назначения каналам исходных длин. Для каждого назначения затем выполняется алгоритм отыскания потоков по кратчайшим путям, использующий выбранные таким образом длины, и проверка условия 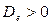 для этого потока. Если условия удовлетворяются, то найдем реализуемый начальный поток и можем приступить к алгоритму ВПС и РП, в противном случае исходный поток отвергается и делается попытка случайного назначения множества других длин. Так как алгоритм ВПС и РП устраняет некоторые каналы при итерациях, приводящих к (локальным) минимумам, то его можно использовать как вспомогательное средство при топологическом проектировании сетей (то есть в задаче ВТПС и РП).
для этого потока. Если условия удовлетворяются, то найдем реализуемый начальный поток и можем приступить к алгоритму ВПС и РП, в противном случае исходный поток отвергается и делается попытка случайного назначения множества других длин. Так как алгоритм ВПС и РП устраняет некоторые каналы при итерациях, приводящих к (локальным) минимумам, то его можно использовать как вспомогательное средство при топологическом проектировании сетей (то есть в задаче ВТПС и РП).
Задачу ВПС и РП можно сформулировать в двойственной форме:
| Дано: | топология сети. |
| Минимизировать: |  . .
|
| Варьируются: | { }и { }и {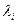 }. }.
|
| Ограничение: | 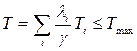 . .
|
Описанный выше алгоритм ВПС и РП применим к этой двойственной задаче, если заменить определение длины  новым определением
новым определением 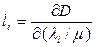 .
.
При линейной ( ) стоимостной функции пропускных способностей выражения для
) стоимостной функции пропускных способностей выражения для 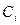 и
и идентичны ранее полученным для
идентичны ранее полученным для 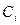 и
и 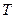 (получаются таким же способом).
(получаются таким же способом).
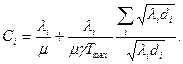


|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!