Постановка задачи. Отметим, что способы обращения к функции fminsearch( )и список ее формальных параметров аналогичны способам обращения к функции Fsolve( ) и списку ее

План

1.7913

0.8896

Отметим, что способы обращения к функции fminsearch() и список ее формальных параметров аналогичны способам обращения к функции Fsolve() и списку ее формальных параметров.

ЛЕКЦИЯ № 5. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

5.1. Постановка задачи

5.2. Интерполяционный полином Лагранжа

5.3. Интерполяционный полином Ньютона для равноотстоящих узлов

5.3.1. Конечные разности

5.3.2. Первый интерполяционный полином Ньютона

5.3.3. Второй интерполяционный полином Ньютона

5.4. Погрешность метода многочленной интерполяции

5.5. Сплайн-интерполяция

5.6. Решение задачи одномерной интерполяции средствами пакете MATLAB

Пусть известные значения некоторой функции f (x) образуют следующую таблицу:

Таблица 5.1

x	x 0	x 1	…	xn
f (x)	y 0	y 1	…	yn

Требуется получить значение функции f(x) для значения аргумента xÎ[x₀,x_n], несовпадающего ни с одним из значений х_i (i = 0, 1,.., n).

Решение задачи находится отысканием некоторой приближающей функции F (x), близкой в некотором смысле к функции f (x), для которой известно аналитическое выражение/

Классический подход к решению задачи построения приближающей функции основан на требовании строгого совпадения значений функций f (x) и F (x) в точках

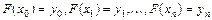. (5.1)

В данном случае нахождение приближенной функции называется интерполированием, а точки 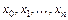называются узлами интерполяции.

Будем искать интерполирующую функцию F (x) в виде многочлена степени n:

. (5.2)

Условия (5.1), наложенные на многочлен, позволяют однозначно определить его коэффициенты. Действительно, требуя для выполнения условий (5.1), получаем линейную систему, состоящую из уравнения:

. (5.3)

Решив систему (5.3) относительно неизвестных 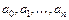, находим значения этих неизвестных и, подставив в (5.2), находим аналитическое выражение аппроксимирующей функции.

Система (5.3) всегда имеет единственное решение, т. к. ее определитель

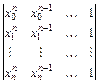, (5.4)

известный в алгебре как определитель Вандермонда, отличен от нуля.

Следовательно, интерполяционный многочлен существует и единственен.

Решение задачи интерполяции в пакете MATLAB с помощью полинома n -ой степени находится выполнением следующей последовательности команд:

1. Задать табличные значения интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Выполнить визуализацию табличной зависимости и истинных значений функции (рис. 5.1)

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X);

>> plot(x,y,'o');

>> hold on

>> plot(X,Y)

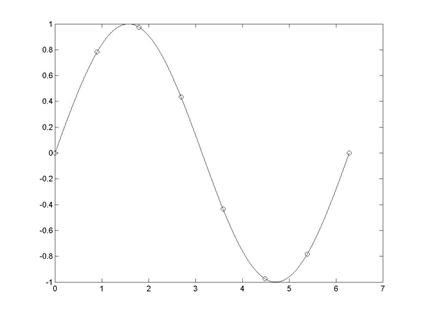
Рис. 5.1

3. Создать файл Pol.m, содержащего описание функции, возвращающей значения полинома (5.2)

% листинг файла Pol.m

function z=Pol(x,a)

N=length(a);

M=length(x);

for j=1:M

s=0;

for i=1:N

s=s+a(i)*x(j).^(N-i);

end;

z(j)=s;

end;

4. Создать файл Vandermod.m, содержащий описание функции, возвращающей значения элементов матрицы Вандермонда

% листинг файла Vandermond.m

function z=Vandermond(x)

N=length(x);

z=ones(N,N);

for i=1:N

for j=1:N

z(i,j)=x(i).^(N-j);

end;

end;

5. Вычислить значения элементов матрицы Вандермонда

>> M=Vandermond(x);

6. Вычислить значения коэффициентов полинома

>> a=M^-1*y';

7. Вычислить значения полинома в заданных промежуточных точках

>> Y1=Pol(X,a);

8. Построить разность между точным и интерполированными значениями функции (рис. 5.2)

Рис. 5.2. Погрешность аппроксимации функции sin (x) полиномом 8-й степени

Дата добавления: 2014-01-06