
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные уравнения электродинамики в комплексной форме
|
|
|
|
При передаче информации посредством ЭМ поля описывающие его векторы меняются во времени. Мгновенные значения векторов поля Е(p,t), D(p,t), Н(p,t), В(p,t), вектора плотности тока j(p,t) и плотности заряда  можно представить в виде интегралов Фурье (прямого преобразования Фурье). Обозначим мгновенное значение любого из векторов ЭМ поля через a(p,t). Тогда применяя к нему преобразование Фурье, получаем:
можно представить в виде интегралов Фурье (прямого преобразования Фурье). Обозначим мгновенное значение любого из векторов ЭМ поля через a(p,t). Тогда применяя к нему преобразование Фурье, получаем:
 (31)
(31)
где 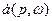 -комплексная амплитуда, или спектральная плотность соответствующего вектора,
-комплексная амплитуда, или спектральная плотность соответствующего вектора, 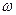 -частота, i- мнимая единица.
-частота, i- мнимая единица.
Подставляя значения преобразований Фурье векторов поля в первое уравнение Максвелла, меняя последовательность выполнения операций ротора и дифференцирования по времени, учитывая, что  , умножим результат на множитель
, умножим результат на множитель  , где
, где 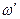 -фиксированная частота. Этот множитель можно внести под знак интеграла. Выполним интегрирование полученного выражения по переменной t в пределах от
-фиксированная частота. Этот множитель можно внести под знак интеграла. Выполним интегрирование полученного выражения по переменной t в пределах от  до
до  . Получаем, меняя порядок интегрирования и сокращая множитель
. Получаем, меняя порядок интегрирования и сокращая множитель  :
:
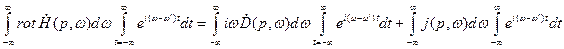
Учитывая здесь, что интеграл по времени есть интеграл Фурье  -функции и сокращая множитель 2
-функции и сокращая множитель 2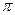 , имеем:
, имеем:

Применяя при интегрировании по со основное свойство  -функции, получаем:
-функции, получаем:
 , откуда, возвращаясь к частоте
, откуда, возвращаясь к частоте 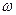 (выполнив замену
(выполнив замену  ), имеем:
), имеем:
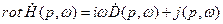 (32)
(32)
Применив аналогичные операции к остальным трем уравнениям Максвелла, получаем
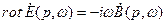 , (33)
, (33)
 ,
, 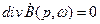
Систему уравнений (32), (33) называют системой уравнений Максвелла в комплексной форме (уравнениями Максвелла для комплексных амплитуд).
Предположим, что в линейной изотропной среде отсутствуют диэлектрический и магнитный гистерезисы. Использовав при этом преобразования Фурье для D(p,t), В(p,t),  , Е'(р,г) и j(p,t), получаем материальные уравнения в комплексной форме (для комплексных амплитуд):
, Е'(р,г) и j(p,t), получаем материальные уравнения в комплексной форме (для комплексных амплитуд):
|
|
|

 (34)
(34)
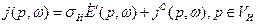 ;
; 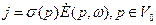 (35)
(35)
где считается, что в случае задания сторонней напряженности поля 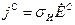 .
.
Применимость материальных уравнений в простой форме ограничена, так как в них не учитывается явление запаздывания во времени электрической поляризации и намагничивания, наблюдаемые в веществах на высоких частотах (частотная дисперсия).
Так как в общем виде  ,
,  ,
, 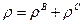 , то находим тем же путем закон сохранения электрического заряда в комплексной форме (для комплексных амплитуд):
, то находим тем же путем закон сохранения электрического заряда в комплексной форме (для комплексных амплитуд):
 ;
;  (36)
(36)
Многие задачи возбуждения ЭМ поля изучаются при одинаковых параметрах сред в области 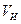 источника и в объеме
источника и в объеме  . Тогда
. Тогда  ,
,  ,
,  и
и  ,
, 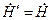 ,
,
 ,
, 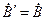 . Сторонние токи
. Сторонние токи  заданы при этом в области
заданы при этом в области 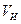 и закон Ома имеет одинаковый вид во всем объеме V
и закон Ома имеет одинаковый вид во всем объеме V
 ,
,  (37)
(37)
Подставляя материальные уравнения 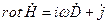 , получаем уравнения Максвелла для комплексных амплитуд векторов напряженностей поля:
, получаем уравнения Максвелла для комплексных амплитуд векторов напряженностей поля:


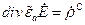
 (38)
(38)
где 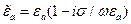 — абсолютная комплексная диэлектрическая проницаемость среды (не является комплексной амплитудой).
— абсолютная комплексная диэлектрическая проницаемость среды (не является комплексной амплитудой).
В первом уравнении Максвелла слагаемое 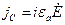 описывает плотность тока смещения
описывает плотность тока смещения  . Второе слагаемое
. Второе слагаемое  — это плотность тока проводимости. Если в веществе плотность тока проводимости намного больше плотности тока смещения, т.е.
— это плотность тока проводимости. Если в веществе плотность тока проводимости намного больше плотности тока смещения, т.е.  , то вещество называют проводником. Если в веществе плотность тока проводимости намного меньше плотности тока смещения, т.е.
, то вещество называют проводником. Если в веществе плотность тока проводимости намного меньше плотности тока смещения, т.е.  , то вещество называют диэлектриком. Таким образом, одно и то же вещество на разных частотах может быть диэлектриком, проводником и полупроводником.
, то вещество называют диэлектриком. Таким образом, одно и то же вещество на разных частотах может быть диэлектриком, проводником и полупроводником.
При математическом моделировании применяются понятия идеального проводника и идеального диэлектрика. Если 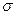 = 0, то ток проводимости отсутствует, вещество— идеальный диэлектрик. Если
= 0, то ток проводимости отсутствует, вещество— идеальный диэлектрик. Если  вещество называют идеальным проводником. Для него
вещество называют идеальным проводником. Для него
 .
.
Если тело считается идеальным диэлектриком, то джоулевы потери в нем отсутствуют поскольку 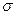 = 0. Если тело считается идеальным проводником, то ЭМ поле в него не проникает, т.е.
= 0. Если тело считается идеальным проводником, то ЭМ поле в него не проникает, т.е.  ,
, 
Магнитное поле не изменяется ни при каких физических процессах в теле. Это значит, что внутри идеального проводника переменное во времени магнитное поле существовать не может. Таким образом, в идеальном проводнике  ,
,  Поэтому, тело идеальной проводимости, находящееся в ЭМ поле, джоулевых потерь в поле не вносит.
Поэтому, тело идеальной проводимости, находящееся в ЭМ поле, джоулевых потерь в поле не вносит.
|
|
|
5. Учтем явление гистерезиса в линейных изотропных средах. Если в выражениях, изученных ранее применить преобразования Фурье для векторов ЭМ поля и для функций  ,
, 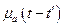 под знаком интеграла, то умножая результат на
под знаком интеграла, то умножая результат на 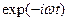 и интегрируя полученное выражение по t от
и интегрируя полученное выражение по t от  до
до  , учитывая значение интеграла Фурье
, учитывая значение интеграла Фурье  -функции, получаем:
-функции, получаем:
 ;
;  ; (39)
; (39)
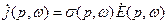
где  и
и  являются комплексными функциями частоты.
являются комплексными функциями частоты.
Учитывая, что 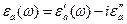 , где
, где 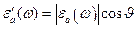 ,
,  , получаем при отсутствии линейного магнитного гистерезиса:
, получаем при отсутствии линейного магнитного гистерезиса:
 (40)
(40)
 ;
; 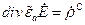 ;
; 
Если ее представить в показательной форме: 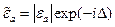 , то
, то 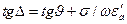 называется тангенсом угла
называется тангенсом угла 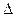 — электрических потерь. Он определяется отношением активной части плотности тока в веществе к его реактивной части.
— электрических потерь. Он определяется отношением активной части плотности тока в веществе к его реактивной части.
При отсутствии линейного электрического гистерезиса 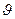 = 0 имеем
= 0 имеем 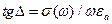 т.е. тангенс угла электрических потерь при этом определяется только отношением плотностей токов проводимости и смещения.
т.е. тангенс угла электрических потерь при этом определяется только отношением плотностей токов проводимости и смещения.
Проводимости проводников и диэлектриков могут отличаться на много порядков. Проводимости металлов (серебра, латуни, меди, железа и др.) превосходят проводимости хороших диэлектриков (полистирола, слюды) на 18-22 порядка в широком диапазоне частот. На рис. 2 приведены (экспериментальные) графики зависимостей проводимостей и относительных диэлектрических проницаемостей  от частоты / для глины (1), песка (2), пресной (3) и морской (4) воды при температуре 20° С (В[ — влажность 4%, В2 — влажность 15%). Как видно из графиков, диэлектрическая проницаемость и удельная проводимость, кроме частоты, зависят от температуры и влажности вещества.
от частоты / для глины (1), песка (2), пресной (3) и морской (4) воды при температуре 20° С (В[ — влажность 4%, В2 — влажность 15%). Как видно из графиков, диэлектрическая проницаемость и удельная проводимость, кроме частоты, зависят от температуры и влажности вещества.
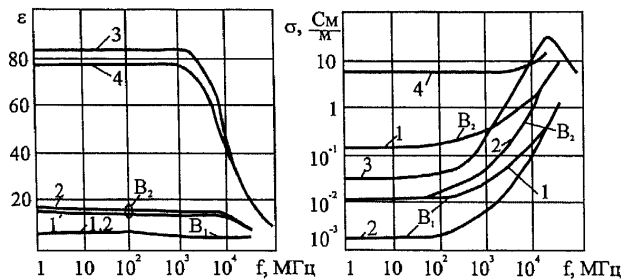
Рис.2 Графики частотной зависимости 1
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1837; Нарушение авторских прав?; Мы поможем в написании вашей работы!