Определение подходящего направления

Для описания алгоритма выбора наилучшего направления поиска очередной точки минимизирующей последовательности введём ряд важных понятий.

Определение 13.3. Ограничение 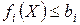(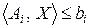) называется

активным в фиксированной точке 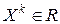, если

().

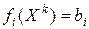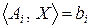Введём в рассмотрение множества индексов активных ограничений

в фиксированной точке 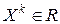: 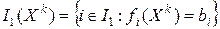- индексное множество активных нелинейных ограничений; - индексное множество активных линейных ограничений;

;.

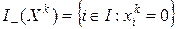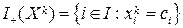
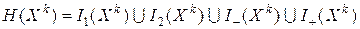Введем в рассмотрение множество n -мерных векторов 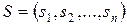в точке 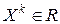и построим множество

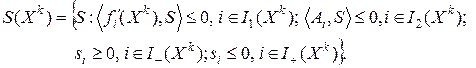
Множество 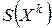представляет собой конус возможных направлений в точке . Если - внутренняя точка множества R, то множество 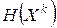пусто, т.е. в этой точке нет активных ограничений, и на выбор вектора S не накладывается никаких ограничений.

Введем искусственную переменную 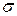и определим множество (n +1)-мерных векторов 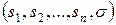следующим образом:

.

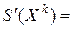
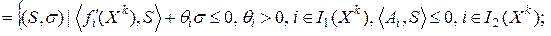
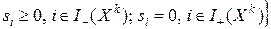Задачу выбора подходящего направления сформулируем как задачу линейного программирования:

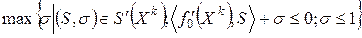. (13.7)

Очевидно, что при 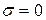множества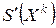и 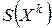совпадают. Если 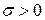, то из ограничения 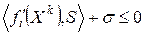следует, что 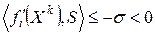и направление 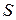будет подходящим. В этом случае 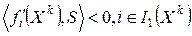, т.е. 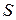не направлено по касательной к нелинейным границам. При этом, чем больше 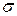, тем больше отличается от нуля 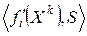, т.е. тем больший угол образуется между 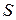и внешней нормалью 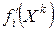. Если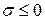, то точка оказывается точкой минимума функции .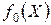

Присутствие в задаче (13.7) ограничения 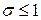объясняется следующим образом. Когда речь идёт о выборе направления, нас интересует именно направление, которое задаётся некоторым вектором произвольной длины. Но при решении ЗЛП (13.7) величина 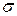может оказаться неограниченной. Чтобы этого избежать следует наложить на длину S некоторые ограничения. Поэтому в постановке задачи (13.7) должно присутствовать так называемое условие нормализации. Таким условием может быть одно из следующих ограничений:

№1..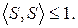

№2.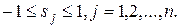

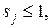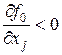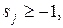№3.если или если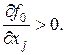

№4.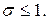

Признак оптимальности в задаче выбора наилучшего подходящего направления устанавливается следующей теоремой.

Теорема 13.2. Точка 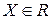является точкой минимум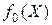а на 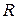, регулярном по Слейтеру тогда и только тогда, когда 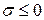для всех 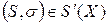, удовлетворяющих неравенству .

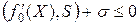Д о к а з а т е л ь с т в о.Если в решении 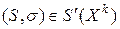задачи выбора направления (13.7) окажется, что 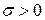, то соответствующее направление 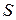будет подходящим, и точка не может быть точкой минимума функции .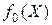

Пусть теперь 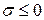для всех 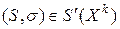, удовлетворяющих условиям

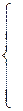
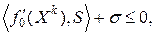
		(13.8)
	(13.9)
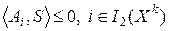
	(13.10)

Будем считать для сокращения записей, что в (13.10) содержатся также и прямые ограничения на переменные задачи .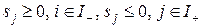

Введя в рассмотрение 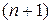- мерные вектора 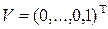, 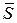неравенство 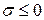можно записать в виде

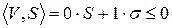
В силу теоремы Фаркаша, устанавливающей равносильность условий

,

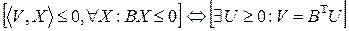найдется такой вектор 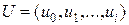, , 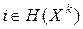что имеют место равенства

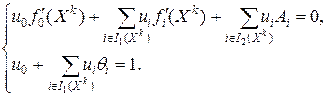
	(13.11)
(13.12)

Если 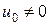, т.е. 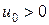, то из (13.11)

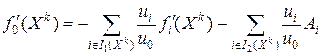, (13.13)

Умножая скалярно равенство (13.13) на некоторый произвольный вектор 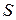, принадлежащий множеству 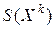получим

.

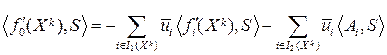Но в множестве 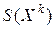выполняются условия 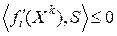и 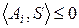для любого 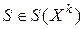. Следовательно, 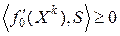для любого 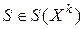, а значит в точке нет подходящего направления и она является точкой минимума функции 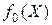на .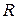

Если 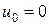, то из условия 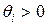и равенства (13.12) следует существование по крайней мере одного 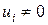, 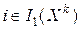. Тогда умножая (13.11) на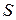

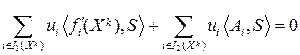(13.14)

Но из регулярности по Слейеру следует существование точки 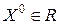такой, что 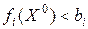для всех 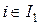. Тогда, полагая 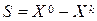, в силу теоремы 12.5 имеем

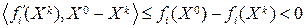
т.к. 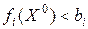, а 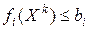. Таким образом, хотя бы одно из слагаемых в (13.14) строго меньше нуля а все остальные неположительны. Поэтому левая часть равенства (13.14) не может быть равна нулю, т.е. случай 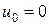невозможен. Теорема доказана.

Контрольные вопросы

1. В чем заключается основная идея метода возможных направлений?

2. Какое направление называется возможным в допустимой точке?

3. Поясните понятие подходящего направления в допустимой точке.

4. Какие ограничения называются активными в фиксированной точке?

5. Какой метод решения задачи выпуклого программирования называется методом возможных направлений?

6. Приведите алгоритм построения начального приближения в методе возможных направлений.

7. Опишите процедуру построения очередной точки минимизирующей последовательности в методе возможных направлений.

8. Дайте определение конуса возможных направлений в точке.

9. Опишите постановку вспомогательной задачи для выбора наилучшего подходящего направления в допустимой точке.

10. Сформулируйте признак оптимальности в задаче выбора наилучшего подходящего направления в допустимой точке.

Дата добавления: 2014-01-06