Формулировка математической задачи оптимизации

Объединяя результаты предыдущих этапов построения математической модели, ее записывают в виде математической задачи оптимизации, включающей построенную целевую функцию и найденные ограничения на управляемые переменные. В достаточно общем виде математическую задачу оптимизации можно сформулировать следующим образом: минимизировать (максимизировать) целевую функцию с учетом ограничений на управляемые переменные.

Под минимизацией (максимизацией) функции переменных на заданном множестве - мерного векторного пространства понимается определение хотя бы одной из точек минимума (максимума) этой функции на множестве , а также, если это необходимо, и минимального (максимального) на значения .

При записи математических задач оптимизации в общем виде обычно используется следующая символика:

,,

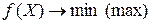где - целевая функция, а - допустимое множество, заданное ограничениями на управляемые переменные.

Если множество управляемых параметров является подмножеством конечномерного пространства, то говорят о конечномерной задаче оптимизации в отличие от бесконечномерных задач, которые являются предметом рассмотрения вариационного исчисления и оптимального управления.

Если целевая функция единственная, то задачу конечномерной оптимизации называют задачей математического программирования, если же критерием оптимальности является требование достижения экстремального значения несколькими функциями управляемых параметров – задачей многокритериальной оптимизации.

Если целевая функция и ограничения задачи математического программирования являются линейными относительно управляющих параметров, то говорят о задаче линейного программирования. При нелинейной зависимости целевой функции или ограничений от управляемых параметров говорят о задаче нелинейного программирования.

Если при линейных ограничениях минимизируемая целевая функция является квадратичной формой, то говорят о задаче квадратичного программирования.

В случае, когда целевая функция является отношением двух линейных функций, а ограничения линейны, имеем задачу дробно-линейного программирования.

Задачи оптимизации, в которых необходимо найти наименьшее значение выпуклой целевой функции на выпуклом множестве, называют задачами выпуклого программирования.

Если множество допустимых управляющих параметров оказывается конечным множеством, то мы имеем задачу дискретного программирования. А если к тому же координаты этих точек – целые числа, то говорят о задаче целочисленного программирования.

Наименование перечисленных задач – «задачи программирования» – связано с тем, что целью решения задач является выбор программы действий.

Задачи математического программирования часто возникают в экономике, при планировании производственных процессов и количественной оценки альтернатив, связанных с принятием управленческих решений. Постановка этих задач обычно основана на анализе и сопоставлении расходуемых ресурсов и полученного результата. Такой подход принято называть методом «затраты - эффективность». Рассмотрим несколько примеров такого подхода.

Транспортная задача

Транспортная задача в ее классической постанове заключается в следующем.

Пусть задано пунктов производства или хранения однородного продукта, в каждой из которых производится или имеется запас, равный . Имеются пунктов потребления или назначения, в которые необходимо завести данный продукт. Задана потребность в продукте для каждого -го пункта потребления - 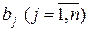. Предположим, что , т.е. что общий объем производства равен общему объему потребления. Задана стоимость перевозки единицы продукции из -го пункта производства в -й пункт потребления.

Требуется определить количество продукции

, (1.1)

перевозимой до каждого - го пункта потребления, так чтобы

1) вывести продукцию всех пунктов производства

(1.2)

2) удовлетворить всех потребителей

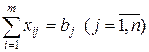(1.3)

3) Суммарная стоимость перевозок

(1.4)

была минимальной.

Получилась задача (1.1-1.4) линейного программирования, так как минимизируемая функция (1.4) и ограничения (1.1) – (1.4) зависят от искомых величин .

Существуют и другие постановки транспортных задач, когда , имеются ограничения на пропускную способность и планируется перевозка неоднородного продукта неоднородным транспортом.

Задача определения оптимальной производственной программы предприятия

Оптимальной производственной программой предприятия считается такая программа (номенклатура и объем выпуска продукции), при которой достигается максимальный экономический эффект. Такая производственная программа может быть определена только путем решения задачи по размещению и концентрации производства по отрасли или народному хозяйству в целом.

При рассмотрении одного предприятия под оптимальной производственной программой следует понимать такой выпуск изделия за определенный промежуток времени, при котором достигается максимальная экономическая эффективность для данного предприятия. Определение такой программы предприятия может быть сведено к следующей задаче математического программирования.

Необходимо найти, какое количество изделий каждого наименования 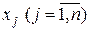должно выпускать за определенный период времени (обычно за год) данное предприятие, чтобы прибыль предприятия

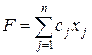
достигла максимального значения при ограничениях

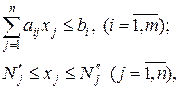(1.5)

где - заданное число наименований изготовляемых на предприятии изделий; - число видов ресурсов, используемых при изготовлении выпускаемых изделий; 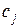- прибыль, получаемая от реализации одного изделия -го наименования; - коэффициент, выражающий потребность (расход) -го ресурса для изготовления одного изделия -го наименования; - имеющееся на предприятии количество ресурса -го вида (); - соответственно нижняя и верхняя границы допустимого количества выпуска продукции -го наименования (устанавливаются путем изучения потребностей и получения заявок предприятием да начала планового периода).

Система неравенств (1.5) означает, что потребность в любом виде ресурсов на изготовление всех наименований за плановый промежуток времени не должна превышать имеющегося количества.

К числу ресурсов, которые могут учитываться при решении задачи, относятся главным образом оборудование и площади основных цехов предприятия, остальные виды лимитирующего сырья, материалов, покупных полуфабрикатов. В некоторых случаях должно учитываться наличие рабочей силы, установленный размер фонда заработной платы и другие виды ресурсов.

Если в неравенстве (1.5) индекс означает некоторую группу оборудования, то будут представлять собой трудоемкость изготовления одного изделия -го наименования на этой группе оборудования за период времени, для которого определяется оптимальная производственная программа.

Задача определения оптимального состава смесей (задача о диете)

Пусть требуется составить смесь из различных видов (материалов), каждый из которых содержит видов веществ (элементов или других составляющих).

Известно количество -го вещества в -м виде сырья и цены на сырье .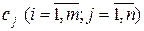

Необходимо составить смесь заданного в определенных пределах состава с наименьшей стоимостью, т.е. требуется найти минимум целевой функции

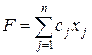
при ограничениях

где - количество сырья -го вида, используемое для составления смеси; 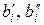- соответственно наименьшее и наибольшее допустимое количество -го вещества в смеси; и имеющееся количество сырья -го вида.

Такие задачи возникают, например, при определении состава горючих, рациона питания животных и т.д.

Контрольные вопросы

1. Какова суть экстремальных задач?

2. Какой раздел методов оптимизации получил название линейного программирования?

3. Дайте понятие объекта оптимизации.

4. Что значит построить математическую модель объекта оптимизации?

5. В чём состоит определение границ объекта оптимизации?

6. Какие величины называют управляемыми переменными?

7. Как вводится понятие целевой функцией?

8. Приведите формулировку математической задачи оптимизации.

9. Какие задачи называют задачами линейного программирования?

10. Какие задачи называют задачами квадратичного и дробно-линейного программирования?

11. В чём состоит особенность задач дискретного и целочисленного программирования?

Дата добавления: 2014-01-06