
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Многомерной минимизации
Основные принципы организации численных методов
Для численного решения задач безусловной минимизации 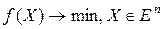 разработано много алгоритмов, использующих итерационные процедуры вида
разработано много алгоритмов, использующих итерационные процедуры вида
 ,
,  , (4.7)
, (4.7)
позволяющие при определенных условиях построить последовательность  такую, что
такую, что
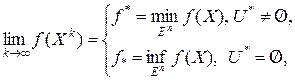 (4.8)
(4.8)
где 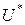 - множество точек глобального минимума функции
- множество точек глобального минимума функции  . Последовательность
. Последовательность  , удовлетворяющая требованию (4.8), называется минимизирующей для функции
, удовлетворяющая требованию (4.8), называется минимизирующей для функции  . Если, кроме того, для случая
. Если, кроме того, для случая  дополнительно выполняется условие
дополнительно выполняется условие
 , (4.9)
, (4.9)
то говорят, что минимизирующая последовательность сходится к множеству 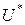 . Если множество
. Если множество 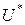 состоит из единственной точки
состоит из единственной точки  , то для сходящейся к
, то для сходящейся к 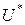 минимизирующей последовательности
минимизирующей последовательности  .
.
Замечание. Минимизирующая последовательность может и не сходиться к точке минимума. Например, для 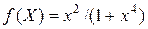 ,
,  , последовательность
, последовательность 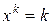 является минимизирующей, но не сходится к единственной точке минимума
является минимизирующей, но не сходится к единственной точке минимума 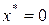 .
.
Среди итерационных процедур (4.7) можно условно выделить такие, которые гарантируют отыскание решения задачи за конечное число итераций (шагов). Однако их удается построить лишь для некоторых специальных типов задач минимизации. Как правило, приходится иметь дело с бесконечными последовательностями  , поэтому говорить о достижении решения можно лишь в пределе.
, поэтому говорить о достижении решения можно лишь в пределе.
Важной характеристикой сходящихся минимизирующих последовательностей является скорость сходимости. Говорят, что последовательность  сходится к точке
сходится к точке  линейно (со скоростью геометрической прогрессии), если существует такое число
линейно (со скоростью геометрической прогрессии), если существует такое число  , что выполняется неравенство
, что выполняется неравенство 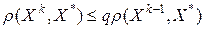 , т.е.
, т.е. 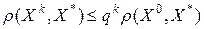 .
.
Сходимость называют сверхлинейной (т.е. более быстрой, чем определяемая любой геометрической прогрессией), если  ,
, 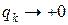 при
при  .
.
Наконец, термин квадратичная сходимость используется, если справедлива оценка 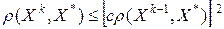 ,
, 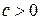 или
или  , где
, где  .
.
Для многих алгоритмов скорость сходимости последовательности  характеризуется и другими неравенствами, например,
характеризуется и другими неравенствами, например,  ,
, 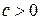 ,
, 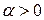 .
.
Установление факта сходимости последовательности  из (4.7) и оценка скорости сходимости дают существенную информацию об итерационном процессе (4.7).
из (4.7) и оценка скорости сходимости дают существенную информацию об итерационном процессе (4.7).
Конкретный вычислительный алгоритм на основе (4.7), в котором может получаться, вообще говоря, бесконечная последовательность  , необходимо дополнять условием остановки (критерием окончания счета). На практике часто пользуются следующими условиями:
, необходимо дополнять условием остановки (критерием окончания счета). На практике часто пользуются следующими условиями:
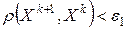 , (4.10)
, (4.10)
 , (4.11)
, (4.11)
 (4.12)
(4.12)
где 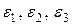 - заранее заданные параметры точности.
- заранее заданные параметры точности.
Ниже будут рассмотрены вычислительные алгоритмы простейших процедур (4.7), как правило, основанные на рекуррентных формулах вида
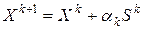 (4.13)
(4.13)
где 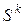 - направление поиска точки
- направление поиска точки 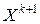 из точки
из точки 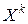 , а число
, а число  - величина шага, которая выбирается так, чтобы выполнялось условие
- величина шага, которая выбирается так, чтобы выполнялось условие
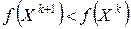 . (4.14)
. (4.14)
Эти алгоритмы различаются способом построения вектора 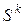 и выбора шага
и выбора шага  .
.
Будем говорить, что в итерационном процессе (4.13) производится исчерпывающий спуск, если величина шага  находится из решения одномерной задачи минимизации
находится из решения одномерной задачи минимизации
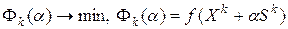 (4.15)
(4.15)
Таким образом, при исчерпывающем спуске на каждом шаге полностью реализуется возможность уменьшить значение целевой функции  при перемещении из точки
при перемещении из точки 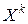 в направлении, коллинеарном вектору
в направлении, коллинеарном вектору 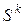 . Величина шага
. Величина шага  может быть найдена, например, с помощью методов одномерной оптимизации.
может быть найдена, например, с помощью методов одномерной оптимизации.
В дальнейшем будет часто использоваться следующее свойство исчерпывающего спуска.
Теорема 4.1. Для дифференцируемой в  функции
функции  в итерационном процессе (4.13) с выбором шага
в итерационном процессе (4.13) с выбором шага  в соответствии с (4.15) для всех
в соответствии с (4.15) для всех  выполняется условие
выполняется условие
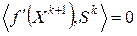 . (4.16)
. (4.16)
Д о к а з а т е л ь с т в о. Запишем необходимое условие минимума функции одной переменной 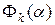 из (4.15), используя правило дифференцирования сложной функции:
из (4.15), используя правило дифференцирования сложной функции:
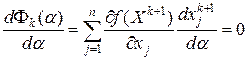 .
.
Учитывая, что  получаем условие (4.16). Дадим геометрическую иллюстрацию соотношения (4.16) в пространстве
получаем условие (4.16). Дадим геометрическую иллюстрацию соотношения (4.16) в пространстве 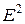 . При перемещении из точки
. При перемещении из точки 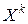 вдоль прямой, задаваемой вектором
вдоль прямой, задаваемой вектором 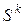 в направлении убывания функции, происходит пересечение линий уровня функции
в направлении убывания функции, происходит пересечение линий уровня функции  до тех пор, пока либо не будет достигнута стационарная точка
до тех пор, пока либо не будет достигнута стационарная точка  , либо прямая не коснется в некоторой точке
, либо прямая не коснется в некоторой точке 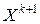 некоторой линии уровня функции
некоторой линии уровня функции  . Равенство (4.16) и есть условие касания (рис. 4.1).
. Равенство (4.16) и есть условие касания (рис. 4.1).
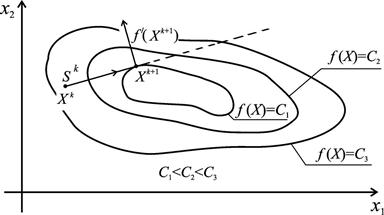
|
Рис. 4.1. Ортогональность направления 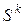 градиенту градиенту 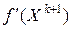 при
исчерпывающем спуске. при
исчерпывающем спуске.
|
Определение 4.1. Направление вектора 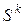 называется направлением убывания функции
называется направлением убывания функции  в точке
в точке 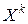 , если при всех достаточно малых положительных
, если при всех достаточно малых положительных 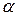 выполняется неравенство
выполняется неравенство 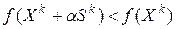 .
.
В итерационном процессе (4.13) используются, как правило, направления убывания. Сформулируем признак направления убывания.
Теорема 4.2. Пусть функция  дифференцируема в точке
дифференцируема в точке 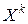 . Если вектор
. Если вектор 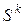 удовлетворяет условию
удовлетворяет условию
 , (4.17)
, (4.17)
то направление вектора 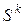 является направлением убывания.
является направлением убывания.
Д о к а з а т е л ь с т в о. Из свойства дифференцируемой функции (4.2) и условия (4.17) следует, что 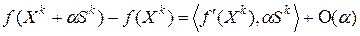 при всех достаточно малых
при всех достаточно малых 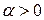 , т.е. вектор
, т.е. вектор 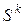 задает направление убывания функции
задает направление убывания функции  в точке
в точке 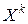 .
.
Геометрически условие (4.17) означает, что вектор 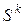 составляет тупой угол с градиентом.
составляет тупой угол с градиентом.
Контрольные вопросы
1. В чём суть задачи многомерной оптимизации?
2. Какая точка называется точкой локального минимума функции многих переменных?
3. Опишите классический метод решения задачи безусловной минимизации функций многих переменных.
4. Дайте определение градиента функции многих переменных и опишите его свойства.
5. Приведите необходимое и достаточное условие минимума функции многих переменных
6. Какие итерационные процедуры используются в алгоритмах численного решения задач безусловной минимизации.
7. Опишите понятие скорости сходимости численного метода оптимизации.
8. Как производится исчерпывающий спуск в итерационной процедуре и каким замечательным свойством он обладает?
9. Опишите понятие направления убывания
10. Какому условию должен удовлетворять вектор, задающий направление убывания?
|
Дата добавления: 2014-01-06; Просмотров: 1385; Нарушение авторских прав?; Мы поможем в написании вашей работы!