Овражный метод

Пусть в задаче безусловной оптимизации (4.1) функция носит овражный характер. Опишем простейший вариант овражного метода.

В начале поиска минимума «овражной функции» задаются две исходные точки , , из которых производят спуск с помощью какого-либо варианта градиентного метода и получают две точки , на «дне оврага». Затем строят новую точку , где – положительная постоянная, называемая овражным шагом. Вообще говоря, точка 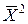будет находиться на “склоне оврага”, поэтому, организовав спуск градиентным методом, получим следующую точку на “дне оврага”. Если таким образом построены точки 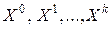, , 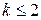то из точки

совершают спуск в следующую точку на «на дне оврага».

Эффективность овражного метода существенно зависит от выбора шага. Если шаг велик, то на крутых поворотах «оврага» точки могут слишком удаляться от «дна оврага» и спуск из точки в точку 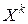может потребовать большого объема вычислений. Кроме того, при больших на крутых поворотах может произойти выброс точки из «оврага», и правильное направление поиска точки минимума будет потеряно. Если же шаг слишком мал, то поиск может замедлиться и эффект от применения овражного метода может стать незначительным.

Скорость сходимости овражного метода может существенно возрасти, если величину овражного шага выбирать переменной, реагирующей на повороты «оврага». При этом желательно за счет увеличения овражного шага по возможности быстрее проходить прямолинейные участки на «дне оврага» на крутых поворотах «оврага» избежать выброса из «оврага» за счет уменьшения овражного шага. Кроме того, желательно добиться по возможности меньшего отклонения точек от «дна оврага» и тем самым сократить объем вычислений, требуемый на градиентный спуск из точки в точку . Интуитивно ясно, что для правильной реакции на поворот «оврага» надо учитывать «кривизну дна оврага», причем информацию о «кривизне» желательно получать из результатов предыдущих итераций овражного метода.

Был предложен следующий способ выбрать овражного шага

, , (6.11)

где 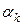- угол между векторам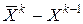и и 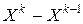, определяемый условием

,

а постоянная 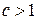является параметром алгоритма. Точка тогда определяется так:

.

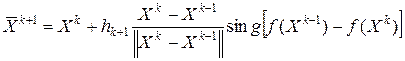Разность в равенстве (6.11) связана с «кривизной дна оврага» и, кроме того, указывает направление изменения «кривизны». В самом деле, при переходе с участков «дна оврага» малой «кривизны» на участки с большей «кривизной» будем иметь . Тогда в силу (6.11) , т.е. овражный шаг уменьшается, приспосабливается к повороту «дна оврага», что в свою очередь приводит к уменьшению выброса точки на «склон оврага». При переходе с участков «дна оврага» большой кривизны на участки с меньшей «кривизной», наоборот, , поэтому овражный шаг увеличится и появится возможность сравнительно быстро пройти участок с малой «кривизной», в частности, прямолинейные участки на «дне оврага». Если «кривизна дна оврага» на некоторых участках остается постоянной, то разность будет близка к нулю, и поиск минимума на таких участках будет проводиться с почти постоянным шагом, сформированным с учетом величины «кривизны» при выходе на рассматриваемый участок.

Параметр 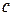в равенстве (6.11) регулирует «чувствительность» метода к изменению «кривизны дна оврага». Правильный выбор этого параметра во многом определяет скорость движения по «оврагу».

Контрольные вопросы

1. Перечислите основные методы, использующие производные; укажите их достоинства и недостатки.

2. Дайте определение градиента функции многих переменных; как ориентирован относительно него любой вектор, задающий направление убывания функции?

3. Какие методы объединяются под названием градиентных методов.

4. Какая итерационная процедура лежит в основе градиентных методов?

5. Как выбирается длина шага в методе градиентного спуска?

6. Приведите описание алгоритма метода градиентного спуска?

7. Как осуществляется исчерпывающий спуск в направлении убывания?

8. Приведите описание алгоритма метода наискорейшего спуска?

9. Поясните геометрический смысл градиентных процедур.

10. В каком случае целесообразно использование овражного метода?

11. Опишите метод минимизации овражных функций.

Дата добавления: 2014-01-06