Множество истинности предикатов

Способа задания предиката

Понятие предиката

Понятие ``предикат'' обобщает понятие ``высказывание''. Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.

Пример предикатов. Возьмём высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для Сократа и Платона.

Возьмём высказывание: ``расстояние от Иркутска до Москвы 5 тысяч километров''. Вместо него мы можем записать предикат ``расстояние'' (означающий, что первый и второй аргумент этого предиката находятся на расстоянии, равном третьему аргументу) для аргументов ``Иркутск'', ``Москва'' и ``5 тысяч километров''.

Пример рассуждения, не выразимого в логике высказываний. Все люди смертны. Сократ - человек. Следовательно, Сократ смертен.

Это рассуждение на языке логики высказываний можно записать тремя отдельными высказываниями. Однако никакой связи между ними установить не удастся. На языке логики предикатов эти предложения можно выразить с помощью двух предикатов: ``быть человеком'' и ``быть смертным''. Первое предложение устанавливает связь между этими предикатами.

1) Высказывательной формой, т. е. следует задать высказывательную форму и множество объектов для переменных

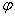(x) = < x - нечетное>, M _x = N

2) Табличный

Табличный способ применяется тогда, когда мало переменных (от 1 до 3), от которых зависит предикат и множество объектов, на котором задан данный предикат невелико.

N-местная высказывательная форма - высказывательная форма, зависящая от N переменных.

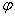(x) = < x > 1>, M _x = R - одноместная высказывательная форма

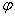(x, y, z) = x + y - z = 10, M _x = M _y = M _z = R - трехместная высказывательная форма

Если поменять порядок следования переменных в предикате, то это будет другой предикат. Если порядок следования не задан, то берётся по алфавиту, а потом по индексам (возрастание).

Если при каком-то значении переменной высказывательная форма, не имеющая знаков логических операций, теряет смысл, то её принято считать ложной.

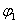(x) = - истина при x < 0

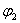(x) = - ложь при x < 0

Упорядоченная n-ка - совокупность n не обязательно различных объектов вместе с заданным порядком их расположения.

{а; п; е; л; ь; с; и; н} = {с; п; а; н; и; е; л; ь} - для множества

(а; п; е; л; ь; с; и; н) ≠ (с; п; а; н; и; е; л; ь) - для упорядоченной n-ки

Декартово произведение (произведение n множеств) - такое множество упорядоченных n-ок, в которых на 1-ом месте объект из 1-ого множества, на 2-ом из 2-ого:

Пусть M _x = {a; b; c}, M _y = {1; 2}, тогда их декартово произведение равно:

M _x * M _y = {(a; 1); (b; 2); (a; 2); (c; 1); (c; 2); (b; 1)}

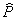(<пэ с крышкой>) - множество истинности предикатов, множество тех значений x, при которых предикат принимает значение <истина>.

Если предикат зависит от двух переменных, то множеством истинности будет множество пар, в которых на 1-ом месте объект из M _x, на втором - из M _y.

Если 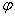(x, y) = < x > y >, M _x = {1; 2; 3), то 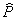= {(3; 1); (3; 2); (2; 1)}

Если множество 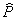совпадает с множеством, на котором задан данный предикат, то предикат называется тождественно истинным.

Если множество 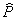пустое, то предикат называется тождественно ложным.

Равносильность высказывательных форм

Высказывательная форма 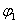равносильна высказывательной форме 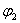, если переменные принимают значение из одного и того же множества и при любом наборе переменных высказывательные формы принимают одинаковые значения истинности.

Равносильные:

x + 1 = 0 <=> x = cos π

| x | > 3 <=> x² - 90 > 0

| x | < 0 <=> sin x = 2

x = 1 <=> x + y - y = 1

Неравносильные:

x > 0 <≠> y > 0

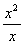x = x <≠> = x

Дата добавления: 2014-01-06