Отыскание минимума линейной функции

При определении минимума линейной функции Z возможны два варианта:

1) отыскать максимум функции F, считая 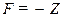и учитывая, что ;

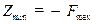2) модифицировать симплексный метод, для этого на каждом шаге следует уменьшать линейную функцию за счет той неосновной переменной, которая входит в выражение линейной функции с отрицательным коэффициентом.

Критерий оптимальности полученного решения в этом случае можно сформулировать следующим образом:

Если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то найденное решение задачи отыскания минимума линейной функции является оптимальным.

Пример 3. Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 фунта азотных, 4 фунта фосфорных и 1 фунт калийных удобрений, а в улучшенный - 2 фунта азотных, 6 фунтов фосфорных и 3 фунта калийных удобрений. Известно, что для хорошего роста растений на некотором газоне требуется по меньшей мере 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3 доллара, а улучшенный - 4 доллара. Определить количество наборов удобрений (х₁ и х₂), которые нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость.

Решение. Построим математическую модель задачи.

Найти значения переменных х₁, х₂, удовлетворяющие условиям:

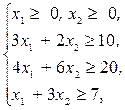(2.11)

при которых целевая функция 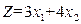принимает минимальное значение.

Решение будем проводить симплексным методом.

Приведем систему к каноническому виду введением дополнительных переменных: ,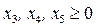

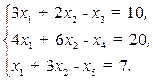(2.12)

В качестве базисных переменных выберем дополнительные переменные 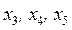. Выразим основные переменные через неосновные:

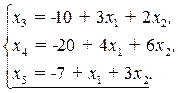(2.13)

Полагая неосновные переменные равными нулю, получаем недопустимое первоначальное базисное решение: 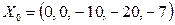. Целевая функция на недопустимом решении не рассматривается!

Для того чтобы решение стало допустимым, необходимо увеличить значение той из неосновных переменных, коэффициенты при которой в выражениях для базисных переменных, принимающих недопустимые значения, положительны. Рассмотрим переменную х₁.

Вычислим для нее оценочные отношения: 10/3, 5, 7. Если увеличить значение переменной х₁ до максимального из указанных значений, то получится допустимое базисное решение, т.к. все переменные станут неотрицательными. Соответствующее уравнение (подчеркнутое) является разрешающим. Таким образом, в новый базис вместо переменной х₅ вводится переменная х₁. Разрешая уравнение относительно х₁. и подставляя в остальные уравнения, получаем:

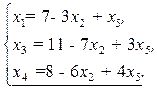(2.14)

Полученное решение допустимое: 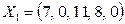. Целевая функция 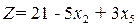_. На полученном решении 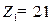. Значение целевой функции может быть уменьшено за счет увеличения значения переменной х₂, так как эта переменная входит в линейную целевую функцию с отрицательным коэффициентом.

Вычислим оценочные отношения для переменной х₂ в тех уравнениях, где коэффициент при х₂ отрицателен: 7/3, 11/7, 8/6. Наименьшее из этих отношений 8/6=4/3 определяет разрешающее уравнение. Итак, в новый базис вместо переменной х₄ вводится переменная х₂. Выразим х₂ и подставим полученное выражение в остальные уравнения и в целевую функцию:

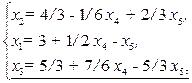(2.15)

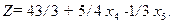(2.16)

Полученное решение допустимое: 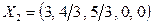. При этом целевая функция 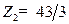. Значение целевой функции может быть уменьшено за счет увеличения значения переменной х₅, так как эта переменная входит в линейную целевую функцию с отрицательным коэффициентом.

Вычислим оценочные отношения для переменной х₅ в тех уравнениях, где коэффициент при х₅ отрицателен: 3, 1. В первом уравнении оценочное отношение равно ∞, т.к. коэффициент при х₅ положительный и уравнение не ограничивает рост переменной. Наименьшее из этих отношений определяет разрешающее уравнение. Итак, в новый базис вместо переменной х₃ вводится переменная х₅. Выразим х₅ и подставим полученное выражение в остальные уравнения и в целевую функцию:

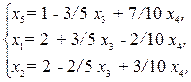(2.17)

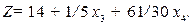(2.18)

Полученное решение допустимое: 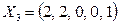. При этом целевая функция 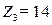. Значение целевой функции не может быть уменьшено, так как все неосновные переменные входят в линейную целевую функцию с неотрицательными (положительными) коэффициентами. Следовательно, найденное решение является оптимальным.

Дата добавления: 2014-01-06