
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Двойственные задачи
|
|
|
|
Метод искусственного базиса (М-метод)
Чтобы избежать затруднений при нахождении первоначального базисного решения, применяют метод искусственного базиса. Алгоритм метода содержит следующие шаги:
1. Привести ЗЛП к каноническому виду.
2. Построить М-задачу. Для этого в каждое уравнение системы ограничений, не имеющее переменной, исключенной из других уравнений, необходимо ввести искусственную переменную с коэффициентом 1, не меняя знака равенства. Искусственные переменные также вводятся в целевую функцию с коэффициентом –М (если решается задача на максимум) или +М (если решается задача на минимум), где М – сколь угодно большое число.
3. Выписать исходное базисное решение.
4. Решить М-задачу симплексным методом. При решении учесть следующие возможные случаи:
а) если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующее решение исходной задачи является оптимальным и экстремумы целевых функций равны;
б) если в оптимальном решении М-задачи хотя бы одна из искусственных переменных не равна 0, то исходная задача не имеет оптимального решения из-за несовместимости системы ограничений;
в) если М-задача не имеет оптимального решения, то исходная задача также не имеет оптимального решения.
Если в процессе решения искусственная переменная выводится из базиса, то можно исключить ее из дальнейших расчетов.
Пример 8. Найти наибольшее значение функции 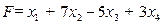 при ограничениях:
при ограничениях:
 (2.29)
(2.29)
Задача дана в каноническом виде. Составим М-задачу, для этого введем в первое уравнение переменную х5, во второе – переменную х6, в целевую функцию добавим – М х5 – М х6.
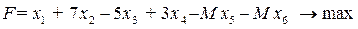 (2.30)
(2.30)
 (2.31)
(2.31)
Первоначальный базис х5, х6. Решаем задачу симплексным методом.
|
|
|
 (2.32)
(2.32)
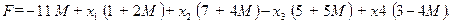 (2.33)
(2.33)
Решение допустимое  . Переведем в базис переменную х 2, входящую в целевую функцию с положительным коэффициентом. Оценочные отношения для переменной х2 равны 2 и 5. Первое уравнение системы является разрешающим. Новый базис х2, х6. Т.к. искусственная переменная х5 выведена из базиса, не учитываем ее в дальнейших вычислениях. Система ограничений и целевая функция принимают вид:
. Переведем в базис переменную х 2, входящую в целевую функцию с положительным коэффициентом. Оценочные отношения для переменной х2 равны 2 и 5. Первое уравнение системы является разрешающим. Новый базис х2, х6. Т.к. искусственная переменная х5 выведена из базиса, не учитываем ее в дальнейших вычислениях. Система ограничений и целевая функция принимают вид:
 (2.34)
(2.34)
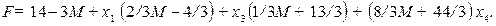 (2.35)
(2.35)
Решение 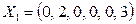 . Целевая функция
. Целевая функция  .
.
Переведем в базис переменную х3, выражая её из второго уравнения. Новый базис х2, х3. Т.к. переменная х6 выведена из базиса, исключаем ее из дальнейшего решения.
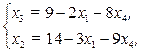 (2.36)
(2.36)
 . (2.37)
. (2.37)
Выполнен критерий оптимальности решения задачи на максимум целевой функции. Оптимальное решение 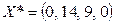 , максимальное значение целевой функции
, максимальное значение целевой функции 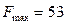 .
.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной, или сопряженной по отношению к исходной. Понятие двойственности взаимно. Теория двойственности позволяет провести полезные качественные исследования задач линейного программирования. В зависимости от вида исходной задачи различают симметричную, несимметричную и смешанные пары двойственных задач.
Пара двойственных задач называется симметричной, если одна из задач задана в стандартной форме (двойственная задача также запишется в стандартной форме).
Пара двойственных задач называется несимметричной, если одна из них задана в канонической форме и переменные неотрицательны или одна из задач задана в неканонической форме и переменные произвольны по знаку.
Когда система ограничений одной из задач содержит как уравнения, так и неравенства, и некоторые переменные неотрицательны, то пара двойственных задач называется смешанной.
Рассмотрим правила составления двойственных задач.
Симметричная пара
1. В исходной задаче знаки неравенств системы m ограничений приводятся к единому виду: «≤» в задаче на максимум и «≥» в задаче на минимум.
|
|
|
2. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная yi, i =1, 2, … m.
3. Составляется целевая функция Z от переменных yi (i =1, 2, … m), коэффициентами которой будут свободные члены системы ограничений исходной задачи. Цель меняется на противоположную.
4. Составляется система ограничений двойственной задачи. Матрицу коэффициентов системы ограничений двойственной задачи получают транспонированием матрицы коэффициентов исходной задачи. Знаки неравенств системы ограничений двойственной задачи противоположны знакам неравенств в исходной задаче. Свободными членами неравенств системы ограничений являются коэффициенты целевой функции исходной задачи. Переменные yi (i =1, 2, … m) неотрицательны.
В таблице 2.2 показано соответствие задач симметричной пары.
Таблица 2.2. Соответствие стандартных взаимно-двойственных задач
| Исходная задача | Двойственная задача |
 (2.38) (2.38)
| 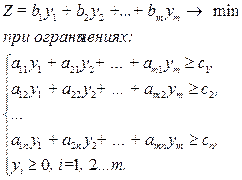 (2.39) (2.39)
|
Несимметричная пара
1. Если система ограничений исходной задачи состоит из уравнений, то соответствующие им двойственные переменные произвольны по знаку.
2. Если переменные xj (j=1, 2, …n) исходной задачи неотрицательны, то ограничения двойственной задачи имеют вид неравенств со знаком «≤» для задачи на максимум и «≥» для задачи на минимум.
3. Далее построение двойственной задачи выполняется как для симметричной пары.
В таблице 2.3 показано соответствие задач несимметричной пары.
Таблица 2.3. Соответствие задач несимметричной пары
| Исходная задача | Двойственная задача |
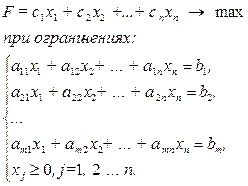 (2.40) (2.40)
| 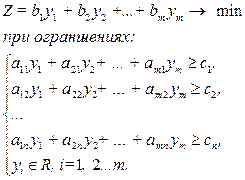 (2.41) (2.41)
|
 (2.42) (2.42)
| 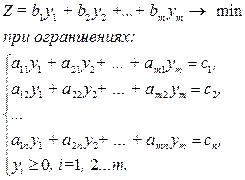 (2.43) (2.43)
|
Смешанная пара
1. Если система ограничений исходной задачи содержит как уравнения, так и неравенства, то при построении двойственной задачи придерживаются следующего правила. Если двойственная переменная поставлена в соответствие ограничению-неравенству, то она неотрицательна, если уравнению, то переменная произвольна по знаку.
2. Если переменная исходной задачи неотрицательна, то ей ставится в соответствие ограничение–неравенство, если переменная произвольна по знаку, то соответствующее ей ограничение является уравнением.
3. Далее построение двойственной задачи выполняется как для симметричной пары.
|
|
|
В таблице 2.4 показано соответствие задач смешанной пары.
Таблица 2.4. Соответствие смешанных взаимно-двойственных задач
| Исходная задача | Двойственная задача |
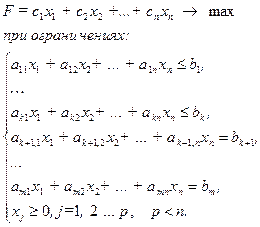 (2.44)
(2.44)
|  (2.45)
(2.45)
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 869; Нарушение авторских прав?; Мы поможем в написании вашей работы!