
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Циклические программы
|
|
|
|
Циклом называется процедура, в которой вычислительные операции выполняются многократно заданное число раз или до достижения некоторой переменной, вычисляемой в теле цикла, определенного, наперед заданного значения.
Понятие о циклах и их классификации приведено в разделе 8.2.
Циклы могут быть организованы с использованием оператора IF или с использованием специальных операторов: FOR/NEXT, WHILE/WEND, DO/LOOP. Примеры организации циклов приведены в табл. 9.4.2.
Оператор FOR/NEXT
Оператор FORслужит для организации циклов с заданным числом повторений. Цикл относится к циклам с постусловием. Формат оператора:
FOR i=Iнач TO iкон STEP di
<тело цикла>
Next i
В данном формате Iнач – начальное значение переменной цикла, Iкон – конечное значение переменной цикла, а di – шаг приращения значения переменной цикла.
Операторы FOR и NEXT образуют операторные скобки, между которыми заключено тело цикла.
Пример 9.4.8. Напечатать таблицу перевода температуры из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) для значений температуры от 15оС до 30оС с шагом 1оС. Формула перевода: F=1,8С+32.
| Таблица 9.4.2 | |
| а) цикл с постусловием REM использование для организации цикла REM оператора IF i=iнач: REM заголовок цикла M1: <тело цикла, вычисление функции F(i)> i=i+di IF i<=iкон THEN GOTO M1: REM конец цикла PRINT "Результат"; F ----------------------------------------------------- REM использование оператора FOR/NEXT FOR i=iнач TO N STEP di <тело цикла, вычисление функции F(i)> NEXT i PRINT "Результат";F |
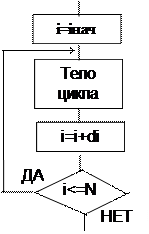 Схема алгоритма Схема алгоритма
|
| б) цикл с предусловием REM Использование оператора IF F=<выражение> i=iнач M1: IF F<=e THEN GOTO M2 <тело цикла, вычисление F(i)> i=i+di GOTO M1 M2: PRINT "Результат"; F ---------------------------------------------------- REM Использование оператора REM WHILE/WEND F=<выражение> i=iнач WHILE F>e <тело цикла, вычисление F(i)> i=i+di WEND PRINT "Результат";F |
Схема алгоритма

|
|
|
|
Решение. Число шагов в задаче известно, поэтому для решения задачи применим оператор FOR/NEXT. Переменная цикла целочисленная, изменяется с шагом 1.
INPUT "Введите начальное значение температуры о С: ", tN
INPUT "Введите Конечное значение температуры о С: ", tK
INPUT "Укажите шаг изменения температуры о С: ", dT
PRINT Tab(10);"To C"; Tab(20);"To F"
FOR i = tN TO tK STEP dT
F= 1.8*i+32
PRINT Tab(10);i; Tab(20); y
NEXT i
END
Пример 9.4.9. Вычислить многочлен P(x) = 5x3 + 2x2 –15x – 6 при х = 2,5
Решение. Задачу можно решить что называется "в лоб" – записать выражение по правилам языка Бейсика – и дело сделано. Однако для повышения скорости вычисления целесообразно заменить операции умножения операциями сложения и вычитания. Особенно это актуально в управляющих ЭВМ, работающих в реальном масштабе времени.
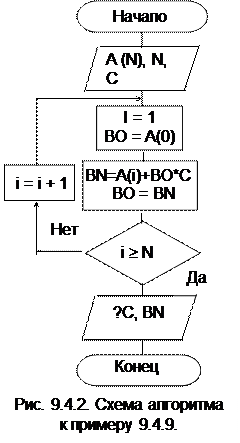 Для вычисления многочлена используется схема Горнера (рис.9.4.2.).
Для вычисления многочлена используется схема Горнера (рис.9.4.2.).
Пусть задан многочлен:
Р(х) = а0 хn + а1 хn-1 +... + аn-1 х + an (9.4.6)
Требуется вычислить значение многочлена при х = с, т.е.
Р(с) = а0 сn + а1 сn-1 +... + аn-1 с + an
Запишем эту формулу в виде:
Р(с) = (...((а0 с+ а1) с + а2) с + a3) с +...+ an-1) с+ an
Введем вспомогательную переменную b:
b0 = a0
b1 = a1 + k1 , k1 = b0 c
b2 = a2 + k2 , k2 = b1 c
...
bn = an + kn , kn = bn-1 c.
Отсюда bn = Р(с).
Таким образом, вычисление значения многочлена Р(х) при х = с сводится к повторению элементарных операций:
ki = bn-1 c, bi = ai + ki , (i = 1,2,..., n), где b0 = a0.
Вычисление многочлена Р(х) при х = с обычно осуществляется по схеме, известной как схема Горнера. В общем виде:
 a0 a1 a2 ... an
+
с b0c b1c... bn-1c
b0 b1 b2 ... bn = P (c)
a0 a1 a2 ... an
+
с b0c b1c... bn-1c
b0 b1 b2 ... bn = P (c)
|
В числовом выражении:
 5 2 -15 -6
2,5 +
12,5 36, 25 53, 125
5 14,5 21,25 47,125 = Р(2,5) 5 2 -15 -6
2,5 +
12,5 36, 25 53, 125
5 14,5 21,25 47,125 = Р(2,5)
|
То есть Р(2.5) = 47,125
Схема алгоритма вычисления многочлена по схеме Горнера приведена на рис. 9.4.2, где
А(N) – вектор коэффициентов многочлена, N – степень многочлена, С – значение аргумента, ВО – коэффициент bi, BN – текущее значение многочлена.
|
|
|
Оператор WHILE/WEND
Оператор WHILEслужит для организации циклов с заданным числом повторений, относится к циклам с постусловием. Условием окончания цикла является достижение функцией, вычисляемой в теле цикла, заданного значения. Формат оператора:
WHILE <условие>
<тело цикла>
WEND
Тело цикла выполняется в том случае, когда условие истинно. Если условие ложно, то программа выходит из цикла. Особенностью использования данного цикла является то, что значение вычисляемой функции должно быть известно перед входом в цикл. Если начальное значение функции меньше заданной величины e, то программа не войдет в цикл.
Оператор DO - универсальный оператор, служит для организации циклов типа "ПОКА". Он может быть организован как цикл с предусловием, так и как цикл с постусловием. Когда в теле цикла используется оператор WHILE, то тело цикла выполняется в том случае, если условие истинно. Когда используется оператор UNTIL, то тело цикла выполняется в том случае, если условие ложно.
Оператор DO
а) цикл с предусловием б) цикл с постусловием
DO <WHILE|UNTIL> DO
<тело цикла> <тело цикла>
LOOP LOOP <WHILE|UNTIL>
Пример 9.4.10. Вычислить площадь фигуры ограниченной прямыми Xn=a, Xk =b, y=0 и графиком функции y=ex+5Sin(x) c точностью E.
Решение. Площадь фигуры может быть вычислена с помощью определенного интеграла. Для вычисления определенного интеграла численными методами необходимо организовать цикл типа "ДО", а чтобы вычислить интеграл с заданной точностью применяется метод двойного прохода и реализуется эта процедура с помощью цикла "Пока".
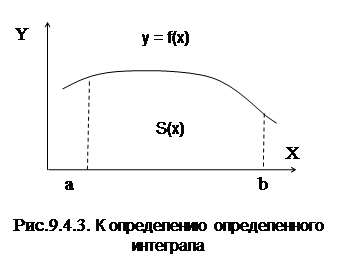
Вычисление определенного интеграла
Пусть функция у = f (x) не отрицательна и непрерывна на отрезке [а; b]. Тогда площадь S (x) переменной криволинейной трапеции представляет собой функцию от х (рис. 9.4.3).
Производная от S (x) равна f (x) всюду на отрезке [а; b]. Иными словами, S (x) оказывается первообразной для f (x).
Процедура нахождения первообразной S (x) от функции f (x) называется интегрированием.
Приращение любой первообразной для функции f (x), получаемое при переходе от а к b, называется определенным интегралом функции f (x), взятым в пределах от а к b, и обозначается символом 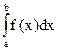 . Здесь а и b называют соответственно нижним и верхним пределами интегрирования.
. Здесь а и b называют соответственно нижним и верхним пределами интегрирования.
|
|
|
С геометрической точки зрения определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной графиком функции f (x), прямыми х = а, х = b и осью х (рис. 9.4.3):
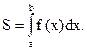 (9.4.7)
(9.4.7)
По определению
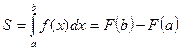 ,
,
где F(b) и F(а) — первообразные для функции f(x) при х = b и х = а соответственно. Для большинства функций первообразную f(x) не удается выразить через элементарные функции, поэтому чаще интеграл вычисляют численными методами.
Сущность метода численного интегрирования состоит в том, что отрезок интегрирования [а; b] разбивают на п элементарных отрезков [xi-1, хi] и заменяют интеграл функции f(x) суммой прямоугольников Si = f(ti) xi (рис. 9.4.4), где f(ti) — значение функции в некоторой точке (ti) внутри i-го отрезка; D хi — длина отрезка, D хi, = хi - xi-1, то есть
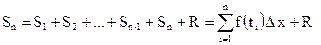 (9.4.8)
(9.4.8)
Здесь Sn - интегральная сумма, R - погрешность усечения. Предел этой суммы при неограниченном увеличении числа отрезков разбиения, когда длина наибольшего из элементарных отрезков D xi стремится к нулю, есть интеграл от функции f (x) на отрезке [а; b]:
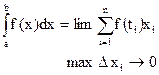
Простейший метод численного интегрирования — метод средних прямоугольников. В нем используется замена интеграла интегральной функцией (9.4.4). В этом случае все отрезки D xi равны между собой, а в качестве f(ti) принимается значение функции в середине отрезка:
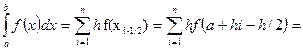
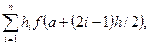
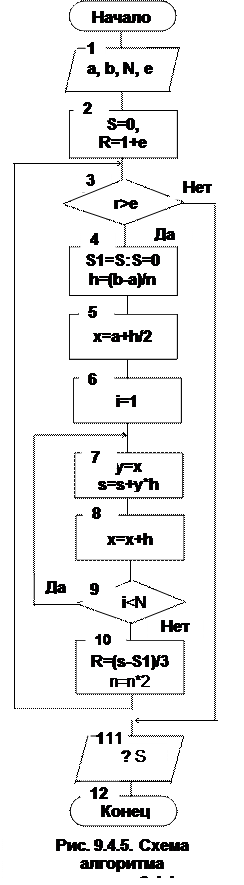
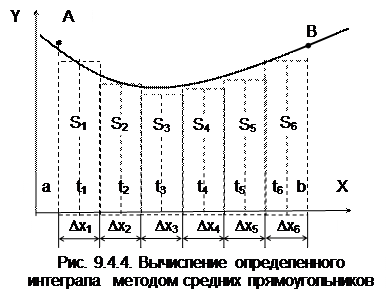 где h — длина элементарного отрезка, h = (b-а) / п; xi-1/2 — значение аргумента в середине i -го отрезка, xi-1/2 = а + (2i - 1)(b - а)/(2п) Схема алгоритма приведена на рис. 9.4.5..
где h — длина элементарного отрезка, h = (b-а) / п; xi-1/2 — значение аргумента в середине i -го отрезка, xi-1/2 = а + (2i - 1)(b - а)/(2п) Схема алгоритма приведена на рис. 9.4.5..
В других методах вычисляют не площадь прямоугольника, а площадь криволинейной трапеции, заменяя функцию f(x) на элементарном отрезке интерполирующей функцией. Если в качестве интерполирующей функции используется линейная функция, то получаем метод трапеций:
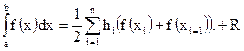 (9.4.9)
(9.4.9)
В зависимости от используемой интерполирующей функции различают методы Ньютона, Симпсона, Ромберга. В методе Симпсона, например, в качестве интерполирующей функции используется многочлен второй степени ax2 + bх + с. Эти методы обеспечивают получение более точных результатов при меньшем числе шагов.
|
|
|
Формула трапеций (9.4.9) после преобразования принимает вид:
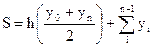 , (9.4.10)
, (9.4.10)
а формула Симпсона записывается следующим образом:
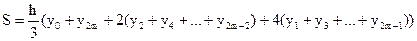 (9.4.11)
(9.4.11)
Программа вычисления определенного интеграла методом средних прямоугольников c заданной точностью:
Программа содержит два вложенных цикла: цикл For/Next и цикл While/wend. Первый цикл – внутренний, он обеспечивает вычисление площади криволинейной трапеции при заданном числе отрезков разбиения. Второй цикл – внешний, этот цикл обеспечивает достижение заданной точности. Для достижения заданной точности используется метод двойного прохода. Суть этого метода состоит в следующем. Вычисляется площадь криволинейной трапеции при заданном числе отрезков разбиения и результат запоминается. Затем увеличивают число отрезков разбиения вдвое и снова вычисляют площадь криволинейной трапеции. После этого вычисляют ошибку интегрирования по приближенной формуле. Процесс вычисления заканчивается, когда ошибка интегрирования станет меньше или равной некоторой наперед заданной величине.
 INPUT "Введите границы отрезка интегрирования _ а и b "; a, b
INPUT "Введите границы отрезка интегрирования _ а и b "; a, b
INPUT "Укажите число отрезков разбиения N ", N
INPUT "Укажите требуемую точность, е ", e
s = 0: r = 1 + e
WHILE r > e
s1 = s: s = 0
h = (b - a) / N
x = a + h / 2
FOR i = 1 TO N
y = f(x)
s = s + y * h
x = x + h
NEXT i
r = ABS(s - s1) / 3
N = N * 2
WEND
PRINT "S="; s
END
В программе обозначено: S – площадь фигуры на текущем шаге, S1 - площадь фигуры на предыдущем шаге, R – погрешность усечения.
Оценка погрешности усечения осущест-вляется по сложным формулам, однако для практических целей можно воспользоваться приближенными формулами (принцип Рунге):
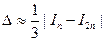 - для формулы трапеции (9.4.12)
- для формулы трапеции (9.4.12)
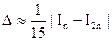 - для формулы Симпсона.
- для формулы Симпсона.
(9.4.13)
Здесь In – значение интеграла при разбиении отрезка интегрирования на n частей, а I2n - значение интеграла при разбиении отрезка на 2n частей.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1388; Нарушение авторских прав?; Мы поможем в написании вашей работы!