Метод дихотомии (деления отрезка пополам)

Уточнение значения корня на отрезках отделения

Уточнение значений корней на отрезках отделения осуществляется различными методами одномерной поисковой оптимизации: деления отрезка пополам, простых итераций, касательных и др.

При выборе метода следует исходить из:

а) сложности подготовки задачи к решению;

б) быстродействия алгоритма;

в) времени и точности решения задачи.

Рассмотрим некоторые методы.

Достоинством метода является его простота, а также то, что этот метод не накладывает никаких ограничений на исследуемую функцию. Достаточно, чтобы на данном отрезке был корень и притом только один.

Суть метода состоит в следующем. Отрезок отделе­ния корня [а; b] делят пополам и точку деления с принимают за значение корня. Сразу же проверяют, если значение функции в точке с станет меньше или равно требуемой точность вычисления значения функции, или длина отрезка [a, с] станет меньше требуемой точности уточнения значения корня, то точка c принимается за значение корня и процесс поиска корня заканчивается. В противном случае определяют, на каком из отрезков [а;с] или [с; b] функция меняет знак и выбирают его для последующего анализа. Если F(a)*F(c)<0, то корень находится слева от точки С, в ином случае корень находится справа от точки С. Пусть F(a)*F(c)<0, то есть корень лежит на отрезке [а; с]. Тогда точку В переносят в точку С, то есть В=С и этот отрезок снова делят пополам и так далее. Каждый раз корень уравнения оказывается локализованным на все меньшем и меньшем отрезке. Процесс поиска корня заканчивается, когда длина отрезка [а; b] станет меньше или равна заданной точности уточнения корня e или значение функции в точке c станет меньше или равно требуемой точности вычисления значения функции в этой точке. Метод всегда обеспечивает сходимость процесса, то есть последовательность приближенных значений корня с₁ ,с₂, с₃,...,с_n будет сходиться к самому значению корня с. Алгоритм уточнения значения корня на отрезке отделения методом деления отрезка пополам приведен на рис. 9.4.7.

Метод итераций.

В данном методе требуется задать начальное приближение х₀ на отрезке отделения корня [ а; b ], выб­рать шаг изменения переменной D х и последовательно решать уравнение вида:

x = j (x), (9.4.14)

полученное путем эквивалентных преобразований из исходного уравнения f(x) = 0. В результате решения этого уравнения получаем ряд приближений корня:

x_k+1=j(х_k), k=0,1,2,(9.4.15)

Процесс уточнения корня прекращается, когда вы­полняется условие

|x_k+1 - (x_k)| <e или f(x_k+1)< e (9.4.16)

Время поиска зависит от выбранного начального приближения х₀ и шага D х.

Выражение вида (9.4.14) называется рекуррентной формулой. В итерационных алгоритмах рекуррентная формула имеет вид

x_i+1 = j (x_i). (9.4.17)

Пример 9.4.12. Пусть дано уравнение x cos (x) - ln(x + 1,1) = 0

Требуется уточнить корни уравнения на от­резке [ а; b ] с точностью до e = 0,01.

Решение. Преобразуем уравнение к виду (9.4.14)

x cos(x)=ln(x+1,1) (9.4.18)

Представим выражение (9.4.18) в виде, удобном для использования в итерационном цикле:

(9.4.19)

Алгоритм итерационного цикла представляет собой обычный цикл типа "Пока" и может быть реализован как цикл с предусловием или как цикл с постусловием.

Метод касательных (метод Ньютона). Пусть на отрезке [a; b] отделен корень с уравнения f (x) = 0 и f(x) — функция, непрерывная на отрезке [а; b], и на интервале ]а; b[ существуют отличные от нуля производные f’ и f`”.

Так как f’ (x) ¹ 0, то запишем уравнение f (x) = 0 в виде:

(9.4.20)

Решаем его методом итераций. Имеем

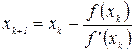(9.4.21)

Если на отрезке [a; b] f'(x)f" (х) > 0, то нулевое приближение корня выбираем в точке b: х₀ = b, если же f'(x)f" (х) < 0, то нулевое приближение выбираем в точке a: х₀ = а..

Построим график функции у = f (x). Пусть для опре­деленности f’ (х) > 0 и f" (х) > 0, то есть функция вог­нутая (рис. 9.4.8). Проведем касательную к графику фун­кции в точке В (b, f (b)). Ее уравнение будет иметь вид:

y = f (b) + f'(b) (х - b).

Найдем точку пересечения касательной с осью х (точка b₁). Так как в этой точке у=0, то, решая уравнение относительно х, получим:

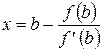. (9.4.22)

Это и есть первое приближение решения уравнения - x₁.

Проведем касательную к графику функции в точке b₁ (x₁; f(x₁)). Найдем точку пересечения касательной с осью х.

(9.4.23)

Для произвольной точки i получим

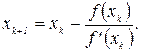(9.4.24)

Отношение f(x_i)/ f '(x_i) есть не что иное, как приращение значения аргумента Dх_i. Действительно, так как f '(x_i) численно равно тангенсу угла наклона касательной к графику функции f'(x_i) = tg(a) = Bb/bb₁, то

x₀ – x₁ =bb₁= Bb₁/tg(a).

На каждом шаге значение Dх_i меняется.

Таким образом формула (9.4.24) дает последовательность приближений (х_i ) корня.

Метод наискорейшего спуска. Пусть дано f (x) = 0. Функция дважды дифференцируемая. Начальное приближение х₀. Очередное приближение вычисляется по формуле:

x_i+1 = x_i + l_in_i, (9.4.25)

где n_i — направление поиска: n_i = f'(x); l_i - шаг: l_i = (f' (x_i))² / f"(x_i).

Поиск прекращается, когда будет выполнено усло­вие x_i+1 - x_i < e, где e — требуемая точность поиска корня.

Недостатками методов касательной и наискорейше­го спуска является необходимость нахождения производных.

Дата добавления: 2014-01-06