Числа конечной точности

Целые числа в математике и их аналоги в n-разрядных арифметиках тождественны (по количеству) в рамках их представления с этой разрядностью. При этом можно отметить основные отличия представления чисел в поле памяти человека и в поле памяти n-разрядной арифметики:

бесконечное и счетное множество целых чисел представляется отрезком [–N; +N], где N – максимальное число, представимое в этой арифметике (многоточие – общее число единиц, равное n): N = (111... 1)2;

бесконечное и несчетное множество действительных чисел
(-¥;+¥), располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);

нуль во множестве действительных чисел в любой своей окрестности имеет множество чисел, а нуль в n-разрядной арифметике представлен изолированно.

Все вычисления в цифровых вычислительных машинах производятся над конечными числами и с ограниченной точностью, определяемой разрядностью представления дискретных чисел. Цифровая информация, как правило, представляется при помощи электрических процессов, для которых характерны два состояния (например, включено/выключено, высокий/низкий уровень сигнала, ток есть/тока нет). Каждое такое состояние указывает на равенство значения двоичной переменной нулю или единице.

Арифметика, применяемая в компьютерах, отличается от арифметики, которая используется людьми:

· компьютеры выполняют операции над числами, точность которых конечна и фиксирована;

· в большинстве компьютеров используется не десятичная, а двоичная система счисления.

Когда люди выполняют какие-либо арифметические действия, их не волнует вопрос, сколько десятичных разрядов занимает то или иное число. Физики, к примеру, могут вычислить, что во Вселенной присутствует 10⁷⁸ электронов, и их не волнует тот факт, что полная запись этого числа потребует 79 десятичных разрядов. Никогда не возникает проблемы нехватки бумаги для записи числа.

С компьютерами дело обстоит иначе. В большинстве компьютеров количество доступной памяти для хранения чисел фиксировано и зависит от того, как и когда был разработан этот компьютер. Если приложить усилия, программист сможет представлять числа в два, три и более раз большие, чем позволяет размер памяти, но это не меняет природы данной проблемы. Память компьютера ограничена, поэтому мы можем иметь дело только с такими числами, которые можно представить в фиксированном количестве разрядов. Такие числа называются числами конечной точности.

Для примера, рассмотрим ряд положительных целых чисел, которые можно записать тремя десятичными разрядами без десятичной запятой и без знака. В этот ряд входит ровно 1000 чисел: 000,001, 002, 003,..., 999. При таком ограничении невозможно выразить определенные типы чисел:

1. Числа больше 999.

2. Отрицательные числа.

3. Дроби.

4. Иррациональные числа.

5. Комплексные числа.

Одно из свойств набора всех целых чисел — замкнутость по отношению к операциям сложения, вычитания и умножения. Другими словами, для каждой пары целых чисел i и j числа i+j, i-j и i×j — тоже целые числа. Ряд целых чисел не замкнут относительно деления, поскольку существуют такие значения i и j, для которых i/j не выражается в виде целого числа (например, 7/2 или 1/0).

Числа конечной точности не замкнуты относительно всех четырех операций. Рассмотрим операции над трехразрядными десятичными числами:

600+600=1200 (слишком большое число);

003-005=-2 (отрицательное число);

050×050=2500 (слишком большое число);

007/002=3,5 (не целое число).

Отклонения можно разделить на два класса:

операции, результат которых превышает самое большое число ряда (ошибка переполнения) или меньше, чем самое маленькое число ряда (ошибка из-за потери значимости),

операции, результат которых не является членом ряда.

Из четырех примеров, приведенных выше, первые три относятся к первому классу, а четвертый — ко второму классу.

Поскольку размер памяти компьютера ограничен, и он должен выполнять арифметические действия над числами конечной точности, результаты определенных вычислений будут неправильными с точки зрения классической математики. Вычислительное устройство, которое выдает неправильный ответ, может показаться странным на первый взгляд, но ошибка в данном случае — это только следствие его конечной природы. Некоторые компьютеры содержат специальное аппаратное обеспечение, которое обнаруживает ошибки переполнения и потери значимости.

Алгебра чисел конечной точности отличается от обычной алгебры. В качестве примера рассмотрим ассоциативный закон арифметики: a+(b-c)=(a+b)-c. Вычислим обе части выражения для а=700, b=400 и с=300. В левой части сначала вычислим значение (b-с). Оно равно 100. Затем прибавим это число к а и получим 800.

Чтобы вычислить правую часть, сначала вычислим (a+b). Для трехразрядных целых чисел получится переполнение. Результат будет зависеть от компьютера, но он не будет равен 1100. Вычитание 300 из какого-то числа, отличного от 1100, не даст результата 800. Ассоциативный закон не имеет силы. Таким образом, приходим к выводу, что важен порядок записи арифметической операций.

Аналогично можно рассмотреть другой закон — дистрибутивный:
а×(b-c)=a×b-a×c, для а=5, b=210 и с=195. В левой части 5×1×5=75. В правой части 75 не получится, поскольку a×b выходит за пределы ряда.

Исходя из этих примеров, можно было бы сделать вывод, что компьютеры совершенно непригодны для выполнения арифметических действий. Вывод естествен, но неверен. Эти примеры наглядно иллюстрируют важность понимания, как работает компьютер, и какие ограничения он имеет.

С точки зрения обычной арифметики, например, в интервале (–1; 1) имеется бесконечное множество "плотно" расположенных точек, причем в любой окрестности каждой такой точки имеется хотя бы одна точка из этого множества. Такую арифметику называют часто регулярной арифметикой. Машинная же арифметика имеет следующие особенности. Она нерегулярна – точки интервала сгущаются около нуля; кроме того, в этом интервале точка х "изолирована" – если взять любую ее окрестность (х – а; х + а), где а – число, которое не превосходит машинного нуля (наименьшего представимого в машине числа), то в этом интервале нет других точек (отличных от х). Говоря языком теории вероятности, плотности распределения чисел в регулярной и нерегулярной арифметике – различны, как, впрочем, плотности распределения целых и вещественных чисел в одной и той же арифметике. Множество вещественных чисел в машинной арифметике представляется как подмножество (определяемое разрядностью арифметики) множества рациональных чисел. Есть и другие особенности этих множеств (связанные, например, с выполнением операций), но указанные выше особенности – основные.

Различия в представлении чисел в обычной и в машинной (n-разрядной) арифметике ограничивают как "математические" возможности компьютера, так и "компьютерные" возможности математики, использование математических методов, алгоритмов в компьютерах.

Нужно всегда иметь в виду, что точность в теоретической математике – понятие абстрактное и в практической математике может возникать иллюзия точности там, где ее на самом деле нет, – если нет корректной договоренности о пределах возможных значений неизбежных погрешностей в рамках рассматриваемых вычислительных ресурсов, например, трудоемкости и времени, а также не оговорена стратегия управления этой погрешностью.

Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах 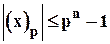, то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.

В 1937 году Конрадом Цузе для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также для повышения точности этого представления чисел было предложено представление чисел в плавающей, нормализованной форме – число x представляется в виде: , где m – мантисса числа, k – целый порядок числа,

Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k – под порядок, один разряд – под знак числа и один разряд – под знак порядка (например, 0 – плюс, 1 – минус), то диапазон представимых в форме с плавающей запятой чисел резко увеличивается (m + k + 2 = n):

(многоточие соответствует k единицам).

Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не различаются между собой. Числа, большие верхней границы положительных чисел, полагаются равными положительной бесконечности (меньшие нижней границы отрицательных – отрицательной бесконечности). Сравнение двух разных по величине чисел в арифметике с ограниченной разрядностью может поэтому приводить к неверному результату, как и сравнение двух равных в таких системах чисел с точки зрения математической.

Такое представление очень удобно для хранения в ЭВМ, так как на самом деле необходимо хранить не само число, а его знак, мантиссу, порядок и знак порядка, и все операции с числами сводятся к операциям с этими объектами. Операции же с этими объектами просты: сравнение знаков, увеличение, уменьшение порядка, сложение мантисс, нормализация, то есть в конечном итоге сводятся к достаточно просто реализуемым операциям сдвига, выравнивания, сравнения разрядов.

К "неудобствам" этой формы представления чисел можно отнести возможность возникновения следующих "особо опасных" ситуаций:

при сложении чисел с плавающей запятой (а, в конечном счете, все операции выполняются через сложение) происходит выравнивание порядков для последующего сложения мантисс, а при выравнивании степеней может происходить потеря (усечение) младших разрядов, например, такая ситуация может возникнуть при сложении одного "очень большого числа" с одним "очень малым числом"

при умножении чисел возможно образование порядка числа, превосходящего максимально возможный – переполнение.

Контрольные вопросы и задания

1.. Раскройте содержание понятия «информация».

2. Перечислите формы и виды информации.

3. Каковы важнейшие свойства информации?

4. Что такое система счисления?

5. В чем состоит главное отличие позиционных от непозиционных систем счисления?

6. Какие преимущества дает двоичная система счисления при представлении чисел в ЭВМ?

7. Что означает понятие «двоичное кодирование»?

8. Что такое бит и байт?

9. Перечислите наиболее распространенные единицы измерения информации. В каких случаях они используются?

Дата добавления: 2014-01-06