Двоично-десятичная система счисления

Уступка права требования по договору о совместной деятельности без согласия всех участников невозможна, поскольку это противоречит статье 388 Гражданского кодекса Российской Федерации.

Доля в общем имуществе, созданном в результате совместной деятельности, может быть определена пропорционально размеру фактических вкладов участников договора о совместной деятельности, если иное не предусмотрено условиями договора.

3. Учреждения и некоммерческие организации не могут быть участниками договора о совместной деятельности, только в случае когда такой договор заключен для осуществления предпринимательской деятельности.

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Двоично-десятичная система используется в цифровых автоматах, когда основная часть операция связана не с обработкой и хранением информации, а с её вводом и выводом на какие-либо индикаторы с 10ым представлением полученных результатов (калькуляторы, кассовые аппараты и т.п.).

В 2-10ой системе десятичные цифры от 0 до 9 представляются четырехразрядными двоичными комбинациями, т.е. двоичным эквивалентом десяти первых шестнадцатеричных цифр. Преобразования из 2-10ой системы и обратно не вызывает затруднений и выполняется путем прямой замены четырех двоичных цифр.

Две 2-10ые цифры составляют один байт, таким образом, с помощью одного байта в 2-10ой системе можно представить числа от 0 до 99, а не от 0 до 255 как при использовании 8ми разрядного двоичного числа. Используя один байт для представления каждых двух десятичных цифр можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов.

Например:

1001 0101 0011 1000 рассматривать как двоичное, то его десятичный эквивалент будет 38200, что в несколько раз больше 10-ичного эквивалента 2-10го числа (9538). Сложение 2-10ых чисел, имеющих один десятичный разряд выполняется так же, как и сложение четырехразрядных двоичных чисел без знака, за исключением того случая, когда результат превышает величину 1001, в этом случае необходимо производить коррекцию, которая осуществляется прибавлением к полученному результату числа 6 в 2ой системе (0110).

Если первоначальное двоичное сложение или прибавление корректирующего числа приводит к возникновению переноса, то при сложении многоразрядных 2-10ых чисел перенос осуществляется в следующий десятичный разряд.

Пример:

+6376

=8265

0001 1000 1000 1001

+0110 0011 0111 0110

=0111 1011 1111 1111

+0000 0110 0110 0110

=1000 0010 0110 0101

Представление числовой информации в ЭВМ

Информация в памяти ЭВМ записывается в виде цифрового двоичного кода. Для этого в ней имеются ячейки памяти и регистры для хранения двоичной информации. Большинство ячеек имеют одинаковую длину n для хранения n бит двоичной информации.

Бит – один двоичный разряд. Информация, хранящаяся в такой ячейке, называется словом, состоящим из одного байта информации.

На рисунке представлено двоичное слово, состоящее из двух байт. Ячейки памяти и регистры состоят из элементов памяти. Каждый из таких элементов может находиться в одном из двух устойчивых состояний. Например: конденсатор заряжен или разряжен, транзистор открыт или закрыт, высокое или низко сопротивление элемента, элемент намагничен или размагничен. Один из таких физических состояний создает высокий уровень выходного сигнала, а второе – низкий. Первое принимается, например, за единицу, а второе за 0 или наоборот. Память ЭАМ состоит из конечной последовательности слов, а они из конечной последовательности бит. Таким образом, так как объем представляемой в машине информацией ограничен её памятью, то числовая информация представляется с определенной точностью, зависящей от архитектуры памяти ЭВМ. В ЭВМ применяются две формы представления двоичных чисел. Первая – естественная или форма с фиксированной запятой или точкой. Вторая – нормальная или форма с плавающей точкой.

В форме с фиксированной точной все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением точки (или запятой), отделяющую целую часть от дробной. В этом случае разрядная сетка выглядит следующим образом:

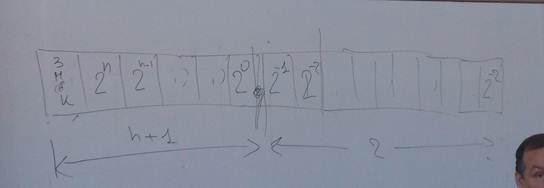
Если в результате какой-то операции получится число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки. Естественная форма представления чисел используется как вспомогательная и только для целых чисел, с плавающей точной каждое число изображается в виде двух групп цифр. Первое называется мантиссой, а вторая – порядком. При чем абсолютная величина мантиссы должна быть меньше единицы, а порядок – целым числом. В общем случае число с плавающей точкой или запятой может быть представлено в виде:

N=+-M*p^+-S, где M- мантисса, p - основание системы счисления, S – порядок числа.

M<1, |S|>0

Выполнение арифметических операций над целыми числами

В ЭВМ целые числа могут представляться без знака и со знаком. Целые числа без знака обычно занимают в памяти машины 1 или 2 байта (1 байт 0-255, 2 байта 0-65635).

Целые числа со знаком. Прямой, обратный и дополнительный коды.

Такие числа обычно занимают в памяти машины 1, 2 или 4 байта.

Прямой код.

Прямой, n-разрядный двоичный код отличается от двоичного тем, что в нем отводится один, как правило, самый старший разряд, для знака. А оставшиеся n-1 разряды для записи значащих цифр. Если знаковый разряд равен 0, то число положительное. Если 1, то отрицательное.

Для прямого кода справедливы следующие выражения:

n – разрядность кода, а_зн- значение знакового разряда.

Дополнительный код.

Использование чисел со знаком, т.е. прямого кода представления чисел усложняет структуру ЭВМ, в этом случае операция сложения двух чисел с разными знаками должна быть заменена операцией вычитания меньшего из большего и присвоению результату знака большей величины. Поэтому в современных машинах, как правило, отрицательные числа представляют в виде дополнительного или обратного кода, что при суммировании двух чисел с разными знаками позволяет заменить вычитание на обычное сложение, чем существенно упростить арифметико-логическое устройство ЭВМ. Смысл перевода отрицательных чисел из прямого в дополнительный и обратный коды рассмотрим на примере десятичных чисел.

Пусть ЭВМ оперирует с двухразрядными десятичными числами и необходимо сложить 2 числа.

X₁=84 и x₂=-32

Заменим код отрицательного слагаемого на его дополнение до ста и затем сложим x1 и x_доп

X_доп=100-32=68

Учитывая, что ЭВМ работает с двумя разрядами, третий разряд уходит.

X₁+X_доп=1(52)

Равенство полученного результата истинному значению объясняется тем, что при формировании дополнительного кода к x2 мы прибавляем сотню, а затем её вычитаем, отбрасыванием старшего разряда.

Операция вычитания ста заключается в том, что не учитывается код третьего десятичного разряда. Таким образом дополнение М, n-разрядного числа k будет величина M=pⁿ-k, где p – основание системы счисления.

Дополнительный код

Дополнение числа можно получить и без вычитания, перепишем выражение M вот таким образом: M=pⁿ-1=[(pⁿ-1)-k]+1 здесь число pⁿ-1 состоит из n цифр (p-1), т.е. старших цифр используемой системы счисления. Например для 10ой -> 9999; 16ой – FFFF

Поэтому величину в квадратных скобкам можно получить путем образования дополнений до (p-1) для каждой из цифр числа k в отдельности, а искомое дополнение суммированием этой величины с единицей. Так как в двоичной системе дополнение цифр до единицы соответствует их инверсным значениям, получается простое правило для получения дополнения для двоичных чисел:

1. Получить инверсию заданного числа

2. Образовать дополнительный код заданного числа путем прибавления единицы к инверсии этого числа.

Проверка правильности результата: сумма исходного числа и его дополнительного кода должна быть равна нулю (перенос единицы из старшего разряда не учитывается).

Старший вид дополнительного кода двоичных чисел выполняет функцию знака числа: 0 – положительное, 1 – отрицательное. При этом положительный числа в дополнительном коде изображаются так же как и в прямом: двоичными кодами с цифрой 0 в знаковом разряде. Для дополнительного кода справедливо следующее соотношение:

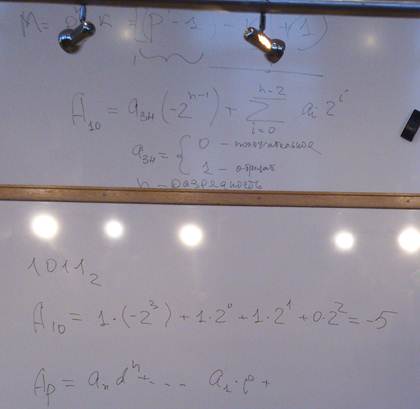
Пример: десятичная запись отрицательного числа, записанного в двоичном коде будет выглядеть:

Обратный код:

Для представления отрицательных чисел используется так же обратный код, который получается инвертированием всех цифр двоичного кода абсолютной величины числа, при этом необходимо помнить, что все операции с отрицательными числами выполняются в формате машинного слова, это значит, что двоичному числу слева дописываются нули, до нужного количества разрядов. Например для восьмиразрядного машинного слова с числом -1

Код модуля: 0000 0001

Обратный код: 1111 1110

Для -127

Код модуля: 0111 1111

Обратный код: 1000 0000

Для обратного кода справедливо следующее соотношение:

(фотка)

Для положительных чисел a_зн=0 и представление числа полностью совпадает с прямым и дополнительным кодом. Таким образом, положительные числа в прямом, обратном и дополнительном кодах отображаются одинаково: двоичным кодом с цифрой 0 в знаковом разряде. Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный код и в таком виде хранятся, перемещаются и участвуют в различных операциях. При выводе таких чисел происходит обратное преобразование в отрицательные десятичные числа.

Выполнение арифметических операций

Сложение и вычитание

Сложение обратных кодов.

При сложении двух чисел x и y имеет место 4 основных и 2 особых случая.

1. x и y>0 при суммировании складываются все разряды, включая разряд знака, так как у положительных чисел разряд равен 0, то и разряд суммы равен 0.

2. x>0, y<0 |y|>|x|

3+(-10)=-7 получим обратный код числа -10, тогда

1 111 0101

0 000 0011=

1 111 1000 – обратный код числа -7

Получили корректный результат в обратном коде, при переводе в прямой код, биты цифровой части результата инвертируются.

3. x>0, y<0 |y|<|x|

-3+ 10=7

0 000 1010+

1 111 1100= обратный код числа -3

0 000 0110+

1=

0 000 0111 (7)

Машина исправляет полученный первоначально некорректный результат 6 вместо 7, переносом единицы из знакового разряда в младший разряд суммы.

4. x<0 y<0

-3+(-7)=-10

1 111 1100+

1 111 1000=

1 111 0100+

1=

1 111 0101

Полученный первоначально некорректный результат обратный код числа -11 вместо обратного кода числа -10 машина исправляет переносом единицы из знакового разряда в младший разряд суммы. При переводе результата в прямой код биты цифровой части числа инвертируются, в результате получаем -10.

При сложении могут возникнуть ситуации, когда старшие разряды результата операции не помещаются в отведенную для него область памяти (переполнение разрядной сетки) для обнаружения переполнения и индикации ошибки в машине используются специальные средства.

1. (x+y)>0 x+y>=2ⁿ⁼¹ для однобайтового формата н=8

+47=

0 100 0001+

0 110 0001=

В ответе последняя единица – переполнение, так как 7ми разрядов недостаточно для размещения 8ми разрядной суммы. В результате происходит несовпадение знаков суммы и знаков слагаемых, что является свидетельством переполнения разрядной сетки.

2. x<0 y<0 |x|+|y|>=2^n-1

Для этого случая все аналогично, т.е. знак суммы не будет совпадать со знаками слагаемых

Сложение дополнительных кодов.

Здесь тоже имеют место рассмотренные выше 6 случаев.

Пример:

1. x>0 y>0 x+y<=2¹⁵

x=1594+

y=17563=

0 000 0110 0011 1010+

0 100 0100 1001 1011=

0 100 1010 1101 0101

Результат корректный

2. x>0 y<0 |x|<|y|

x=1594+

y=-17563=

-15969

0 000 0110 0011 1010+

1 011 1011 0110 0101=

1 100 0001 1001 1111

Результат корректен

3. x>0 y<0 |x|>|y|

y=-1594

x=17563

0 100 0100 1001 1011+

1 111 1001 1100 0110=

0 011 1110 0110 0001

Результат корректный

4. x<0 y<0 |x|+|y|<2¹³

x=-17503

y=-1594

-19157

1 011 1011 0110 0101+

1 111 1001 1100 0110=

1 011 0101 0011 1011

Результат корректен (перенос в старший разряд не учитывается)

5. x>0 y>0 |x|+|y|>2¹⁵

x=17563

y=19157

-28816

0 100 0100 1001 1011

0 100 1010 1101 0101=

1 000 1111 0111 0000

Корректный результат

При сложении двух положительных чисел получили отрицательный результат, так как произошло переполнение разрядной сетки.

6. x<0 y<0 |x|+|y|>2¹⁵

x=-17563

y=-19157

1 011 1011 0110 0101

1 011 0101 0010 1011=

0 111 0000 1001 0000

В 5ом и 6ом случае ограниченная разрядность чисел приводит к искажению не только величины, но и знака результата, добавляя к результату или вычитая из него (в случае 6) числа 2¹⁶. Для обеспечения корректности вычислений перед суммированием необходимо анализировать знаки слагаемых и результатов. Разные знаки слагаемых или совпадение знаков слагаемых со знаком суммы свидетельствует о том, что результат будет корректным. Для контроля за выполнением арифметических операций в процессоре машины содержится 2 индикатора: перенос и переполнение. Каждый индикатор содержит 1 бит информации и может иметь значение либо 1 либо 0. Индикатор переноса указывает на перенос из знакового бита, а индикатор переполнения на перенос в знаковый бит. В результате после завершения операции, в которой происходит перенос в старший бит, процессор устанавливает индикатор переполнения в единицу. Если переноса нет, то индикатор переполнения – обнуляется. Аналогично обрабатывается индикатор переноса. После выполнения операций машина сигнализирует о состоянии индикаторов и их можно проверить. Если состояние индикаторов указывает на неправильный арифметический результат, то необходимо принять меры, исправляющие данную ситуацию (пользователь может контролировать правильность выполнения арифметических операций).

Смещенный код.

Иногда его называют кодом с избытком. Он используется для упрощения операций над порядками чисел с плавающей запятой.

Формирование смещенного кода:

1. Выбирается длина разрядной сетки n

2. Последовательно записываются все возможные кодовые комбинации в обычной двоичной системе счисления

3. Кодовая комбинация с единицей в старшем разряде имеющая значение 2^n-1 выбирается для представления числа 0. Все последующие кодовые комбинации с 1ей в старшем разряде будут представлять числа +1, +2, +3 и т.д. А предыдущие -1, -2, -3 и т.д.

111 – +3

110 -+2

101 -+1

100 - 0

011 - -1

010 – -2

001 - -3

000 - -4

Например числа 3 и -3 со смещением для трехразрядной сетки будут иметь вид:

111 и 001, а для четырехразрядной сетки 1011 и 0101. Отсюда видно, что различия между двоичным кодом с избытком или смещенным кодом и двоичным дополнительным кодом состоит из противоположности значений знаковых битов, а разность значений кодовых комбинаций в обычном двоичном коде и двоичном коде с избытком равна для трехразрядной сетки 4ем, а для четырехразрядной сетки – 8ми.

В связи с этим смещенный код для трехразрядной сетки называют двоичным кодом с избытком 4, а для четырехразрядной – с избытком 8, для n-разрядной сетки он будет называться смещенным кодом с избытком 2^n-1. Смещенный код используется для упрощения операций над порядками чисел с плавающей запятой. Так при размещении порядка чисел 8ми разрядов используется двоичный код с избытком 128 и в этом случае порядок принимает значения от -128 до +127. Это позволяет работать с порядками, как с целыми числами без знака.

Код Грея.

Он широко используется в различных преобразовательных устройствах, в генетических алгоритмах и т.д. с тем чтобы разрешить проблемы связанные с возможностью одновременного изменения нескольких разрядов кодового слова. Характерной особенностью кода Грея является то, что в нем соседние кодовые слова различаются только в одном разряде.

Десятичный код Двоичный код Код Грея

0 0000 0000

1 0001 0001

2 0010 0011

3 0011 0010

4 0100 0110

Правила перевода числа из кода Грея в обычный двоичный код.

1. Первая единица со стороны старших разрядов остается без изменения.

2. Последующие цифры 0 и 1 остаются без изменения, если число единиц им предшествующих четно и инвертируется если не четно.

Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».

Пусть число 1011 записано в коде Грея. Получим запись этого числа в обычном двоичном коде.

1011 -> 1101

2ую слева инвертируем, так как количество единиц перед ней нечетно), третью цифру тоже инвертируем, так как перед ней только одна единица, четвертую оставляем без изменения, так как перед ней 2 единицы. Таким образом число записанное в коде грея

1011 записывается в двоичном коде как 1101.

Таким образом использование кода Грея позволяет свести погрешность к единице младшего разряда, например с измерительных устройств.

Представление вещественных чисел в ЭВМ.

Любое вещественное число N в системе счисления с основанием p можно представить в виде: N=+-M*p^+-S, где М - мантисса, а S – порядок и S – целое число. Такое представление числа называется представлением с плавающей запятой, где порядок определяет на сколько разрядов необходимо осуществить сдвиг относительно запятой. Очевидно, что если запятая в мантиссе стоит перед первой значащей цифрой, то при ограниченной разрядной сетке мы получаем максимальную точность представления числа. Отсюда следует, что мантисса должна быть правильной дробью |M|<1, у которой первая после запятой цифра a отлична от 0. |M|=0,a…. Для двоичной системы счисления a=1, следовательно мантисса будет выглядеть M=0,1… При выполнении этого требования число называется нормализованным. Нормализованная мантисса в двоичной системе счисления всегда представляется десятичным числом N в диапазоне 0,5<=n<1

Вещественные числа в машинах представляются, как правило, в трех форматах: одинарном, двойном и расширенном, имеющих одинаковую структуру

Здесь порядок n-разрядного нормализованного числа задается смещенным кодом, позволяющим производить операции над порядками, как над без знаковыми числами, что упрощает операции сравнения, сложения, вычитания порядков, а также операции сравнения самих нормализованных чисел.

Чем больше разрядов отводится под нормализованную мантиссу, тем выше точность. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего до наибольшего при заданном порядке.

В одинарном формате нормализованные числа в память записываются следующим образом: в 15ом бите первого машинного слова записывается знак числа, с 7го по 14ый бит записывается порядок, а мантисса занимает оставшиеся 23 бита в двух словах, несмотря на это в операциях участвуют 24 бита мантиссы, так как старший разряд мантиссы не хранится, он всегда равен 1, т.е. имеет место старший разряд, который при аппаратном выполнении операции автоматически восстанавливается и учитывается.

Порядок числа так же учитывает скрытый старший разряд мантиссы. Для двоичной точности используется 64ех разрядное нормализованное число со знаком, с 11ти разрядным смещенным порядком и 53ех разрядной мантиссой.

Расширенный формат – 80разрядное число со знаком, 15разрядный смещенный порядок и 64ехразрядная мантисса.

Примеры:

Дв.число: 0,000(1100)₂=0,(1100)₂*10^-3(10)

здесь порядок числа предоставляется с избытком 128

-3₁₀=(-3+128)₁₀=01111101₂

Здесь мантисса представлена бесконечной периодической дробью, потому последний учитываемый разряд мантиссы округляется.

Выполнение арифметических действий над нормализованными числами.

При алгебраическом сложении и вычитании числе представленных в формате с плавающей запятой, сначала выравниваются порядки слагаемых, при этом мантиссы числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов равное разности порядков операндов, после каждого сдвига порядок увеличивается на 1. В результате этого одноименные разряды чисел располагаются в соответствующих разрядов обоих регистров, после чего мантиссы складываются или вычитаются. При необходимости полученный результат нормализуется путем сдвига мантиссы результата влево и после каждого сдвига порядок результата уменьшается на 1.

Разность порядков равна 3, поэтому перед слоением мантисса первого числа сдвигается на 3 разряда вправо:

Дата добавления: 2014-01-06