
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Л 3. Сетевые модели
|
|
|
|
Сетевые модели и оптимизационные задачи на них тесно связаны с общей задачей линейного программирования. Они играют важную роль в оптимизационном планировании распределения продукции по складам, в оптимальном планировании перевозок и многих других применениях. Так, к примеру, сеть поставщиков может быть представлена в виде схемы (карты), которая в математике называется графом, состоящим из узлов (вершин) и дуг, соединяющих между собой некоторые пары узлов, называемых соседними. На рисунке узлы изображены точками, а дуги – линиями, соединяющими соответствующие точки. Принято различать ориентированные графы, дуги которых снабжены указанием направления в виде стрелок и неориентированными. Если дуги или узлы помечены некоторыми знаками, например, пропускными способностями, то подобный граф называется помеченным.
Пример1. У фирмы имеются три предприятия, выпускающих однотипную продукцию и четыре промежуточных склада, прикрепленных к предприятиям, согласно следующей схемы
Предприятия Склады


 1
1 
 1
1
 2
2

 2
2 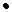
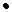 3
3
 3
3 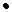
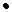 4
4
Эта схема представляет собой ориентированный граф с семью узлами (вершинами) и семью дугами.
дугами.
Классическая транспортная задача.
Рассмотрим частный случай, когда имеются производители 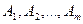 с ресурсами
с ресурсами 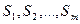 и потребители
и потребители 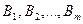 со спросами
со спросами 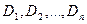 , соответственно. Если известны издержки сij доставки единицы ресурса от iго производителя к jому потребителю, то нетрудно построить классическую транспортную модель, вводя управляемые переменные
, соответственно. Если известны издержки сij доставки единицы ресурса от iго производителя к jому потребителю, то нетрудно построить классическую транспортную модель, вводя управляемые переменные  - допустимое количество товара, перемещаемое от iго поставщика jому потребителю. Переменные
- допустимое количество товара, перемещаемое от iго поставщика jому потребителю. Переменные 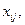
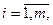
 удовлетворяют ограничениям
удовлетворяют ограничениям
 ,
, 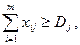
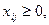
которые связаны с ресурсами производителей и спросом потребителей.
|
|
|
Изобразим транспортную модель в виде графа, собрав пометки в таблицу.
Производители Потребители
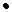 Ресурсы
Ресурсы 

 Спрос
Спрос
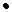
| Потребители Поставщики | В1 | В2 | … | Вn | Предложение |
| А1 | с11 х11 | с12 х12 | … | с1n х1n | S1 |
| А2 | с21 х21 | с22 х22 | … | с2n х2n | S2 |
| ... | … | … | … | … | … |
| Аm | сm хm1 | сm2 хm2 | … | сmn хmn | Sm |
| Спрос | D1 | D2 | … | Dn |
В таблице кроме издержек сij представлены: переменные хij, возможности Si поставщиков и спрос Dj – потребителей.
Теперь можно в рамках этой модели решать задачу оптимального по стоимости закрепления поставщиков за производителями
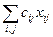
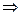


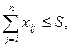

 ,
, 
Полученная задача является частным вариантом общей задачи линейного программирования. Здесь основной интерес представляет случай, когда суммарный спрос равен суммированному предложению
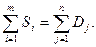
Это условие добавляет еще одно ограничение на область допустимых значений в пространстве 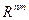 . В таком виде оптимизационная задача может быть решена либо общим симплекс-методом, либо специализированным методом потенциалов (см., например, [9]).
. В таком виде оптимизационная задача может быть решена либо общим симплекс-методом, либо специализированным методом потенциалов (см., например, [9]).
Задача о назначениях
Вариантом транспортной задачи является следующая задача о назначениях, когда имеется n работ, каждую из которых может выполнять один из исполнителей. Если известны стоимости сij исполнения iой работы jым исполнителем, то, используя транспортную модель, можно распределить исполнителей по работам, назначив одного исполнителя ровно на одну работу так, чтобы минимизировать общие затраты. Правда, теперь в рамках транспортной модели придется использовать т.н. булевы переменные
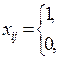 если iя работа исполняется jым работником
если iя работа исполняется jым работником
в остальных случаях. i,j=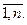
C участием этих переменных формируется оптимизационная задача

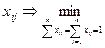

При небольших значениях величины n решение этой задачи можно получить простым перебором.
|
|
|
Пример 2. Пусть для 3х работ и 3х исполнителей матрица затрат имеет вид
С = 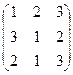
Здесь возможные назначения осуществляются одним из шести векторов (123), (132), (213), (231), (312), (321), координаты которых указывают на номер работы для 1го, 2го,3го исполнителя, соответственно. Вычисляя с помощью матрицы С значение функции в каждой из шести точек, обнаруживаем, что оптимальное назначение имеет вид (1,3,2), т.е. первый исполнитель назначается на первую работу, второй – на третью, а третий – на вторую. Минимальные суммарные затраты теперь равны 4.
В общем случае без использования специальных методов приходится перебирать 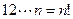 вариантов назначения.
вариантов назначения.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 310; Нарушение авторских прав?; Мы поможем в написании вашей работы!