Теорема Бернулли

Пусть производится 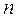независимых испытаний, в каждом из которых вероятность появления события 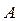равна 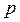. Можно ли предвидеть, какова примерно будет относительная частота появлений события? На этот вопрос дал положительный ответ Яков Бернулли (1713 год).

Теорема Бернулли. Если в каждом из 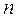независимых испытаний вероятность 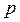появления события 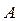постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 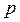по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если 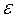- сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

.

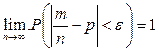Доказательство. Пусть 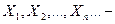числа появлений события в 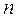испытаниях. Каждая из величин может принять лишь два значения: 1 (событие 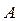наступило) с вероятностью 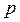и 0 (событие не появилось) с вероятностью .

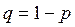Случайные величины 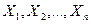попарно независимы, т.к. испытания независимы. Дисперсия любой величины 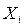, 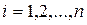равна произведению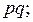 так как 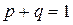, то произведение 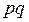не превышает 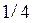и, следовательно, дисперсии всех случайных величин ограничены числом 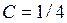, т.е.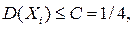 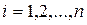. Следовательно, к случайным величинам 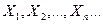можно применить теорему Чебышева (частный случай).

При этом будем иметь

.

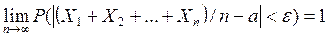Принимая во внимание, что математическое ожидание 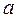каждой из величин 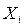(т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности 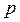наступления события, получим

.

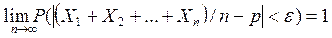Покажем, что дробь

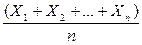равна относительной частоте 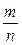появлений события 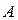в испытаниях. Каждая из величин 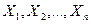при появлении события 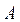в соответствующем испытании принимает значение, равное единице; следовательно, сумма 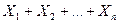равна числу 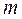появлений события в 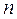испытаниях, значит

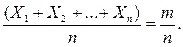
Учитывая это равенство, получим

.

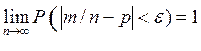Теорема Бернулли утверждает, что при относительная частота 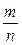при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности.

Коротко теорему Бернулли записывают так:

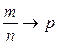при (закон больших чисел).

Глава 10. Функция распределения вероятностей случайной величины

Дата добавления: 2014-01-06