Коррелированность и зависимость случайных величин

Две слуайные величины и называют коррелированными, если их

корреляционный момент 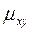или коэффициент корреляции 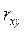отличен от нуля; и называют некоррелированными величинами, если их корреляционный момент или коэффициент корреляции равен нулю.

Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что а это противоречит условию, т.к. для коррелированных величин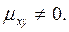

Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.

Пример. Двумерная случайная величина 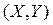задана плотностью распределения:

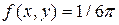внутри эллипса

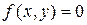вне этого эллипса.

Доказать, что и - зависимые некоррелированные величины.

Решение. Воспользуемся ранее вычисленными плотностями распределения составляющих и (п.12):

внутри заданного эллипса и

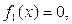
вне его.

Так как 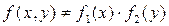, то и - зависимые величины (п. 16).

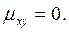Для доказательства некоррелированности и , достаточно, что Найдем корреляционный момент и по формуле

Функция 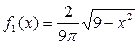симметрична относительно оси , следовательно, 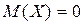; аналогично 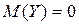, т.к. функция симметрична относительно оси .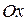

Следовательно,

(*)

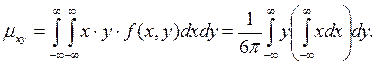Внутренний интеграл в (*) равен нулю, т.к. подынтегральная функция нечеткая, а пределы интегрирования симметричны относительно начала координат, следовательно, 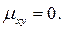То есть, зависимые случайные величины и некоррелированы.

Получили, из коррелированности двух случайных величин и , следует их зависимость, но из их зависимости еще не вытекает их коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще не следует независимость этих величин.

Заметим однако, что из некоррелированности нормально распределенных величин вытекает их независимость.

Дата добавления: 2014-01-06