Предел и непрерывность функции

Комплексное число b называется пределом функции f(z) при ,

.

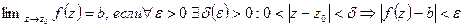Это определение – то же, что определение предела функции действительной переменной с той лишь разницей, что модуль здесь имеет смысл расстояния на комплексной плоскости, а не на действительной прямой, как раньше. Кроме того, окрестность точк и – не интервал с центром в этой точке, а круг без границы с центром в этой точке.

Функция называется непрерывной в точке , если .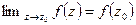

Функция называется непрерывной в области G, если она непрерывна в каждой точке этой области.

Область M называется областью однолистности функции , если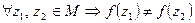

Линейная функция 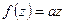осуществляет линейное отображение комплексной плоскости на себя. . Отсюда видно, что линейное отображение сводится к растяжению в 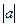раз и повороту на 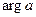комплексной плоскости. Здесь область однолистности – вся плоскость.

Инверсия 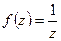() переводит все точки, лежащие вне единичной окружности внутрь и наоборот. Точки остаются на месте, единичная окружность отображается на себя.

Отображение () часть действительной оси () и верхнюю полуплоскость отображает на всю плоскость. Часть действительной оси () и нижняя полуплоскость тоже отображаются на всю плоскость. Здесь две области однолистности. Поэтому обратная функция двузначна.

Упражнение. Покажите, что при отображении существует n областей однолистности. Выделите их. Функция поэтому n – значна.

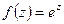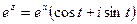Отображение переводит прямую, параллельную мнимой оси () в - окружность с центром в начале координат, радиусом . Прямая, параллельная действительной оси переводится в - луч из начала координат под углом y к действительной оси.

Поэтому полоса размером 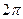вдоль действительной оси переводится во всю плоскость и представляет собой область однолистности (каждый отрезок в полосе, параллельный мнимой оси (x = a) отобразится в окружность радиуса a с центром в начале координат, меняя a, заполним этими окружностями всю плоскость). Следовательно, здесь бесконечное количество областей однолистности, а обратная функция - бесконечнозначна.

Производная функции комплексной переменной вводится так же, как и для функции действительной переменной

.

Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде

, то есть - бесконечно малая при . Главная линейная относительно часть приращения функции в точке , называется дифференциалом функции в точке , ( ).

Замечание. Функция двух переменных называется дифференцируемой в точке (), если ее приращение в этой точке можно представить в виде

++,

где , - бесконечно малые при ,

, .

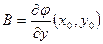Теорема. Для того, чтобыфункция была дифференцируема в точке , необходимо и достаточно, чтобы существовала ее конечная производная в этой точке.

Доказательство. Проводится так же, как и для функции действительной переменной с использованием теоремы о связи функции, предела и бесконечно малой.

Необходимость. Пусть функция дифференцируема в точке , тогда

,

Делим обе части на

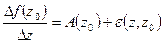. Так как - бесконечно малая при , то по теореме о связи функции, ее предела и бесконечно малой, .

Поэтому - формула для вычисления дифференциала.

Достаточность. Пусть в точке существует конечная производная функции . Тогда по теореме о связи функции, предела и бесконечно малой . Умножая на , получим . Следовательно, функция дифференцируема в точке .

Функция называется дифференцируемой в области, если она дифференцируема в каждой точке этой области.

Теорема (Коши – Римана). Для того, чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы ее действительная и мнимая части 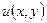, 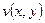были бы дифференцируемы в этой точке как функции двух переменных и в этой точке выполнялись бы условия Коши – Римана

, причем .

Замечание. С учетом условий Коши – Римана производная функции в точке может быть записана так: ==

==

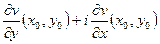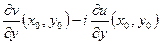
Необходимость. Пусть функция дифференцируема в точке z_0. Тогда

.

Пусть , .

.

Отделяя действительную и мнимую части, имеем:

,

.

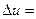
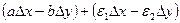Следовательно, функции дифференцируемы в точке

Из первого соотношения следует, что

.

Из второго соотношения следует, что

, .

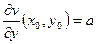Поэтому . .

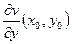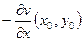Достаточность. Пусть функции дифференцируемы в точке и выполняются условия Коши – Римана.

где - бесконечно малые при .

.

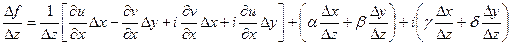Функции- бесконечно малые при , поэтому они являются бесконечно малыми при 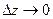. Справедливы неравенства . Поэтому отношения приращений в двух последних скобках – ограниченные величины. Следовательно, выражения в двух последних скобках – бесконечно малые величины при 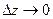как произведения бесконечно малых на ограниченные. Обозначим два последних слагаемых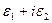 - бесконечно малая при .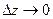

.

Умножая это выражение на , получим

.

Следовательно, функция дифференцируема в точке .

Условия Коши – Римана позволяют легко проверить дифференцируемость функции в точке.

Функция называется аналитической в области, если она дифференцируема в области.

Функция называется аналитической в точке, если она дифференцируема в этой точке и некоторой ее окрестности.

Дата добавления: 2014-01-06