Сводка теории. Общее представление об исчислении высказываний

Общее представление об исчислении высказываний

Таблицы истинности позволяют ответить на многие важные вопросы, касающиеся логических связок: является ли данная формула тавтологией, противоречием или ни тем и ни другим; влечет ли она логически другую данную формулу или являются ли две формулы логически равносильными.

Более сложные вопросы логики уже не могут быть решены с помощью истинностных таблиц или каких-либо других подобных эффективных процедур. Поэтому используется другой метод – аксиоматический.

При формализации математической теории полностью отвлекаются от ее содержания. Теоремы воспринимаются просто как формулы, которые могут быть выведены по определенным правилам. Поэтому формальные теории иначе называют исчислениями. О знаках и формулах исчисления приходится, однако, рассуждать содержательно: так, рядом с формальной теорией возникает «метатеория», которая тоже пользуется некоторыми обозначениями. Эти обозначения метатеории следует строго отличать от знаков и формул, относящихся к собственно формальной теории.

Существует много вариантов формализации логики высказываний. Опишем подробнее один из них; назовем его «теория L». Формальная (аксиоматическая) теория L считается определенной, если выполнены следующие условия:

1) Задано некоторое счетное множество символов теории L (языка теории). Основные символы теории L суть: пропозициональные буквы ,..., ,...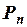; логические связки 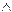, Ú, 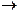, Ø; скобки (,).

Конечные последовательности символов теории называются выражениями теории L.

2) Имеется подмножество выражений теории L, называемых формулами теории и определяемых индуктивно с помощью следующих двух пунктов:

i) пропозициональные буквы суть формулы L;

ii) если A и B – формулы, то формулами являются и следующие выражения: , , , .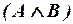

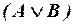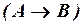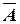3) Выделено некоторое множество формул, называемых аксиомами теории L, в рассматриваемом варианте теории их десять:

, (ив1)

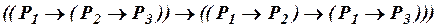, (ив2)

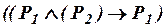, (ив3)

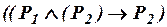, (ив4)

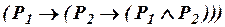, (ив5)

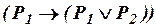, (ив6)

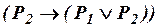, (ив7)

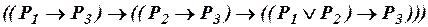, (ив8)

, (ив9)

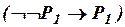(ив10)

Здесь 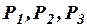– конкретные пропозициональные переменные, так что (ив1) – (ив10) есть список из десяти конкретных формул языка L.

4) Принимаются правила вывода, по которым можно из уже установленных теорем получать новые. В теории L – два таких правила вывода.

Первое правило имеет вид (MP) .

Это правило, называемое modus ponens (правило заключения ), утверждает, что если формулы 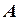и установлены как теоремы, то формула 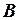также является теоремой.

Второе правило имеет вид: (S) .

Здесь суть формулы, – попарно различные пропозициональные буквы. Через 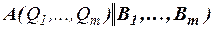обозначен результат одновременного замещения всех вхождений букв в 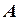на формулы соответственно. Отметим, что это правило подстановки (S) можно применять и к пропозициональным буквам 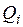, которые вовсе не входят в 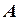. В этом случае соответствующее никуда не подставляется и просто не играет никакой роли.

Выводом назовем любую конечную последовательность формул 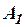, ,...,, такую, что каждая формула этой последовательности есть либо аксиома, либо совпадает с какой-либо предыдущей формулой этой последовательности, либо получается из каких-то предыдущих формул этой последовательности с помощью одного из правил вывода. Скажем, что вывод 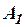,,...,является выводом своей последней формулы , и формулу назовем выводимой, или, что то же самое, теоремой теории. Будем записывать это в виде: L A или просто A.

В дальнейшем будем употреблять сокращенный вывод, когда в качестве могут стоять теоремы теории L, полученные раньше, имея в виду, что мы всегда можем дополнить вывод, вставляя недостающие его отрезки.

Дата добавления: 2014-01-06