
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовая последовательность и ее предел
|
|
|
|
О.1.Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Ограниченность.Функция, определенная на множестве называется ограниченной сверху (снизу) на этом множестве, если существует число, такое что для всех выполняется неравенство. Иначе функция называется неограниченной.
Число  и любое большее (меньшее) число называется верхней (нижней) гранью множества значений функции
и любое большее (меньшее) число называется верхней (нижней) гранью множества значений функции 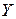 , а наименьшее (наибольшее) из чисел, ограничивающих множество
, а наименьшее (наибольшее) из чисел, ограничивающих множество 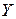 сверху (снизу), - точной верхней (нижней) гранью функции на множестве
сверху (снизу), - точной верхней (нижней) гранью функции на множестве  .
.
Например, функция 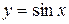 ограничена на всей числовой оси, так как
ограничена на всей числовой оси, так как 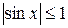 для любого
для любого  .
.
4. Периодичность. Функция 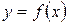 , определенная на множестве
, определенная на множестве 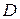 , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число 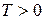 , что при любом
, что при любом 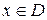 значение
значение  и
и 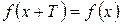 . При этом число
. При этом число  называется периодом функции.
называется периодом функции.
Если  - период функции, то ее периодами будут также числа
- период функции, то ее периодами будут также числа 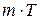 , где
, где 
За основной период берут наименьшее положительное число Т, удовлетворяющее равенству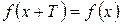 .
.
Если функции 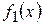 и
и 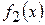 периодические с периодами
периодические с периодами 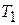 и
и  соответственно, то периодом их суммы, произведения, разности и частного является число
соответственно, то периодом их суммы, произведения, разности и частного является число  , кратное
, кратное 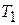 и
и  .
.
5. Явные и неявные функции. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция у=х2 +5х + 1.Функция 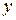 аргумента
аргумента  называется неявной, если она задана уравнением
называется неявной, если она задана уравнением  , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
, не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
 6. Обратная функция. Пусть
6. Обратная функция. Пусть 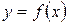 есть функция от независимой переменной
есть функция от независимой переменной  , определенной на множестве
, определенной на множестве  с областью значений
с областью значений 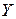 . Поставим в соответствие каждому
. Поставим в соответствие каждому  единственное значение
единственное значение  , при котором
, при котором  . Тогда полученная функция
. Тогда полученная функция 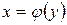 , определенная на множестве
, определенная на множестве 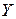 с областью значений
с областью значений  , называется обратной.
, называется обратной.
|
|
|
Обратную функцию обозначают так же в виде 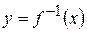 . Например, для функции у=ах обратной будет функция х=logaу или (в обычных обозначениях зависимой и независимой переменных) у= loga x.
. Например, для функции у=ах обратной будет функция х=logaу или (в обычных обозначениях зависимой и независимой переменных) у= loga x.
Таким образом, функция 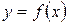 имеет обратную, тогда и только тогда, когда выполняется взаимно-однозначное соответствие между множествами
имеет обратную, тогда и только тогда, когда выполняется взаимно-однозначное соответствие между множествами  и
и  . Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
 Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
7. Сложная функция. Пусть функция 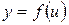 есть функция от переменной
есть функция от переменной 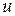 , определенной на множестве
, определенной на множестве 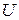 с областью значений
с областью значений 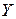 , а переменная
, а переменная 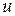 в свою очередь является функцией
в свою очередь является функцией 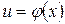 от переменной
от переменной  , определенной на множестве
, определенной на множестве  с областью значений
с областью значений 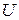 . Тогда заданная на множестве
. Тогда заданная на множестве  функция
функция  называется сложной функцией.
называется сложной функцией.
Переменную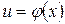 называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Например,  — сложная функция, так как ее можно представить в виде
— сложная функция, так как ее можно представить в виде 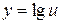 , где
, где 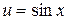 .
.
§2. Основные элементарные функции, классификация функций. Преобразование графиков функций
К основным элементарным относятся следующие функции: степенная функция у=хα, α 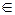 R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы.
R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы.
Например, функции  ;
;  является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции конечно.
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции конечно.
Примерами неэлементарных функций являются функции у= | х |, у= [ х ].
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
|
|
|
Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:
1) целая рациональная функция (многочлен или полином):
 ;
;
2) дробно-рациональная функция — отношение двух многочленов;
3) иррациональная функция (если в составе операций над аргументом имеется извлечение корня).
Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
Рассмотрим методику построения графиков функций, основанную на применении некоторых правил построения по уже известным графикам функций.
Правило 1. Чтобы получить график функции 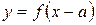 из графика функции
из графика функции 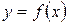 , нужно график функции
, нужно график функции 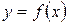 сдвинуть вдоль оси
сдвинуть вдоль оси 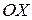 на
на 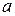 вправо, если
вправо, если  , или на
, или на  влево, если
влево, если  .
.
Правило 2. Чтобы получить график функции  из графика функции
из графика функции 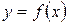 , нужно график функции
, нужно график функции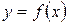 сдвинуть вдоль оси
сдвинуть вдоль оси 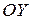 на
на 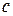 вверх, если
вверх, если  , или на
, или на  вниз, если
вниз, если  .
.
Правило 3. Чтобы получить график функции  из графика функции
из графика функции 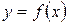 , нужно график функции
, нужно график функции 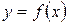 зеркально отразить относительно оси
зеркально отразить относительно оси 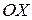 .
.
Правило 4. Чтобы получить график функции 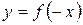 из графика функции
из графика функции 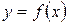 , нужно график функции
, нужно график функции 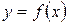 зеркально отразить относительно оси
зеркально отразить относительно оси 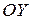 .
.
Правило 5. Чтобы построить график функции  , нужно значение ординаты графика функции
, нужно значение ординаты графика функции 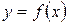 умножить на число
умножить на число 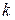 , а абсциссу оставить без изменения.
, а абсциссу оставить без изменения.
При этом от умножения всех значений функции 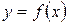 на
на 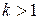 ординаты графика функции увеличатся в
ординаты графика функции увеличатся в 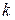 раз и происходит «растяжение» графика функции
раз и происходит «растяжение» графика функции 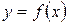 от оси
от оси 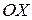 в
в 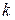 раз, а от умножения на
раз, а от умножения на 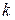 при
при  ординаты графика функции уменьшаются в
ординаты графика функции уменьшаются в 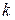 раз и происходит «сжатие» графика функции
раз и происходит «сжатие» графика функции 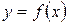 к оси
к оси 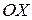 в
в 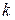 раз.
раз.
Правило 6. Чтобы построить график функции 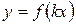 , нужно значение
, нужно значение  разделить на число
разделить на число 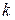 .
.
При этом от деления всех значений аргумента функции 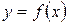 на
на 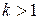 график функции «сжимается» к оси
график функции «сжимается» к оси 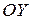 в 1∕к раз, а от деления на
в 1∕к раз, а от деления на 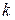 при
при  график функции «растягивается» от оси
график функции «растягивается» от оси 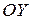 в 1∕к раз.
в 1∕к раз.
Правило 7. Чтобы получить график функции  из графика функции
из графика функции 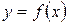 , надо участки графика функции
, надо участки графика функции 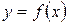 , лежащие выше оси
, лежащие выше оси 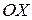 , оставить без изменения, а участки ниже оси
, оставить без изменения, а участки ниже оси 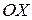 зеркально отразить относительно этой оси.
зеркально отразить относительно этой оси.
Правило 8. Чтобы получить график функции у= f(|х|) из графика функции 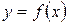 , надо построить график функции
, надо построить график функции 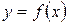 , при
, при  и отразить его зеркально относительно оси
и отразить его зеркально относительно оси  .
.
|
|
|
О. 1. Если по некоторому закону каждому натуральному числу  поставлено в соответствие вполне определенное число
поставлено в соответствие вполне определенное число 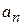 , то говорят, что задана числовая последовательность {
, то говорят, что задана числовая последовательность {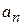 }:
}: 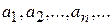 (
( ).
).
Другими словами, числовая последовательность — это функция натурального аргумента: 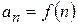 .
.
При этом числа ( ) называются членами последовательности, число
) называются членами последовательности, число 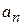 — общим или
— общим или  - м членом данной последовательности.
- м членом данной последовательности.
Примеры числовых последовательностей:
2, 4, 6, 8,..., 2 n,... (монотонная, неограниченная), (1)
1, 0, 1, 0,... (не монотонная, ограниченная), (2)
0; 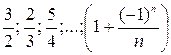 , … (не монотонная, ограниченная). (3)
, … (не монотонная, ограниченная). (3)
Чаще всего последовательность задается формулой ее общего члена, c помощью которой можно вычислить любой член последовательности. Так равенства: 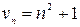 ;
; 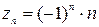 ;
; 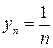 ;
; 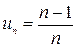 ;
;  .
.
Задают соответственно последовательности:
 (4)
(4)
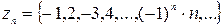 (5)
(5)
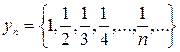 (6)
(6)
 (7)
(7)
О.2. Последовательность 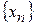 называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число 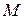 (число
(число  ) такое, что любой элемент
) такое, что любой элемент 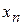 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству 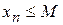 (
(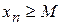 ).
).
О.3. Последовательность 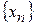 называется ограниченной, если она ограничена и сверху и снизу, т.е. если существуют числа
называется ограниченной, если она ограничена и сверху и снизу, т.е. если существуют числа 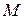 и
и  такие, что любой элемент
такие, что любой элемент 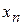 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству  .
.
О.4. Последовательность 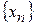 называется неограниченной, если для любого числа
называется неограниченной, если для любого числа  существует элемент
существует элемент 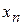 этой последовательности, удовлетворяющий неравенству
этой последовательности, удовлетворяющий неравенству 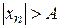 .
.
Легко видеть, что последовательности  и
и  – ограничены, а
– ограничены, а 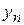 и
и 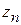 – неограниченны.
– неограниченны.
Рассмотрим числовую последовательность
0; 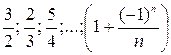 , …
, …
Изобразим ее члены точками числовой оси.

Можно заметить, что члены последовательности 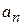 с ростом
с ростом  близко приближаются к 1. При этом абсолютная ветчина разности
близко приближаются к 1. При этом абсолютная ветчина разности  становится все меньше и меньше. Действительно:
становится все меньше и меньше. Действительно: 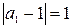 ,
,  ,
,  ,
, 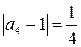 , …,
, …, 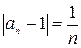 , …. т.е. с ростом
, …. т.е. с ростом  величина
величина  будет меньше любого очень маленького положительного числа.
будет меньше любого очень маленького положительного числа.
О.5. Число 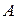 называется пределом числовой последовательности
называется пределом числовой последовательности 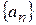 , если для любого числа
, если для любого числа 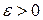 , существует такой номер
, существует такой номер 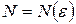 , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами 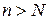 выполняется неравенство
выполняется неравенство 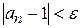 .
.
Пример. Показать, что предел 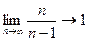
Решение: 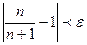
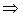

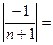

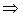
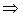

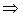
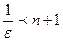
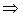

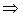
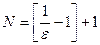
Число 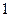 является пределом последовательности с общим членом
является пределом последовательности с общим членом 
 .
.
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 328; Нарушение авторских прав?; Мы поможем в написании вашей работы!