Напряжения на наклонных площадках

Покажем, что если известны компоненты напряженного состояния в точке на трех взаимно перпендикулярных площадках, то напряженное состояние тем самым полностью определено, т.е. могут быть найдены напряжения на любой другой площадке, проходящей через эту точку.

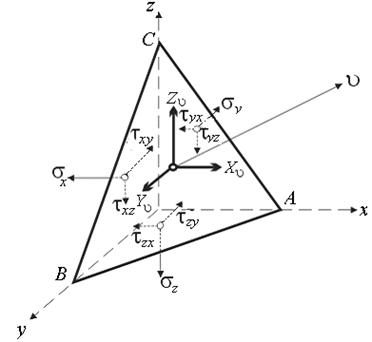
Рис.14.2

Выделим в окрестности рассматриваемой точки K элементарный тетраэдр, образованный тремя координатными площадками и произвольно наклоненной к ним площадкой ABC. Положение площадки в пространстве зададим направляющими косинусами ее нормали ν¯, обозначив:

cos (νˉ¸x) = l,

cos(νˉ¸y) = m,

cos(ν ˉ¸z) = n.

Считая размеры тетраэдра бесконечно малыми, напряжения на его гранях можно считать равными напряжениям в точке K, но действующим на площадках, по разному ориентированных в пространстве.

Напряжения на координатных площадках будем считать заданными; они изображены пунктиром, поскольку действуют на невидимых гранях элементарного четырехгранника. Полное напряжение p _ν на наклонной грани разложим на проекции по осям координат X_u, Υ_u, Ζ_u. Обозначив площадь наклонной грани dA, найдем площади остальных граней элемента проектированием величины dA на соответствующие координатные плоскости:

A_KBC = dA_x = dA·l;

A_КАС = dA_y = dA·m;

A_KAB = dA_z = dA·n.

Запишем условия равновесия выделенного элемента, приравняв нулю сумму проекций всех сил на оси координат:

ΣF_x = 0 X_ν · dA – σ _x ·dA·l ­ τ _yx·dA·m ­ τ _zx ·dA·n = 0.

Проектируя силы на две другие оси и сокращая на общий множитель dA, получаем выражения для напряжений на наклонной площадке:

X_ν = σ _x l + τ _yx m + τ _zxn¸

Y_ν = τ _xy l + σ _ym + τ _zy n,

Z_ν = τ _xzl + τ _yzm + σ _zn. (14.1)

Эти формулы позволяют найти напряжения на любой площадке с направляющими косинусами l, m, n по известным компонентам напряженного состояния на трех взаимно перпендикулярных площадках.

ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ

Полный вектор напряжений p _ν, действующий на наклонной площадке, можно разложить не только на координатные проекции Χ_u, Υ_u, Ζ_u, как мы поступили ранее, но так же на нормальную составляющую σ_u и касательную τ_u, действующую в плоскости грани.

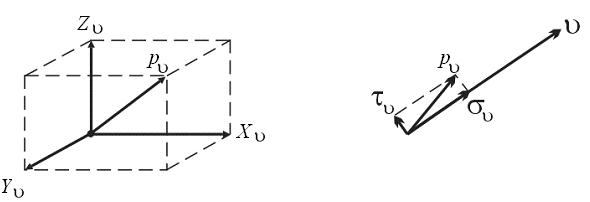
Рис. 14.3

При этом очевидны равенства:

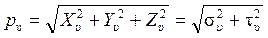
При изменении положения наклонной грани элемента меняется соотношение между σ _ν и τ _{ν .} Возможна ситуация, при которой касательная составляющая τ _ν обращается в нуль, т.е. полное напряжение p _ν совпадает по направлению с нормалью к площадке. Такие площадки, на которых нет касательного напряжения, называют главными площадками. Действующие на них напряжения обозначают σ и называют главными напряжениями. Поскольку главное напряжение является нормальным, его проекции на оси координат можно найти следующим образом:

Χ_ν = σ l; Υ_ν = σ m; Z_ν = σ n.

Подставляя эти выражения в (14.1), получим:

σ l = σ _xl + τ _yxm + τ _zxn,

σ m = τ _xyl + σ _y m + τ _zyn, (14.2)

σ n = τ _xzl + τ _yzm + σ _zn

или, перенося все в правую часть:

(σ _x - σ) l + τ _yxm + τ _zx n = 0,

τ _xy l + (σ _y - σ) m + τ _zyn = 0, (14.3)

τ _xz l + τ _yz m + (σ _z - σ) n = 0.

Полученные выражения (14.3) можно рассматривать, как однородную систему линейных алгебраических уравнений относительно неизвестных направляющих косинусов главных площадок. Чтобы такая система имела ненулевые решения, ее определитель должен быть равен нулю:

σ _x – σ τ _yx τ _zx

det τ _xy σ _y – σ τ _zx = 0.

τ _xz τ _yz σ _z – σ

Раскрыв определитель по обычным правилам, получим так называемое характеристическое уравнение, представляющее собой кубическое уравнение относительно неизвестных напряжений σ:

σ ³ - Ι₁ σ ² + I₂ σ - I₃ = 0 (14.4)

Здесь обозначено I ₁ = σ _x + σ _y + σ _z;

I ₂ = σ _y· σ _z + σ _z· σ _x + σ _x· σ _y – τ _yz² – τ _zx² – τ _xy²

σ _x τ _yx τ _zx

I ₃ = det τ _xy σ _y τ _zy (14.5)

τ _xz τ _yz σ _z

Уравнение (14.4) имеет три корня, которые называют главными напряжениями и обозначают в порядке алгебраического убывания σ₁, σ₂, σ₃. Поскольку главные напряжения не могут зависеть от выбранной системы координат, коэффициенты (14.5) характеристического уравнения постоянны и называются инвариантами напряженного состояния.

Каждому из главных напряжений соответствует своя главная площадка. Примем пока без доказательства тот факт, что главные площадки взаимно перпендикулярны друг другу. Для нахождения положения главных площадок, можно воспользоваться системой уравнений для направляющих косинусов (14.3), дополненной известным из тригонометрии условием:

l² + m² + n² = 1.

Подставляя поочередно вместо σ значения найденных главных напряжений σ₁, σ₂, σ₃, будем получать системы алгебраических уравнений для нахождения направляющих косинусов соответствующей главной площадки.

Если выбрать систему координат таким образом, чтобы оси совпадали с нормалями к главным площадкам, то напряженное состояние в точке можно изобразить так, как показано на рис.14.4.

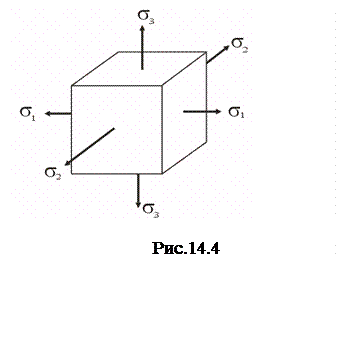
Такой вид напряженного состояния, при котором все главные напряжения отличны от нуля, называют объемным. Однако возможна ситуация, когда одно или два главных напряжения равны нулю. При изучении растяжения и сжатия мы встретились с напряженным состоянием, при котором от нуля отличалось лишь одно главное напряжение, действующее в поперечном сечении стержня. При растяжении оно было положительным, при сжатии – отрицательным. Учитывая правило нумерации главных напряжений, это можно представить графически следующим образом:

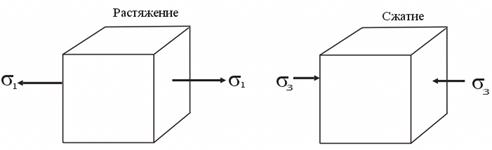
Рис.14.5

Такое напряженное состояние называют линейным или одноосным.

Случай, при котором от нуля отличны два главных напряжения, называют плоским напряженным состоянием (сокращенно ПНС), графически его можно представить так:

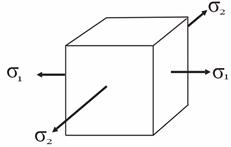
Рис. 14.6

В инженерных задачах плоское напряженное состояние встречается довольно часто, поэтому в следующей лекции рассмотрим его подробнее.

Дата добавления: 2014-01-06