
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Стратегическая эквивалентность кооперативных игр
|
|
|
|
Игра 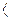 I, V
I, V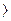 стратегически эквивалентна игре
стратегически эквивалентна игре 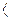 I, V’
I, V’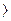 , (V~V’), если
, (V~V’), если 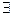 k>0, c
k>0, c , i
, i I: V’(K) = kV(K) +
I: V’(K) = kV(K) +  ,
,  k
k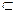 I.
I.
Стратегическая эквивалентность обладает следующими свойствами:
· Рефлексивность (V~V);
· Симметрия (V~V’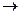 V’~V);
V’~V);
· Транзитивность (V~V’, V’~V’’ 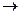 V~V’’).
V~V’’).
Т. о. стратегическая эквивалентность является отношением, которое разбивает множество кооперативных игр на непересекающиеся классы, т. к. если V~V’, то дележу x = (x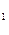 , x
, x ,…,x
,…,x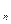 ) соответствует делёж x’ = (x’
) соответствует делёж x’ = (x’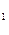 , x’
, x’ ,…,x’
,…,x’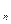 ), где x’
), где x’ = kx
= kx + c
+ c , i =
, i = 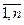 .
.
Если V(K) = 0,  k
k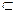 I, то игра
I, то игра 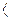 I, V
I, V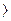 называется нулевой. Любая несущественная коалиционная игра эквивалентна нулевой игре.
называется нулевой. Любая несущественная коалиционная игра эквивалентна нулевой игре.
В 0,1-редуцированной форме дележом может быть любой вектор x = (x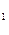 , x
, x ,…,x
,…,x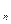 ), компоненты которого удовлетворяют условиям: а) x
), компоненты которого удовлетворяют условиям: а) x
 0;
0;
б) 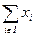 = 1.
= 1.
Каждой характеристической функции V(k) можно сопоставить множество дележей, удовлетворяющих условиям:
1. x
 V(i);
V(i);
2. x(I) = V(I);
3. x
 0,
0, 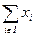 = 1.
= 1.
При решении корпоративной игры необходимо найти единственно справедливый делёж. Для решения используется несколько предположений:
Введём отношение предпочтения дележей x >x
>x (при коалиции k)
(при коалиции k)
x
 x
x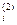 , i
, i I
I x
x (I) = V(I)
(I) = V(I)
Если для коалиции, то x (k)
(k) 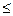 V(k), k
V(k), k I. Это условие практической реализуемости дележа.
I. Это условие практической реализуемости дележа.
Отношение дележей возможно не по всем коалициям.
1. k = 1 — коалиция из одного игрока
x
 y
y , x
, x
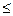 V(i) — это условие противоречит условию индивидуальной рациональности.
V(i) — это условие противоречит условию индивидуальной рациональности.
2. k = I — коалиция из всех игроков
x(I) > y(I) = V(I)
Таким образом, отношение доминирования можно изучать для классов стратегической эквивалентности. Причём, в качестве таких классов можно рассматривать либо несущественные игры, либо игры в 0,1-редуцированной форме. Отношение предпочтения и другие свойства позволяют определить некоторое множество дележей. Теория кооперативных игр занимается изучением множества дележей, удовлетворяющим рассмотренным свойствам.
|
|
|
Доминирование дележей невозможно по следующим коалициям:
· из одного игрока, т. к. если y < x
< x
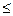 V(i), противоречит условию индивидуальной рациональности.
V(i), противоречит условию индивидуальной рациональности.
· из всех игроков, т. к. 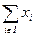 >
> = V(I) противоречит условию коллективной рациональности.
= V(I) противоречит условию коллективной рациональности.
Пусть есть две стратегически эквивалентных игры V~V’ и некоторые два дележа  и
и  , которые будут доминировать, соответственно, дележам:
, которые будут доминировать, соответственно, дележам:  >
>  ,
, 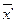 >
> 
Можно показать, что если выполняется первое неравенство, то будет выполняться и второе по этой коалиции 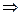 отношения доминирования могут исследоваться на примере наиболее простых игр каждого класса.
отношения доминирования могут исследоваться на примере наиболее простых игр каждого класса.
Для несущественных игр отношение доминирования можно рассматривать на примере нулевой игры, а для существенных на примере 0,1-редуцированной игры.
Рассмотрим доминирование дележей существенной игры трёх лиц:
x = (x , x
, x , x
, x ) – вектор дележей, x
) – вектор дележей, x
 V(i), x
V(i), x + x
+ x + x
+ x = 1
= 1

Этот барицентрический треугольник называется двумерным симплексом.
Например, в симплексе зафиксировано x = x
= x (прямая, параллельная АВ, будет иметь положение в зависимости от V
(прямая, параллельная АВ, будет иметь положение в зависимости от V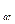 ).
).
Подмножество С множества допустимых значений, где выполняются условия:
1) нет доминируемых дележей по любой коалиции из I;
2) для любой коалиции k I выполняются условие x(k)
I выполняются условие x(k)  V(k),
V(k),  k
k I, называют С-ядром кооперативной игры с характеристической функцией V(k).
I, называют С-ядром кооперативной игры с характеристической функцией V(k).
Компоненты С-ядра должны удовлетворять некоторой конечной системе линейных неравенств.
Рассмотрим методику составления неравенств на примере игры трёх лиц.
Эти неравенства: V(1,2)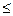 x
x +x
+x
V(1,3)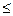 x
x +x
+x
V(2,3)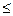 x
x +x
+x
К этим неравенствам добавляются ещё два неравенства индивидуальной групповой рациональности x
 V(1), x
V(1), x
 V(2), x
V(2), x
 V(3), x
V(3), x + x
+ x + x
+ x = 1
= 1
При приведении этой игры к 0,1-редуцированной форме, получаем:
V(1) = V(2) = V(3) = 0
x
 0, I = 1,2,3
0, I = 1,2,3
x + x
+ x
 c
c
x + x
+ x
 c
c
x + x
+ x
 c
c , c
, c
 0
0
Условие нахождения С-ядра рассмотрим на следующем примере:
Пусть есть три предприятия П , П
, П , П
, П .
.
|
|
|
П – Д
– Д , Д
, Д по 900 шт.
по 900 шт.
П – Д
– Д , Д
, Д по 700 шт.
по 700 шт.
П – М
– М , М
, М по 1000 шт.
по 1000 шт.
Поступил заказ поставить комплект товаров (Д , М
, М ) по 1000 шт. Каким образом скомплектовать этот заказ?
) по 1000 шт. Каким образом скомплектовать этот заказ?
Другими словами, как распределить величину Д относительно П
относительно П и П
и П ?
?
Данный конфликт можно моделировать кооперативной игрой трёх лиц, где участники могут заключать между собой соглашения и компенсировать друг другу их значимость.
Будем считать характеристическую функцию в единицах товаров.
V(П ) = V(П
) = V(П ) = V(П
) = V(П ) = V(П
) = V(П , П
, П )
)
V(П , П
, П ) = 1800
) = 1800
V(П , П
, П ) = 1400
) = 1400
V(П , П
, П , П
, П ) = 2000
) = 2000
Перейдём к 0,1-редуцированной форме, тогда V(П ) = V(П
) = V(П ) = V(П
) = V(П )=0 V(П
)=0 V(П , П
, П ) = 0
) = 0
V(П , П
, П ) = 0,9
) = 0,9
V(П , П
, П ) = 0,7
) = 0,7
V(П , П
, П , П
, П ) = 1
) = 1
Для дележей получим следующие неравенства:
 . Это условие определяет С-ядро этой игры.
. Это условие определяет С-ядро этой игры.
 Последнее неравенство определяет двумерный симплекс. Рассмотрим прямую x
Последнее неравенство определяет двумерный симплекс. Рассмотрим прямую x + x
+ x = 0,9. Это эквивалентно множеству точек, когда x
= 0,9. Это эквивалентно множеству точек, когда x = 0,1; x
= 0,1; x + x
+ x = 0,7;
= 0,7;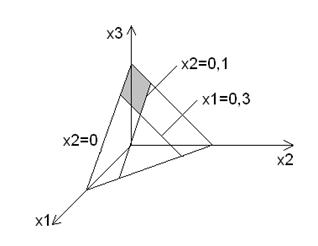 x
x = 0,3
= 0,3
— множество дележей, образует С-ядро этой игры. Любой делёж из этого ядра является наилучшим.
Например, x = 600 ед.
= 600 ед.
x = 200 ед.
= 200 ед.
x = 1200 ед.
= 1200 ед.
Превышение x над x
над x и x
и x за счёт монополии; П
за счёт монополии; П и П
и П придется доплачивать П
придется доплачивать П , т. к. они не могут самостоятельно выполнить заказ.
, т. к. они не могут самостоятельно выполнить заказ.
Д =
= 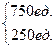 ,
,
М = 1000 ед.
= 1000 ед.
П доплатит 150 ед., а П
доплатит 150 ед., а П – 50 ед.
– 50 ед.
Более общим подходом к решению кооперативных игр является решение по Нейману-Моргенштерну. Н-М решения, как и с-ядро, определяют множество эквивалентных между собой решений.
Кроме С-ядра и Н-М решения для определения предпочтительного дележа используют вектор Шепли.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 650; Нарушение авторских прав?; Мы поможем в написании вашей работы!