
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы
|
|
|
|
Состояние частицы в неинерциальной системе 
| Название и математическое выражение силы инерции | Характер движения  относительно ИСО относительно ИСО 
|
| Частица находится в покое | Сила инерции

| Система  движется прямолинейно с ускорением движется прямолинейно с ускорением 
|
Центробежная сила инерции

| Система  вращается с угловой скоростью вращается с угловой скоростью 
| |
Частица движется со скоростью 
| Кориолисова сила инерции
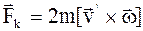
|
Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений (подмывание берегов рек; неравномерное изнашивание железнодорожных рельсов; отклонение падающих на поверхность Земли тел; поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли). Применительно к рассмотренному выше случаю движения можно привести такой пример: при стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в направлении на запад (т.е. в направлении, противоположном вращению Земли), и поднимать кверху, если выстрел произведен в восточном направлении.
Таким образом, основной закон динамики для неинерциальных систем отсчета можно записать в виде
m a ’= F + F ин+ F ц+ F к, (3.37)
где F, F ин, F ц, F к - ранее рассмотренные силы, действующие в неинерциальных системах отсчета.
Надо еще раз отметить, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Два основных положения динамики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются.
|
|
|
Для любого из тел, находящегося в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, момента импульса, энергии.
Силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил нет.
Силы инерции пропорциональны массам частиц (тел, систем) и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в "поле сил инерции" эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящиеся под действием сил поля тяготения.
При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном, висящем в однородном поле тяготения. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.
Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна): «Все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы». Этот принцип является основой общей теории относительности.
3.4. Элементы динамики материальной точки и твердого тела, совершающих вращательное движение относительно неподвижной оси вращения. Основные понятия и определения: момент силы, момент импульса, момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения
|
|
|
Основной задачей динамики вращательного движения является задача нахождения угловых ускорений, сообщаемых известными силами. Однако одна и та же сила, в зависимости от расстояния между ее направлением и осью вращения, сообщает различные угловые ускорения. Для описания вращательного движения введены специфические параметры: момент силы, момент инерции тела, момент импульса. Благодаря этим параметрам достигается подобие основных уравнений динамики поступательного и вращательного движения.
Момент силы характеризует вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и оси вращения.
Моментом силы относительно центра вращения называют векторную физическую величину, модуль которой равен произведению модуля силы на плечо:
ç M ç= ç F ç×l или M = F×l, (3.38)
где l - плечо силы - кратчайшее расстояние от направления действия силы до центра вращения.
Вектор M направлен вдоль перпендикуляра к плоскости, на которой находится центр вращения и сила. Направление его определяется правилом правого винта. Так как
l = r×sinα,
гдеr численное значение радиус-вектора r, который направлен из центра вращения в точку приложения силы;
α - угол между направлениями F и r,
то
M = F×r×sinα (3.39)
или в векторной форме
M = [ r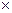 F ]. (3.40)
F ]. (3.40)
Момент нескольких сил, имеющих одну точку приложения, равен алгебраической сумме моментов слагаемых сил:
 . (3.41)
. (3.41)
Этот момент называют главным или результирующим моментом системы сил относительно неподвижной точки вращения (центра; полюса).
Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему. Иначе результирующий момент внутренних сил системы равен нулю.

|
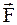 ,
, 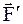 .
.  ,
,  – радиус-вектора, проведенные из центра вращения в точку приложения силы. Предполагается, что вектора сил лежат в плоскости, перпендикулярной оси вращения. Во всяком случае, понятно, что компонента силы, параллельная оси вращения, при закрепленной оси никакого вращательного действия произвести не может.
– радиус-вектора, проведенные из центра вращения в точку приложения силы. Предполагается, что вектора сил лежат в плоскости, перпендикулярной оси вращения. Во всяком случае, понятно, что компонента силы, параллельная оси вращения, при закрепленной оси никакого вращательного действия произвести не может.|
|
|
Разложим силу 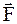 на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:
на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:
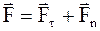 . (3.42)
. (3.42)
Вращательное действие силы определяется только касательной составляющей силы и положением точки приложения силы по отношению к центру вращения, т.е. радиусом 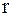 . Введем угол
. Введем угол  , образованный между направлениями векторов
, образованный между направлениями векторов 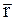 и
и 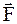 . Тогда получим
. Тогда получим
 (3.43)
(3.43)
Вращательное действие любой силы будет пропорционально произведению:
 или
или  . (3.44)
. (3.44)
Выражение 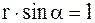 представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.
представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.
По правилу "рычага" равновесие наступает при равенстве
 . (3.45)
. (3.45)
Произведение  носит название момента силы относительно оси вращения
носит название момента силы относительно оси вращения  . Момент силы – это вектор, определяемый как векторное произведение:
. Момент силы – это вектор, определяемый как векторное произведение:
 . (3.46)
. (3.46)
Модуль  выражается следующим образом:
выражается следующим образом:
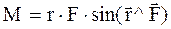 . (3.47)
. (3.47)
Этот вектор всегда перпендикулярен плоскости, образованной векторами 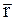 и
и 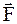 , т.е. направлен по оси вращения "по правилу правого винта". Поэтому в случае закрепленной оси вращения вместо векторного представления момента силы можно воспользоваться алгебраическим представлением. Если сила вращает тело по часовой стрелке, то момент силы будем считать положительным, если сила вращает тело против часовой стрелки, то моменту этой силы будем приписывать знак "минус". Заметим, что на рис.3.6 направление оси выбрано "от нас, за чертеж". Для сил
, т.е. направлен по оси вращения "по правилу правого винта". Поэтому в случае закрепленной оси вращения вместо векторного представления момента силы можно воспользоваться алгебраическим представлением. Если сила вращает тело по часовой стрелке, то момент силы будем считать положительным, если сила вращает тело против часовой стрелки, то моменту этой силы будем приписывать знак "минус". Заметим, что на рис.3.6 направление оси выбрано "от нас, за чертеж". Для сил 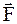 и
и 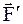 моменты равны
моменты равны 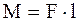 и
и  . Условие равновесия может быть записано как
. Условие равновесия может быть записано как
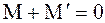 . (3.48)
. (3.48)
Силы 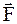 и
и 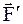 не вызывают вращение, если их моменты
не вызывают вращение, если их моменты  и
и  равны по величине и противоположны по направлению.
равны по величине и противоположны по направлению.
В общем случае, когда на тело действует 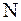 сил, рассматривают полный момент сил:
сил, рассматривают полный момент сил:
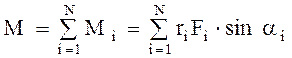 . (3.49)
. (3.49)
И условие равновесия тела с закрепленной осью вращения сводится к виду:
|
|
|
 . (3.50)
. (3.50)
Оказывается, что один и тот же момент внешней силы, действующей на различные тела (материальные точки), сообщает им различные угловые ускорения.
Для характеристики инертности тел (материальных точек) вращательному движению вводится в рассмотрение физическая величина, называемая моментом инерции материальной точки или тела (I относительно неподвижной оси (центра вращения). Чем больше  , тем меньше угловое ускорение e получит тело под действием данного момента силы
, тем меньше угловое ускорение e получит тело под действием данного момента силы  .
.
Моментом инерции материальной точки относительно какой-либо оси или центра вращения называется физическая величина, равная произведению массы материальной точки на квадрат расстояния от нее до оси или центра вращения:
DI = Dm×r2. (3.51)
Момент инерции тела - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Для тела с закрепленной осью вращения момент инерции представляет собой положительную скалярную величину.
Прямой способ вычисления момента инерции тела состоит в следующем: мысленно тело разбивают на совокупность материальных точек, записывают момент инерции 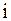 -й материальной точки, полный момент инерции получают суммированием элементарных моментов:
-й материальной точки, полный момент инерции получают суммированием элементарных моментов:
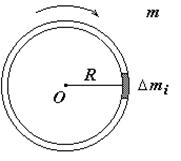 Рис.3.7 Рис.3.7
|
 или
или 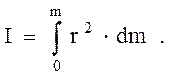 (3.52)
(3.52)
Рассмотрим несколько примеров:
 Рис.3.8
Рис.3.8
|
1. Момент инерции обруча, вращающегося вокруг собственной оси (рис.3.7). Обруч считаем "тонким" и однородным по плотности. В данном случае все материальные точки (элементарные массы) расположены на одинаковом расстоянии от оси вращения. Поэтому
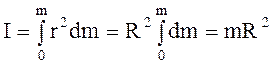 . (3.53)
. (3.53)
2. Момент инерции стержня относительно оси, проходящей перпендикулярно к нему через его середину (рис.3.8). Стержень считаем "тонким", однородным по сечению и распределению плотности. Длина стержня – 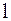 . Момент инерции материальной точки представим в виде дифференциала
. Момент инерции материальной точки представим в виде дифференциала
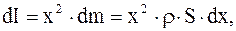 (3.54)
(3.54)
где 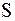 – площадь сечения.
– площадь сечения.
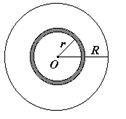 Рис.3.9
Рис.3.9
|
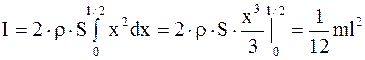 . (3.55)
. (3.55)
3. Момент инерции сплошного цилиндра относительно собственной оси (рис.3.9). Цилиндр (диск) считаем однородным по плотности. Радиус цилиндра – 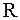 , длина –
, длина –  . В данном случае целесообразно разбить цилиндр на совокупность тонкостенных цилиндров, соосных друг с другом. Элементарный момент инерции представим в виде дифференциала
. В данном случае целесообразно разбить цилиндр на совокупность тонкостенных цилиндров, соосных друг с другом. Элементарный момент инерции представим в виде дифференциала
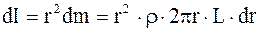 . (3.56)
. (3.56)
Момент инерции цилиндра получим путем интегрирования:
 . (3.57)
. (3.57)
4. Момент инерции шара относительно оси, проходящей через его центр, можно определить аналогично и вычисляется по формуле
 . (3.58)
. (3.58)
 Рис.3.10
Рис.3.10
|
Таким образом, момент инерции тела существенно зависит от его геометрии (формы), а также от положения оси вращения, т.е. зависит от распределения массы тела относительно оси вращения. Если выбрать новую ось вращения, оставив без изменения форму и размеры тела, то изменится и момент инерции тела. Поэтому определенный смысл момент инерции имеет только в том случае, когда задана ось вращения. Значительное упрощение в вычислениях момента инерции тела относительно оси, не проходящей через центр масс этого тела, можно получить, применяя теорему Штейнера, формулировку которой мы примем без доказательства (рис.3.10): «Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, I0 и произведения массы тела m0 на квадрат расстояния между осями», т.е.
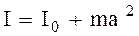 . (3.59)
. (3.59)
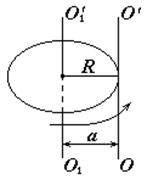 Рис.3.11
Рис.3.11
|
Примеры применения теоремы Штейнера:
1. Момент инерции диска относительно оси  , параллельной геометрической оси диска и проходящей через его край (рис.3.11).
, параллельной геометрической оси диска и проходящей через его край (рис.3.11).
Здесь  ,
,  . Поэтому
. Поэтому
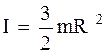 . (3.60)
. (3.60)
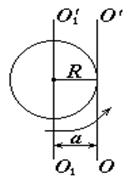 Рис.3.12
Рис.3.12
|
2. Момент инерции шара относительно оси, касательной к его поверхности (рис.3.12).
Здесь 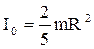 ,
, 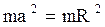 . Тогда
. Тогда
 . (3.61)
. (3.61)
3.5. Основной закон динамики вращательного движения
Мысленно разобьем тело с закрепленной осью вращения на совокупность материальных точек с массами 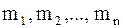 , каждая из них находится от оси вращения на расстоянии
, каждая из них находится от оси вращения на расстоянии 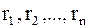 . На точку с индексом
. На точку с индексом 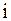 действует сила
действует сила
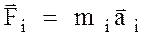 . (3.62)
. (3.62)
Интересуясь исключительно вращательным движением, удержим только касательную составляющую этой силы:
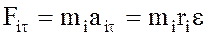 . (3.63)
. (3.63)
Итак,
 . (3.64)
. (3.64)
Умножим (3.64) на  , получим
, получим
 . (3.65)
. (3.65)
Но 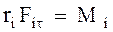 , поэтому момент силы, действующей на
, поэтому момент силы, действующей на 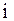 -ю материальную точку:
-ю материальную точку:
 . (3.66)
. (3.66)
Полный момент
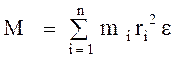 . (3.67)
. (3.67)
Введем обозначение 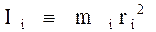 – момент инерции материальной точки относительно оси вращения.
– момент инерции материальной точки относительно оси вращения.
Момент инерции тела относительно оси вращения получим путем суммирования по всем материальным точкам данного тела:
 . (3.68)
. (3.68)
Тогда можно представить (3.67) в виде
 . (3.69)
. (3.69)
Или в векторном представлении
 . (3.70)
. (3.70)
Формулы (3.69) и (3.70) выражают основной закон динамики вращательного движения.
Выразим угловое ускорение из (3.70):
 . (3.71)
. (3.71)
Следовательно, угловое ускорение прямо пропорционально полному моменту сил, приложенных к данному телу, и обратно пропорционально моменту инерции тела относительно оси вращения.
Моментом импульса материальной точки относительно неподвижной оси (центра вращения) называется вектор L, равный векторному произведению радиус-вектора r, проведенного от оси (из центра вращения О) в место нахождения материальной точки, на вектор p ее импульса:
L = [ r´p ] =  [ r´ m v ], (3.72)
[ r´ m v ], (3.72)
где m - масса материальной точки; v - скорость материальной точки.
Моментом импульса системы (тела) относительно неподвижного центра вращения О называется геометрическая сумма L моментов импульса относительно той же точки О всех материальных точек системы:
 , (3.73)
, (3.73)
где r i, mi, v i - радиус-вектор, масса и скорость i-й материальной точки;
n - общее число этих точек в системе.
Если тело закреплено в точке О и его угловая скорость совпадает по направлению с вектором L, то момент импульса такого тела
L = I ω. (3.74)
Так как ε = d ω /dt, то
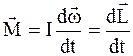 . (3.75)
. (3.75)
Формула (3.75) отображает общий вид второго закона динамики для тел, вращающихся относительно неподвижной оси; В данном виде он применим и для деформирующихся тел. При I = const формула (3.75) переходит в (3.70).
Основной закон динамики вращательного движения аналогичен второму закону Ньютона для материальной точки или тела, движущегося поступательно.
Можно указать также и закон, аналогичный третьему закону Ньютона: если одно тело действует на другое с некоторым вращающим моментом M 12, то всегда второе тело оказывает обратное воздействие на первое с вращающим моментом M 21, равным, но противоположно направленным:
M 12= - M 21. (3.76)
Из (3.75)
M× dt = d L. (3.77)
Произведение вращающего момента на время его действия M× dt называется импульсом вращающего момента. Импульс вращающего момента является вектором, ориентированным по направлению вектора M.
Пользуясь этими понятиями, второй закон механики для вращательного движения можно сформулировать следующим образом: импульс вращающего момента равен изменению момента количества движения тела, к которому приложен этот вращающий момент:
M× dt = d L = d×(I ω). (3.78)
3.6. Сопоставление формул динамики вращательного и динамики поступательного движений
Существует очень глубокая аналогия расчетных формул, основных понятий, физических параметров теории динамики поступательного и вращательного движения. Эта аналогия позволяет глубже понять физическую сущность параметров динамики вращательного движения. Сходство между понятиями и формулами двух динамик становится очевидным, если сопоставить их с помощью таблицы. В таблицу 3.2 вошли, помимо "чисто" динамических параметров и формул, параметры и формулы кинематики поступательного и вращательного движения.
Таблица 3.2
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 506; Нарушение авторских прав?; Мы поможем в написании вашей работы!