Аналитические методы

Рассмотрим два из них.

Метод последовательных приближений. Представим в уравнении (1) в виде отношения дифференциалов 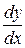, тогда

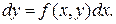
Далее, интегрируя обе части полученного соотношения на промежутке [ x₀, x ] получаем

,

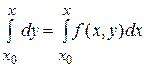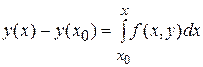
или

(3)

Соотношение (3) представляет собой интегральное уравнение, эквивалентное задаче (1), (2). На его основе строится следующий вычислительный процесс

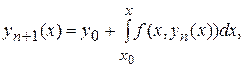(4)

где 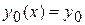, который и называется методом последовательных приближений. При определенных условиях последовательность функции 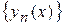сходится к точному решению задачи (1), (2). А именно,

Пусть в прямоугольнике 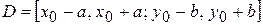выполнены условия теоремы существования и единственности и 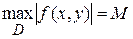. Тогда в промежутк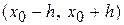е , где 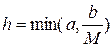последовательность (4) сходится к точному решению. Причем справедлива следующая оценка

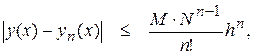
где .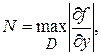

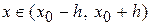Для иллюстрации этого метода рассмотрим следующий

Пример. Найти решение задачи Коши

, .

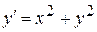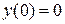Найти два первых приближения к решению, оценить погрешность.

Решение. Возьмем в качестве области 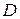квадрат [-1, 1; -1, 1]. Здесь 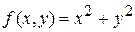, , 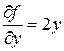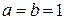. Тогда

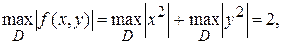
т.е. М=2,

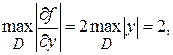
т.е. N=2,

.

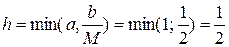Погрешность n -го приближения

,

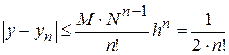отсюда погрешность второго,- .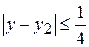

Найдем приближения 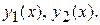Полагая, что 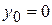, из (4) имеем

,

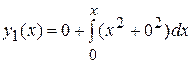т.е. .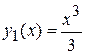

Тогда

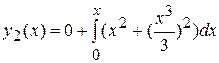
т.е.

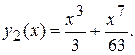
Замечание. В том случае, когда дана погрешность 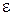приближенного решения число итераций, т.е. последовательных приближений, можно найти, потребовав

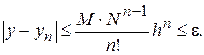
Так, например, в рассмотренном примере

,

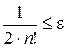откуда 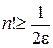и значение 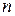устанавливается последовательным перебором.

Метод рядов Тейлора. В этом случае решение задачи (1), (2) ищется в виде ряда

.

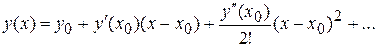Значения производных, необходимых для построения решения находятся путем последовательного дифференцирования уравнения (1). Так, непосредственно из него следует

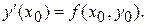
Далее,

,

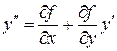тогда

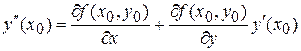
и т.д.

Очевидно, что данная процедура позволяет получить решение со сколь угодно высокой точностью лишь в том случае, когда функция 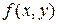является бесконечно дифференцируемой в точке 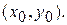В противном случае данный метод может быть вообще неприменим. См., например, задачу

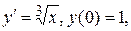
где 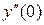уже не существует.

Дата добавления: 2014-01-06