Решение уравнений состояния методом Гаусса

Основным преимуществом метода Гаусса является наименьшее количество вычислительных операций по сравнению с другими методами решения систем линейных алгебраических уравнений. Суть этого метода заключается в последовательном исключении неизвестных.

К числу наиболее характерных вычислительных схем этого методы относятся алгоритмы с обратным ходом и без обратного хода.

В вычислительном отношении более эффективным является алгоритм метода Гаусса с обратным ходом. Практическая ценность алгоритма без обратного хода состоит в том, что на его основе может быть построен компактный алгоритм обращения матриц.

Решение системы n линейных алгебраических уравнений по методу Гаусса с обратным ходом состоит из двух этапов. На первом этапе (прямой ход) исходная система за n-1 однотипных шагов преобразуется таким образом, что матрица коэффициентов становится верхней треугольной, то есть все элементы, расположенные ниже ее главной диагонали, равны нулю. На втором этапе (обратный ход) последовательно определяются значения неизвестных.

Рассмотрим последовательность операций, выполняемых при прямом ходе.

На первом этапе в исходной системе уравнений

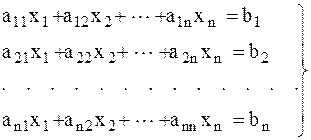
первое уравнений делится на a₁₁. Далее x₁ исключается из всех последующих уравнений (i = 2, 3 … n) путем умножения первого уравнения на a_i1 и вычитания из i-го уравнения. После выполнения этих операций получается система

уравнений с матрицей коэффициентов A ⁽¹⁾ :

A ⁽¹⁾ = ,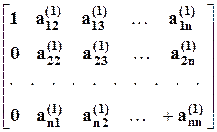

где ⁽¹⁾ – номер шага.

В результате система приводится к виду

Выполнение операций первого шага требует, чтобы элемент a₁₁, называемый ведущим, был отличен от нуля.

Второй шаг состоит в исключении x₂ из уравнений 3, 4 … n при использовании в качестве ведущего элемента 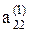. После второго шага система приводится к виду

Третий и последующий шаги выполняются аналогично.

Точность расчетов по методу Гаусса зависит от выбора ведущего элемента.

Может оказаться, что на некотором шаге ведущий элемент становится равным нулю (при точных расчетах) или же близким к нулю. В первом случае получить решение невозможно, во втором – погрешность дальнейших вычислений может быть чрезмерно велика.

Для уменьшения погрешностей расчета используется более сложная вычислительная схема, в которой на каждом шаге в качестве ведущего элемента выбирается наибольший по абсолютной величине элемент. Такая вычислительная схема называется схемой главного элемента. Реализация на ЭВМ схемы главного элемента требует более сложного программирования по сравнению с алгоритмом метода Гаусса с обратным ходом.

Рассмотрим в качестве примера решение системы уравнений 3-го порядка.

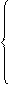
Первый шаг:

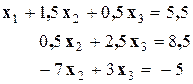
Второй шаг:

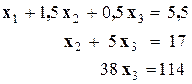
Третий шаг:

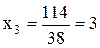
Далее выполняем вычисления, соответствующие обратному ходу:

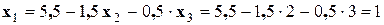
Дата добавления: 2014-01-06