Разложение Шеннона

Разложения функций по переменным

Законы алгебры логики

1. Законы коммутативности:

a Ù b = b Ù a, a Ú b = b Ú a.

2. Законы ассоциативности:

a Ù (b Ù с) = (а Ù b) Ù с, a Ú (b Ú с) = (а Ú b) Ú с.

3. Законы дистрибутивности:

a Ù (b Ú с) = (а Ù b) Ú (а Ù с), a Ú (b Ù с) = (а Ú b) Ù (а Ú с).

4. Законы идемпотентности:

а = a Ù а, a = а Ú a.

5. Законы нуля и единицы:

a Ù ù а = 0, а Ù 1 = а, a Ú ù а = 1, а Ú 0 = а.

6. Законы де Моргана:

ù (a Ú b) = ù a Ù ù b, ù (a Ù b) = ù a Ú ù b.

7. Законы поглощения:

a Ú (а Ù b) = а, a Ù (a Ú b) = а.

8. Законы склеивания:

(а Ú ù b) Ù (а Ú b) = а, (а Ù ù b) Ú (а Ù b) = а.

9. Закон двойного отрицания:

ù ù а = а.

Не все законы независимы друг от друга. Так, например, закон идемпотентности можно получить из закона поглощения с использованием законы дистрибутивности:

а = a Ú (а Ù b) = (a Ú а) Ù (а Ú b) = (a Ù (а Ú b)) Ú (a Ù (а Ú b)) = а Ú а.

Закон поглощения может быть выведен из закона нуля и единицы:

a Ú (а Ù b) = (a Ù 1) Ú (а Ù b) = a Ù (1 Ú b) = a Ù 1 = а.

Закон идемпотентности относительно дизъюнкции непосредственно выводится из законов нуля и единицы:

a Ú а = (a Ú а) Ù 1 = (а Ú а) Ù (ù а Ú а) = а Ú (ù а Ù а) = а Ú 0 = а.

При доказательствах логических выражений нужно всегда учитывать принцип двойственности. Так, вышеперечисленная цепочка равенств для закона поглощения может быть представлена следующим образом:

a Ù (а Ú b) = (a Ú 0) Ù (а Ú b) = a Ú (0 Ù b) = a Ú 0 = а.

Т.о. в качестве независимой системы законов можно выбрать законы: коммутативности, ассоциативности, дистрибутивности, нуля и единицы.

Введем следующие обозначения:

х⁰ = ù х; х¹ = х.

Пусть s - параметр, равный 0 или 1.

Тогда: х^s = 1, если х = s;

х^s = 0, если х ¹ s.

Теорема Шеннона: всякая логическая функция F (х₁, …, х_n) может быть представлена в виде:

F (х₁, …, х_m, х_m+1, …, х_n) = x₁ ^{s 1} … x_m ^{s m} F ( s ₁, …, s _m, х_m+1, …, х_n), (2.1)

где m £ n, а дизъюнкция берется по всем 2^mнаборам значений переменных х₁, …, х_m.

Это равенство называется разложением по переменным х₁, …, х_m.

{Пример: n = 4, m = 2.

Разложение будет иметь вид:

F (х₁, х₂, х₃ , х₄) = ù х₁ ù х₂ F (0, 0, х₃ , х₄) Ú ù х₁ х₂ F (0, 1, х₃ , х₄) Ú

Ú х₁ ù х₂ F (1, 0, х₃ , х₄) Ú х₁ х₂ F (1, 1, х₃ , х₄).

Доказательство.

Производим подстановкой в обе части (2.1) произвольного набора (s₁, …, s_m, s_m+1, …, s_n) всех n переменных.

Т.к. х^a = 1 только тогда, когда х = a, то среди 2 ^m конъюнкций x₁^a1 … x_m^am правой части (2.1) в единицу обратится только одна, в которой a₁ = s₁, …, a_m = s_m. Все остальные конъюнкции равны 0. Поэтому получим:

F (s₁, …, s_n) = s₁^s1 … s_m^sm F (s₁, …, s_m, s_m+1, …, s_n) = F (s₁, …, s_n).

Особое значение на практике имеет случай, когда m = n, т.е. разложение функции n переменных по n переменным:

F (х₁, …, х_n) = 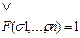x₁^s1 … x_n^sn.

Т.е. все переменные в правой части (2.1) получают фиксированное значение и функции в конъюнкциях правой части становятся равными 0 или 1. Т.о. дизъюнкция берется по всем наборам (s₁, …, s_n), на которых F = 1. Такое разложение называется СДНФ – совершенной дизъюнктивной формой функции F. СДНФ содержит ровно столько конъюнкций, сколько единиц в таблице истинности для F. Каждому единичному набору (s₁, …, s_n) соответствует конъюнкция всех переменных, в которой х_i взято с отрицанием, если s_i = 0, и без отрицания, если s_i = 1. Такие конъюнкции называются конституентами единицы. }

Дата добавления: 2014-01-06