Основные принципы построения формальных теорий исчисления

ФОРМАЛЬНЫЕ ТЕОРИИ

Переход от булевой алгебры к алгебре Жегалкина

Преобразование функций в алгебре Жегалкина

АЛГЕБРА ЖЕГАЛКИНА

Алгебра над множеством логических функций с двумя бинарными операциями: конъюнкцией (Ù), сложением по модулю 2 (Å) и константой единицы (1) называется алгеброй Жегалкина.

Здесь справедливы следующие законы:

1. коммутативный: x Å y = y Å x; x y = y x,

2. ассоциативный: x Å (y Å z) = (x Å y) Å z; x (y z) = (x y) z,

3. дистрибутивный: x (y Å z) = x y Å х z,

но: x Å (y z) ¹ (x Å y) (х Å z).

Действуют соотношения: х х = х,

x Å х = 0,

х 1 = х,

x Å 1 = ù х,

х 0 = 0,

x Å 0 = х.

Связь с булевым базисом осуществляется по следующим соотношениям:

x Å y = ù х y Ú x ù y;

х Ú y = ù (ù х ù y) = (x Å 1) (y Å 1) Å 1 = x y Å x Å y.

Если в СДНФ логической функции заменить операцию дизъюнкцию на операцию сложения по модулю 2, то равенство функций сохранится. В результате получим СПНФ – совершенную полиномиальную нормальную форму логической функции.

Пример: Дана СДНФ функции F = Ú (0, 3, 6).

Т.е. СДНФ: F = ù x₁ ù x₂ ù x₃ Ú ù x₁ x₂ x₃ Ú x₁ x₂ ù x₃.

Тогда СПНФ будет: F = ù x₁ ù x₂ ù x₃ Å ù x₁ x₂ x₃ Å x₁ x₂ ù x₃.

Если в СПНФ логической функции заменить все переменные с отрицанием по правилу ù х = x Å 1, раскрыть скобки и привести подобные по правилу x Å х = 0, то получим, так называемый, канонический полином Жегалкина в следующем виде:

a₀ Å a₁ x₁ Å a₂ x₂ Å a₃ x₁ x₂ Å … Å a_n x₁ x₂ x₃,

где а_i = (0, 1).

Пример: В нашем случае канонический полином Жегалкина будет:

F = (x₁ Å 1) (x₂ Å 1) (x₃ Å 1) Å (x₁ Å 1) x₂ x₃ Å x₁ x₂ (x₃ Å 1) =

= x₁ x₂ x₃ Å x₂ x₃ Å x₁ x₃ Å x₁ x₂ Å x₁ Å x₂ Å x₃ Å 1 Å

Å x₁ x₂ x₃ Å x₂ x₃ Å x₁ x₂ x₃ Å x₁ x₂ = x₁ x₂ x₃ Å x₁ x₃ Å x₁ Å x₂ Å Å x₃ Å 1.

Примечание: Для всякой логической функции существует канонический полином Жегалкина, и при этом, только один.

Математическая логика дает возможность изучения многих математических теорий в целом, оставаясь при этом неким «внешним» математическим аппаратом. Прежде всего математическую теорию уточняют и описывают при помощи строгого логико-математического языка. Этот процесс называется формализацией теории. Полученную в результате формализации теорию называют формальной.

1. Определяется некоторое счетное множество символов теории, называемое алфавитом теории. Конечная последовательность символов алфавита называется выражением.

2. Задается некоторое подмножество выражений, называемое формулами или правильно построенными выражениями.

3. Задается некоторое подмножество заведомо истинных формул, называемое аксиомами.

4. Задаются правила вывода как некоторое отношение на множестве формул.

Определение: Если формулы F₁, F₂, …, F_n, G находятся в отношении R, то говорят, что формула G непосредственно выводима из формул F₁, F₂, …, F_n, а отношение R (F₁, F₂, …, F_n, G) – правило вывода G из F₁, F₂, …, F_n. Этот факт записывается следующим образом:

F₁, F₂, …, F_n

R:

G

Формулы F₁, F₂, …, F_n, из которых выводится G, называются посылками, а формулы, которые выводятся (G), называются заключениями.

Определение: Выводом формулы В из формул А₁, А_2,, …, А_n называется последовательность формул F₁, F₂, …, F_m такая, что F_m = В, а любая формула F_i есть либо аксиома, либо одна из формул А₁, А_2,, …, А_n, либо одна из формул F₁, F₂, …, F_{i – 1}, полученных на предыдущих шагах вывода.

Факт выводимости обозначается:

А₁, А_2,, …, А_n В,

где А₁, А_2,, …, А_n – посылки, а В – заключение.

Определение: Доказательством формулы В формальной теории называется ее вывод из пустого множества формул, т.е. на основании только аксиом. Такая формула называется доказуемой в теории или теоремой.

Факт доказуемости записывается:

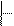В.

Примечание: присоединение посылок к формулам не нарушает их выводимости:

В,

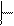А В.

Примечание: порядок посылок не имеет значения:

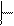А₁, А₂ В Û А₂, А₁ В.

Дата добавления: 2014-01-06