ПР-операторы

Оператор называется примитивно-рекурсивным (ПР), если он сохраняет примитивную рекурсивность функций, т.е. если результат его применения дает снова примитивно-рекурсивную функцию.

Операторы и являются ПР-операторами по определению.

Еще один ПР-оператор – оператор условного перехода , который по функциям и и предикату строит функцию

Существует теорема: если , и вычислимы по Тьюрингу, то разветвление 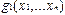и по также вычислимо.

В силу этой теоремы ПР-оператор 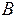вычислим по Тьюрингу.

Обобщение опреатора перехода на случай многозначного перехода по 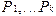, из которых истиннен всегда только один , также примитивно-рекурсивно.

Ограниченный оператор минимизации – применяется к предикатам.

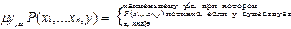
Из предиката 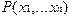с помощью оператора получается функция .

Ограничение z в операторе дает гарантию окончания вычислений, поскольку оно оценивает сверху число вычислений предиката .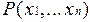

Если (ПР-оператор), то для вычисления f понадобится k+1 вычисление g и k вычислений h. В силу конечности общего числа операторов и 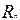, использованных для построения f из базисных функций, для любого k можно оценить количество элементарных действий для вычисления f.

Еще один ПР-оператор – оператор одновременной рекурсии – точнее целое семейство .

C его помощью строится рекурсивное описание сразу нескольких функций от (n-1)-ой переменной, причем значение каждой функции в точке y+1 зависит от значения всех функций в точке y.

По существу, совместная рекурсия дает рекурсивное описание функции-вектора.

Подведем некоторые итоги. Из простейших функций - константы 0, функции следования и функций тождества с помощью операторов суперпозиции и примитивной рекурсии может быть получено огромное разнообразие функций, включающих основные функции арифметики, алгебры и анализа (с поправкой на целочисленность). Следует сделать два замечания

1. Все примитивно-рекурсивные функции всюду опре-делены. Это следует из того, что простейшие функции всюду определены, а 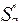и это свойство сохраняют.

2. Строго говоря, мы имеем дело не с функциями, а с их примитивно-рекурсивным описанием. Различие здесь имеет тот же смысл, что и различие между функциями и их представлением в виде формул.

Возникает вопрос: все ли функции являются примитивно-рекурсивными? Простые теоретико-множественные соображения пока-зывают, что нет.

Функция называется частично-рекурсивной, если она может быть построена из простейших функций: 0, х`,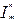 с помощью конечного числа применений 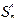, 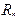и -оператора.

По определению -оператор применяется к предикатам. Поскольку в теории рекурсивных функций истинность предиката всегда связана со справедливостью некоторого равенства, то -оператору можно придать стандартную форму:

Будучи применен к вычислимой функции - оператор снова дает вычислимую функцию.

Однако эта процедура может не привести к результату: когда на данном наборе уравнение не имеет решения. В таком случае функция считается неопределенной.

Т.о. среди рекурсивных функций появляются неполностью опреде-ленные, т.е. частичные функции. Операторы над частичными функциями по-рождают новые частичные функции. При этом характер неопределенности может оказаться довольно сложным, а именно: для данного набора не най-дется способа установить определена ли на этом наборе и придется про-должать процесс вычисления неопределенное время, не зная, остановится он или нет.

Частично-рекурсивная функция называется общерекурсивной, если она всюду определена.

Дата добавления: 2014-01-06