
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление площадей плоских фигур. Вычисление объема тел вращения
|
|
|
|
Приближенное вычисление определенных интегралов.
Замена переменной и формула интегрирования по частям в определенном интеграле.
Формула Ньютона-Лейбница.
Свойства определенного интеграла.
Понятие определенного интеграла, его геометрический смысл.
ТЕМА 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
8. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА, ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
Пусть на отрезке  задана неотрицательная функция
задана неотрицательная функция  . Требуется найти площадь
. Требуется найти площадь 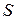 криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой  , прямыми
, прямыми 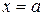 ,
,  и осью абсцисс
и осью абсцисс  (рис. 1).
(рис. 1).
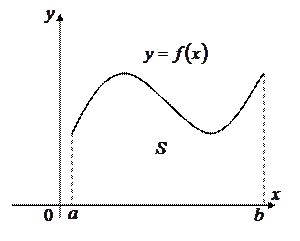
Разобьем отрезок  на
на  элементарных отрезков точками
элементарных отрезков точками 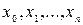 . На каждом отрезке
. На каждом отрезке 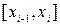 разбиения выберем точку
разбиения выберем точку 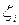 и положим
и положим 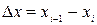 где
где  . Сумму вида
. Сумму вида

будем называть интегральной суммой для функции 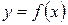 на
на  .
.
Каждое отдельное слагаемое интегральной суммы в этом случае равно площади  прямоугольника со сторонами
прямоугольника со сторонами 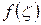 и
и 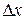 (рис. 2).
(рис. 2).
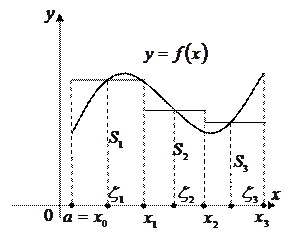
Для избранного разбиения отрезка  на части обозначим через
на части обозначим через 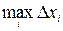 максимальную из длин отрезков
максимальную из длин отрезков 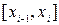 .
.
Определение. Пусть предел интегральной суммы 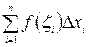 при стремлении
при стремлении  к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек  и точек
и точек  . Тогда этот предел называется определенным интегралом от функции
. Тогда этот предел называется определенным интегралом от функции  на
на  , обозначается
, обозначается  , а сама функция
, а сама функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке  , т.е.
, т.е.

При этом число  называется нижним пределом, число
называется нижним пределом, число 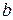 - верхним пределом; функция
- верхним пределом; функция  - подынтегральной функцией, выражение
- подынтегральной функцией, выражение 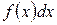 - подынтегральным выражением, а задача о нахождении
- подынтегральным выражением, а задача о нахождении  - интегрированием функции
- интегрированием функции  на отрезке
на отрезке  .
.
Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия: в то время как  представляет семейство функций,
представляет семейство функций,  есть определенное число.
есть определенное число.
Геометрический смысл определенного интеграла. Понятие определенного интеграла введено таким образом, что в случае, когда функция неотрицательная на отрезке  , где
, где 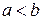 ,
,  численно равен площади под кривой
численно равен площади под кривой  на
на  .
.
|
|
|
Действительно при стремлении  к нулю сумма площадей
к нулю сумма площадей 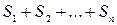 стремится к площади ограниченной под кривой
стремится к площади ограниченной под кривой 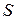 .
.
9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
1. Постоянный множитель можно выносить за знак интеграла:

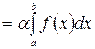
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:


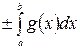
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей:
 =
=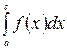 +
+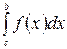
4. Если на отрезке  , где
, где 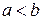 ,
, 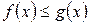 , то:
, то:


т.е. обе части неравенства можно почленно интегрировать.
5. Теорема о среднем. Если функция  непрерывна на отрезке
непрерывна на отрезке  , (где
, (где 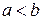 ), то найдется такое значение
), то найдется такое значение 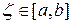 , что
, что

10. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА.
Теорема. Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и
и 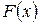 - любая первообразная для
- любая первообразная для  на
на  . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции  на
на  равен приращению первообразной
равен приращению первообразной 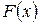 на этом отрезке, т.е.
на этом отрезке, т.е.


Нахождение определенных интегралов с использованием формулы Ньютона-Лейбница осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную 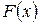 для подынтегральной функции
для подынтегральной функции  ; на втором применяется собственно формула Ньютона-Лейбница – находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений.
; на втором применяется собственно формула Ньютона-Лейбница – находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений.
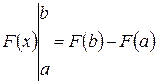 .
.
Пример 11.1. Вычислить: а)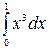 ; б)
; б)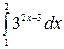
Решение:
а) Произвольная первообразная для функции 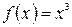 имеет вид
имеет вид 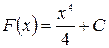 . Для нахождения интеграла по формуле Ньютона-Лейбница возьмем такую первообразную у которой
. Для нахождения интеграла по формуле Ньютона-Лейбница возьмем такую первообразную у которой  . Тогда:
. Тогда:
 .
.
б) Первообразную подынтегральной функции найдем используя формулу  . Применяя формулу Ньютона-Лейбница получаем:
. Применяя формулу Ньютона-Лейбница получаем:
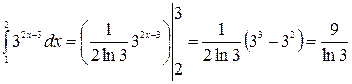
4. ЗАМЕНА ПЕРЕМЕННОЙ И ФОРМУЛА ИНТЕГИРОВАНИЯ ПО ЧАСТЯМ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.
|
|
|
Теорема 1. Пусть функция  имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 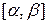 ,
, 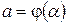 ,
, 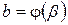 и функция
и функция  непрерывна в каждой точке
непрерывна в каждой точке 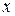 вида
вида  , где
, где 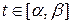 .
.
Тогда справедливо следующее равенство:
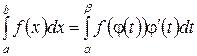
Эта формула носит название формулы замены переменной в определенном интеграле.
Пример 11.2. Вычислить:
а) 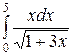 б)
б) 
Решение:
а) Воспользуемся заменой переменной 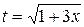 .
.
Тогда 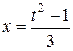 и
и 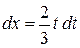 . Если
. Если  , то
, то 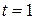 и, если
и, если 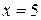 , то
, то  . Выполняя замену переменных получим:
. Выполняя замену переменных получим:
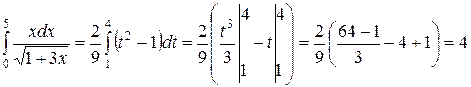
Отметим, что полагая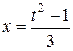 , можно также считать, что
, можно также считать, что  . При этом все условия теоремы 1 выполнены и, поскольку в этом случае
. При этом все условия теоремы 1 выполнены и, поскольку в этом случае 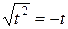 , получаем:
, получаем:
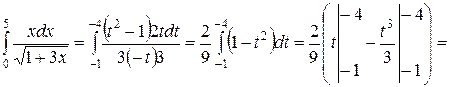
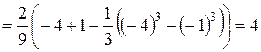
б) Положим 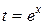 . Тогда
. Тогда 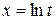 ,
, 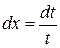 и, если
и, если 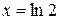 , то
, то  , и если
, и если 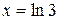 , то
, то 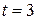 . Выполняя замену, получаем:
. Выполняя замену, получаем:
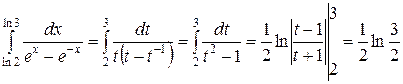
Теорема 2. Пусть функции 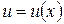 и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда:
. Тогда:
 ,
,
где 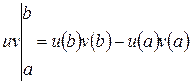 .
.
Формула  называется формулой интегрирования по частям для определенного интеграла.
называется формулой интегрирования по частям для определенного интеграла.
Пример 11.3. Вычислить 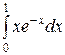 .
.
РЕШЕНИЕ:
Воспользуемся формулой интегрирования по частям: положим 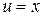 ,
,  . Тогда
. Тогда 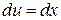 ,
,  получим:
получим:
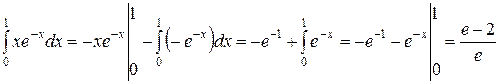
5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.
Важным средством вычисления определенных интегралов является формула Ньютона-Лейбница. Однако её применение на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае усложнения подынтегральной функции. Поэтому в приложениях используют так называемые численные методы, позволяющие найти приближенное значение искомого интеграла с требуемой точностью. Этот подход оказывается ещё более предпочтительным в связи с возрастающими возможностями вычислительной техники, реализующей алгоритмы с необходимой скоростью.
Рассмотрим одну из приближенных формул вычисления определенного интеграла – формулу трапеций.
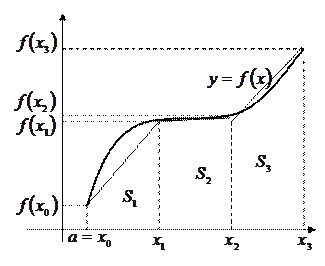 |
Пусть на отрезке
 задана непрерывная функция
задана непрерывная функция  . Предположим дополнительно, что
. Предположим дополнительно, что 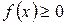 на
на  . Тогда
. Тогда 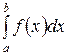 численно равен площади под кривой
численно равен площади под кривой  на отрезке
на отрезке  . Мы получим приближенное значение искомого интеграла, если вместо площади под кривой возьмем площадь под ломаной, расположенной достаточно близко к исходной кривой. Для построения этой ломаной поступим следующим образом: разобьем отрезок интегрирования на
. Мы получим приближенное значение искомого интеграла, если вместо площади под кривой возьмем площадь под ломаной, расположенной достаточно близко к исходной кривой. Для построения этой ломаной поступим следующим образом: разобьем отрезок интегрирования на  равных частей длиной
равных частей длиной 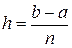 и на каждом из отрезков разбиения
и на каждом из отрезков разбиения  , где
, где 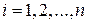 ;
; 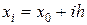 , заменим участок кривой
, заменим участок кривой  хордой, стягивающей концевые точки (рис.3)
хордой, стягивающей концевые точки (рис.3)
Рис. 3.
|
|
|
Тогда  , где
, где  - площади трапеций (площади под хордами на каждом из отрезков разбиения). И площади трапеций можно найти по формуле:
- площади трапеций (площади под хордами на каждом из отрезков разбиения). И площади трапеций можно найти по формуле:
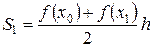 ;
; 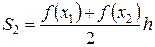 ,…,
,…, 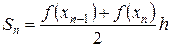
Тогда:
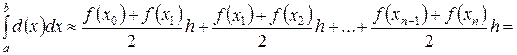
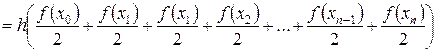 .
.
Вынося множитель 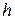 , заметим, что все слагаемые данной суммы, отличные от
, заметим, что все слагаемые данной суммы, отличные от 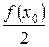 и
и  , встречаются в ней дважды. Приводя подобные и учитывая что
, встречаются в ней дважды. Приводя подобные и учитывая что 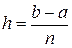 окончательно получаем:
окончательно получаем:
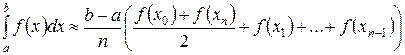 ,
,
где  ,
, 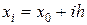 ,
,  . Окончательная формула носит название формулы трапеций. Она получена нами в предположении неотрицательности функции
. Окончательная формула носит название формулы трапеций. Она получена нами в предположении неотрицательности функции  , но можно также доказать, что этот результат остается справедливым также и в общем случае.
, но можно также доказать, что этот результат остается справедливым также и в общем случае.
6. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
В зависимости от того какого вида функция (неотрицательная, неположительная, общего вида) возможны различные варианты нахождения площадей плоских фигур.
1. Пусть функция  неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  . Тогда по геометрическому смыслу определенного интеграла площадь
. Тогда по геометрическому смыслу определенного интеграла площадь  под кривой
под кривой  на
на  численно равна определенному интегралу
численно равна определенному интегралу 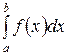 , т.е.
, т.е.
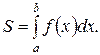
2. Пусть функция  неположительная и непрерывна на
неположительная и непрерывна на  . Отражая кривую
. Отражая кривую  относительно оси абсцисс, получаем кривую с уравнением
относительно оси абсцисс, получаем кривую с уравнением 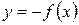 . Функция
. Функция 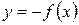 уже неотрицательна на
уже неотрицательна на  , а площадь под этой кривой на
, а площадь под этой кривой на  из соображений симметрии равна площади
из соображений симметрии равна площади 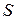 . Тогда
. Тогда
 , т.е.
, т.е.  .
.
3. Пусть на отрезке  задана непрерывная функция
задана непрерывная функция  общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция
общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция  будет знакопостоянна или равна нулю.
будет знакопостоянна или равна нулю.
Теорема. Пусть на отрезке  заданы непрерывные функции
заданы непрерывные функции 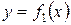 и
и 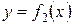 такие что
такие что 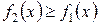 . Тогда площадь фигуры, заключенной между кривыми
. Тогда площадь фигуры, заключенной между кривыми 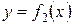 и
и 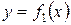 , на отрезке
, на отрезке  вычисляется по формуле
вычисляется по формуле
 .
.
Пример 11.4. Найти площадь фигуры, ограниченной линиями 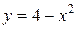 ,
,  .
.
РЕШЕНИЕ.
 |
Построим графики функций (рис. 4)
Координаты точек пресечения кривых найдем из системы уравнений:
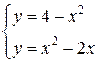
Решением будут координаты двух точек:  и
и 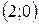 . Проецируя фигуру на ось абсцисс видим, что искомая площадь – это площадь фигуры, заключенной между кривыми; при этом на отрезке
. Проецируя фигуру на ось абсцисс видим, что искомая площадь – это площадь фигуры, заключенной между кривыми; при этом на отрезке 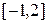
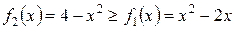 .
.
Применяем формулу  , получаем:
, получаем:
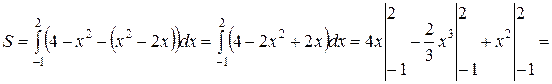
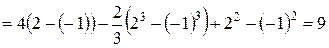
 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1330; Нарушение авторских прав?; Мы поможем в написании вашей работы!