График функции. Свойство монотонности функции

Понятие функции. Способы задания функций

Лекция 18. Числовые функции

План:

1. Определение числовой функции как частного случая соответствия.. Способы задания функции. Область определения и область значения функции.

2. График функции. Свойство монотонности функции

§ 9. ЧИСЛОВЫЕ ФУНКЦИИ

Функция - одно из важнейших понятий математики, исходное по­нятие ведущей ее области - математического анализа. В школьном курсе математики основное внимание уделяется числовым функциям. Причиной этого является тесная связь математики с естественными науками, в частности с физикой, для которой числовые функции слу­жат средством количественного описания различных зависимостей между величинами.

В начальном курсе математики понятие функции и все, что с ним связано, в явном виде не изучается, но идея функциональной зависи­мости буквально пронизывает его, а правильное понимание таких свойств реальных явлений, как взаимозависимость и изменяемость, является основой научного мировоззрения. Безусловно, все это требу­ет от учителя начальных классов определенных знаний о функции и ее свойствах, и прежде всего таких, которые помогут ему осуществлять в начальной школе пропедевтику понятия функции.

Выполним два задания для младших школьников.

1) Увеличь каждое нечетное однозначное число в 2 раза.

2) Заполни таблицу.

Уменьшаемое
Вычитаемое
Разность

С какими математическими понятиями мы имеем дело, выполняя эти задания?

Прежде всего, в каждом задании есть два числовых множества, меж­ду которыми устанавливается соответствие. В первом - это множества {1, 3,5, 7} и {2, 6, 10, 14}, а во втором - это множество значений вычи­таемого {0, 1, 2, 3, 4,5} и множество значений разности {5, 4, 3, 2, 1, 0}. В чем сходство устанавливаемых между этими множествами соответ­ствий? И в первом, и во втором задании каждому числу из первого множества сопоставляется единственное число из второго. В матема­тике такие соответствия называют функциями. В общем виде понятие числовой функции определяют так:

Определение. Числовой функцией называется такое соответст­вие между числовым множеством X и множеством R действи­тельных чисел, при котором каждому числу из множества X сопоставляется единственное число из множества R.

Множество X называют областью определения функции.

Функции принято обозначать буквами f, g, h и др. Если f - функция, заданная на множестве X, то действительное число у, соответствующее числу x из множества X, часто обозначают f (х) и пишут у = f (х). Переменную х при этом называют аргументом (или независимой переменной) функции f. Множество чисел вида f (х) для всех х из множества X называют областью значений функции f.

В рассмотренном выше первом примере функция задана на множестве X = {1, 3, 5, 7} - это ее область определения. А область значений этой функции есть множество {2, 6, 10, 14}.

Из определения функции вытекает, что для задания функции необходимо указать, во-первых, числовое множество X, т.е. область определения функции, и, во-вторых, правило, по которому каждому числу из множества X соответствует единственное действительное число.

Часто функции задают с помощью формул, указывающих, как по данному значению аргумента найти соответствующее значение функции. Например, формулы у = 2 х - 3, у = х ², у = 3 х, где х - действительное число, задают функции, поскольку каждому действительному значению х можно, производя указанные в формуле действия, поставить в соответствие единственное значение. у.

Заметим, что с помощью одной и той же формулы можно задать как угодно много функций, которые будут отличаться друг от друга областью определения. Например, функция у = 2 х - 3, где x € R, отлична от функции у = 2 х - 3, где х € N. Действительно, при х = -5 значение первой функции равно -13, а значение второй при х = -5 не определено.

Часто при задании функции с помощью формулы ее область определения не указывается. В таких случаях считают, что областью определения функции является область определения выражения f (х). Например, если функция задана формулой у = 2 х - 3, то ее областью определения считают множество R действительных чисел. Если функция задана формулой у = 6/(x -2), то ее область определения - есть множество R действительных чисел, исключая число 2 (если х = 2, то знаменатель данной дроби обращается в нуль).

Числовые функции можно представлять наглядно на координатной плоскости. Пусть у = f (х) - функция с областью определения X. Тогда ее графиком является множество таких точек координатной плоскости, которые имеют абсциссу х и ординату f (х) для всех х из множества X.

Так, графиком функции у = 2 х - 3, заданной на множестве R, является прямая (рис. 82), а графиком функции у = х², заданной также на множестве R - парабола (рис. 83).

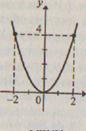
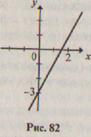
Рис. 83

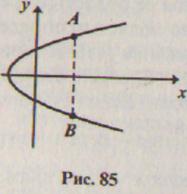
Функции можно задавать при помощи графика. Например, графи­ки, приведенные на рисунке 84, задают функции, одна из которых имеет в качестве области определения промежуток [-2, 3], а вторая конечное множество {-2, -1,0, 1,2,3}.

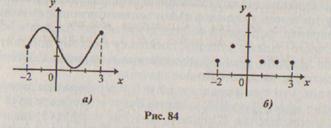
Не каждое множество точек на координатной плоскости представ­ляет собой график некоторой функции. Так как при каждом значении аргумента из области определения функция должна иметь лишь одно значение, то любая прямая, параллельная оси ординат, или совсем не пересекает график функции, или пересекает его лишь в одной точке. Если же это условие не выполняется, то множество точек координат­ной плоскости график функции не задает. На­пример, кривая на рисунке 85 не является гра­фиком функции - прямая АВ, параллельная оси ординат, пересекает ее в двух точках.

Функции можно задавать при помощи таблицы. Например, таблица, приведенная ниже, описывает зависимость температуры воздуха от времени суток. Эта зависимость - функция, так как каждому значению времени t соответствует единственное значение температуры воздуха р:

t (в часах)
p (в градусах Цельсия)	-3	-7	-5						-3

Числовые функции обладают многими свойствами. Мы рассмот­рим одно из них - свойство монотонности, так как понимание этого свойства учителем важно при обучении математике младших школь­ников.

Определение. Функция f (х) называется монотонной на некотором промежутке А, если она на этом промежутке возрастает или убывает.

Определение. Функция f (х) называется возрастающей на некотором промежутке А, если для любых чисел х₁, х₂ из множества А выпол­няется условие:

х₁ < х₂ ð f (х₁)< f (х₂)

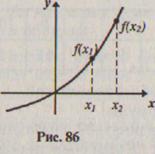
График функции, возрастающей на промежутке А, обладает осо­бенностью: при движении вдоль оси абсцисс слева направо по про­межутку А ординаты точек графика увеличиваются (рис. 86).

Определение. Функция f называется убывающей на некотором промежутке А, если для любых чисел х₁, х₂ из множества А выпол­няется условие:

х₁ < х₂ ð f (х₁)> f (х₂)

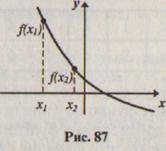
График функции, убывающей на промежутке А, обладает осо­бенностью: при движении вдоль оси абсцисс слева направо по про­межутку А ординаты точек графика уменьшаются (рис. 87).

Дата добавления: 2014-01-06