Лекция 2

Вопросы и упражнения к Лекции 1

1.Выразить связки ® и Ú через связки Ù и Ø. Убедиться в правильности через логические таблицы.

Ответ: [А®В=ØАÚВ=Ø(ØØАÙØВ)=Ø(АÙØВ)].

2. Тот же вопрос для пар связок ®, Ù и Ú,Ø.

3. Аналогичный вопрос для пар связок Ù,Ú и ®,Ø.

Ответ: [АÚВ=Ø(ØАÙØВ; АÙВ=Ø(А®В)].

4. А существует ли одна связка, через которую можно выразить все ранее приведённые?

Ответ: да, существует, и не одна! Это т.н. штрих Шеффера. См. Утверждение 2.3.3 ниже.

5. Что такое связанная переменная? Свободная переменная?

6. Может ли одна и таже переменная быть связанной и свободной в одном и том же выражении?

Классическое исчисление высказываний

2.1 Истинностные таблицы.

Придадим всему сказанному выше ещё более формальное описание. Пропозициональной переменной (пп) называется переменная, пробегающая над множеством высказывательных форм (в том числе и высказываний). Математическая логика очень часто использует определения объектов с помощью индуктивной процедуры, часто явно не указывая индуктивную переменную, которая обычно есть натуральное число. Доказательства также часто проводятся с использованием математической индукции, с помощью которой уже были построены объекты, являющиеся предметом доказательства. Поэтому рекомендуем читателю повторить метод математической индукции. Пропозициональная форма (пф) получается с помощью следующего индуктивного определения.

(i) любая пп есть пф; (ii) если А и В – пф, то (ØА), (АÙВ), (АÚВ), (А®В), (АºВ) есть пф; (iii) только те выражения есть пф, для которых это следует из пунктов (i) и (ii).

Понятно, что любому распределению истинностных значений пп, входящих в ту или иную пф, соответствует некоторое (определяемое с помощью истиностных таблиц) истинностное значение этой пф.

Поэтому всякая пф определяет некоторую истинностную функцию и м.б. функционально представлена таблицей. Например, форма АÚВ ® С может быть представлена такой таблицей:

А В С АÚВ АÚВ ® С

0 0 0 0 1

0 0 1 0 1

0 1 0 1 0

0 1 1 1 1

1 0 0 1 0

1 0 1 1 1

1 1 0 1 0

1 1 1 1 1

Упражнение. Составьте таблицу истинностности для (А®В)Ú(ØА);

Решение.

А В А®В ØА (А®В)Ú(ØА)

0 0 1 1 1

0 1 1 1 1

1 0 0 0 0

1 1 1 0 1

Введём ряд соглашений о более экономном употреблении скобок в записях пф. Внешнюю пару скобок в записи будем опускать. Если форма содержит вхождения только одной бинарной связки, то для любого вхождения этой связки опускаем внешние скобки у той из двух форм, соединяемых этим вхождением, которая стоит слева. Далее, связки упорядочим так: º, ®, Ú, Ù, Ø и будем опускать все те пары скобок, без которых возможно восстановление пф по правилу: Ø относится к наименьшей пф, следующей за ним, Ù связывает наименьшие формы, его окружающие; затем всякое вхождение Ú действует аналогичным образом (но после применения правила к Ø и Ù и т.д., включая ®, а затем º).Пример: А®В®С есть ((А®В)®С); АÚØВ®СºА есть (((АÚ(ØВ))®С)ºА).

Упражнение. Проверить, что различная расстановка скобок в формуле А®В®С даёт различные таблицы истинностности.

Отметим теперь, что если в пф имеется n различных пп, то возможны 2ⁿ различных распределений истинностнх значений для этих пп. Истинностная таблица для пф будет содержать столько же строк. Всего же различных пф, содержащих n пп, может быть только .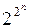

2.2 Тавтологии.

Пф, которая истинна независимо от того, какие значения принимают входящие в неё пп, называется тавтологией. Таким образом, функция истинности тавтологии принимает только значение 1. Говорят, что А логически влечет В, если пф А®В является тавтологией и что А логически эквивалентно В, если пф АºВ – тавтология. Каждая тавтология есть пример какого-либо логического закона. Например, АÚØА – закон исключённого третьего, (А®В) ® (ØВ®ØА) – закон контрапозиции и т.д. Отметим еще, что АÙ(А®В) логически влечёт В. Ясно, что таблицы истинностности дают эффективную процедуру для решения вопроса о том, является ли данная пф тавтологией.

Задача. Определить, являются ли следующие пф тавтологиями.

1.((А®В)®В)®В. 2. (АºВ)º(Аº(ВºА)). 3. (АºВ)º((А®В)Ù(В®А)).

Ответ: 1. Нет. 2. Нет. 3. Да. Указание: вычислите таблицы истинностности.

Отрицание тавтологии называется противоречием (т.е., если А – тавтология, то ØА – противоречие). Ясно, что противоречие есть пф, которой соответствует истинностная, всюду ложная, функция.

Задача. Приведите пять примеров пф, которые являются противоречиями. Указание: напишите пять примеров тавтологий и «навесьте» на них отрицание.

Высказывание (в любом естественном языке), которое м.б. получено из какой-либо тавтологии подстановкой любых высказываний вместо входящих в тавтологию пп (при этом, конечно, вместо одной и той же пп подставляется одно и то же высказывание), называется логически истинным и в этом случае истинность этого высказывания связана только с функциональным строением той пф, из которой это высказывание получено. Высказывание, которое получается аналогичным способом, но из противоречия, называется логически ложным. Установим теперь некоторые общие факты о тавтологиях.

Утверждение 2.2.1. Если А и А®В – тавтологии, то В – тавтология.

Замечание. Вы уже заметили, что в тексте все время не различаются собственно пп и пф и вместо тех и других используются одни и те же обозначения.

Доказательство: если А и А®В – тавтологии, то при любом распределении (фиксированном) истинностных значений входящих в них пп они принимают значение 1. Если бы В принимала при этом значение 0, то пф А®В принимала бы значение 0 также и мы получили бы противоречие. Следовательно, В принимает значение 1.

Замечание. Не лучшее доказательство. Попробуйте рассудить «более логично».

Утверждение 2.2.2. Если А – тавтология с пп А₁,…,А_n и пф В получается из пф А подстановкой пф В₁,…,В_n вместо пп выше, то пф В – также тавтология (подстановка в тавтологию любых пф приводит снова к тавтологии).

Докажите Утверждение 2.2.2 самостоятельно. Вспомните, что такое тавтология.

Утверждение 2.2.3 Если пф В₁ получается из пф А₁ подстановкой пф В вместо одного или большего числа вхождений пф А, то (АºВ)®(А₁ºВ₁) есть тавтология, т.е. из логической эквивалентности пф А и В следует логическая эквивалентность пф А₁ и В₁.

Доказательство 2.2.3. Т.к. АºВ, то подстановка В вместо А в любом вхождении А в А₁ не изменит таблицу истиностности последней, т.е. В₁ будет принимать те же значения истинности, что и А₁, что и даёт тавтологию формулы А₁ºВ₁.

2.3 Полные системы связок

Материал подобного сорта должен быть рассмотрен (обычно) в курсе «Дискретная математика», но иногда (а раньше – почти всегда) рассматривался и в курсе «Математическая логика». Поэтому мы будем кратки.

Утверждение 2.3.1. Всякая истинностная функция порождается некоторой пф, содержащей только связки Ø, Ù, Ú.

Утверждение 2.3.1 верно в силу того факта, что по данной истинностной функции можно написать совершенную конъюнктивную (или дизъюнктивную) нормальную форму (которая и есть требуемая пф).

Следствие 2.3.2 Для любой из трёх пар связок (Ø,Ù), (Ø,Ú) и (Ø,®) и для любой истинностной функции найдётся пф, содержащая только связки из заданной пары и порождающая данную функцию.

Для доказательства достаточно заметить, что любая из связок Ù, Ú, ® выражается через любую из остальных и Ø. Однако можно ввести и одну связку, с помощью которой можно добиться такого же эффекта.

Утверждение 2.3.3 Единственными бинарными связками, каждой из которых достаточно для построения всех истинностных функций, являются связки ¯ иô. Напишем таблицы истинностности для этих связок.

А В ¯ ô

1 1 0 0

0 1 0 1

1 0 0 1

0 0 1 1

Если связки р(А,В) достаточно для выразимости любой пф, то если р(1,1)=1 и Ø нельзя было бы выразить, т.е. р(1,1)=0. Совершенно аналогично, р(0,0)=1. Если второе и третье места есть 0,0 или 1,1 соответственно, то получим наши связки. Если же на этих местах стоят 0,1 или 1,0 соответственно, то формы р(А,В)ºØВ и р(А,В)ºØА оказываются тавтологиями и тогда р(А,В) выражена через Ø, а это не так (через Ø можно выразить либо тождественную истину, либо тождественную ложь).

Задачи.

1. Выразите через связки ¯, ôсначала Ù, а затем Ø.

2. Докажите, что ни одна из пар связок (Ù,Ú) и (Ø,º) не является достаточной для выражения всех истинностных функций (рассмотрите таблицы истинностности для соответствующих связок).

Указание.

А В А®В. Заметьте, что в последней строке напротив двух

1 1 1 нулей стоит 1 и получить ее с помощью только

0 1 1 связок Ú и Ù никак нельзя, т.е. ® нельзя выразить

1 0 0 через эти связки. Для другой пары связок дать

0 0 1 аналогичное рассуждение.

Приведём теперь ряд логических задач из книги Р. Смаллиана, которые можно решить с помощью составления логических таблиц, но рекомендуется решить с помощью логических рассуждений.

Предположим, что рыцарь – человек, который всегда говорит правду, что лжец – человек, который всегда лжёт и что нормальный человек иногда говорит правду, а иногда лжёт.

А) задачи про рыцарей и лжецов.

1. Трое людей А, В, и С разговаривали между собой. У А спросили: «Вы рыцарь или лжец?», на что А ответил очень неразборчиво. Тогда спросили у В «Что сказал А?». «А сказал, что он лжец»-ответил В. Но тогда С сказал, что В лжёт. Кто из островитян В и С рыцарь и кто – лжец? А кто такой А?

Ответ: В – лжец, С – рыцарь; установить, кто такой А - нельзя.

Решение. Сделаем сначала общее замечание по решению этой и

всех последующих задач: если в задаче несколько участников, то

нужно вычислить таблицу истинностных значений как булеву

функцию и проверить, какой вариант подойдёт. Но гораздо

интереснее рассудить логически.

Ни рыцарь, ни лжец не могут сказать «Я лжец». Поэтому В лжёт и

он лжец. Следовательно, С сказал правду и он рыцарь.

2. Из двух персонажей А и В нужно узнать, кто рыцарь, а кто лжец, если А сказал: «Среди нас есть лжец».

Ответ: А – рыцарь, В – лжец.

Решение. Если А – лжец, то высказанное утверждение ложно и оба рыцари, но это противоречит посылке и А – рыцарь и сказал истину, а тогда В – лжец.

3. А говорит: «Или я лжец, или В рыцарь». Кто из А и В есть кто?

Ответ: А и В оба рыцари.

Решение. По аналогии с предыдущей задачей. Но можно и

вычислить таблицу истинностности

4. Единственный персонаж А говорит: «Или я лжец, или снег всегда

чёрный». Какие выводы можно сделать?

Ответ: Составитель задачи – не рыцарь!!

Противоречивое условие задачи!!

5. А говорит: «Я лжец, а В – не лжец». Кто из них рыцарь, а кто –

лжец?

Ответ: А и В оба лжецы.

Решение. Если А рыцарь, то сказал бы правду, т.е. что он – лжец.

Следовательно, А – лжец. А тогда он солгал, но т.к. левая часть

Конъюнкции истинна, то должна быть ложна вторая часть, т.е. В –

тоже лжец.

6. Вы встречаете рыцаря или лжеца, помните, что его зовут то ли

Вася, то ли Витя, но не помните, как. Вы спрашиваете «Как Вас

зовут» и слышите в ответ «Витя». Как его зовут?

Ответ: Это нельзя определить, т.к. ни одна из четырёх комбинаций

из рыцарей и лжецов не подойдёт под условия задачи.

Б) задачи про рыцарей, лжецов и нормальных людей.

1. Из трёх людей один – рыцарь, другой – лжец и третий – нормальный человек. Они высказывают такие утверждения. А: «Я нормальный человек»; В: «А сказал правду»; С: «Я не нормальный человек». Кто такие А, В и С?

Ответ: Это лжец, нормальный человек и рыцарь в порядке следования.

Решение. А не может быть рыцарем и значит В сказал правду. Но если В – не нормальный человек (таким является А!!?) и он – рыцарь. Тогда С – лжец. Но лжец не может о себе сказать, что он – нормальный человек. Получили противоречие. Но тогда А – лжец!

Островитянин В тогда солгал и он – нормальный человек и, следовательно, С – рыцарь.

Замечание Если решать перебором, то рассматриваются 3´3=9 случаев. Совет: ещё раз медленно «пройдите» по решению.

2. Два человека высказывают такие утверждения. А: «В – рыцарь»;

В: «А – не рыцарь». Докажите, что хотя бы один из них говорит правду и что это не рыцарь. Разберите возможные случаи.

Решение. Раберём случаи.

а) Пусть А говорит правду. Тогда В – рыцарь и говорит правду. Тогда А – не рыцарь, т.е. А – лицо, говорящее правду, не являясь рыцарем.

в) Пусть А лжёт. Тогда В – не рыцарь, но В должен говорить правду, т.к. А не является рыцарем. Следовательно, В говорит правду, не будучи рыцарем.

3. Пусть А и В говорят. А: «В – рыцарь»; В: «А – лжец». Тогда либо

один из них говорит правду и это не рыцарь, либо один из них

лжёт и это не лжец.

Решение. Разберём случаи.

а) Если В говорит правду, то А – лжец и лжёт. Но тогда В – не рыцарь и говорит правду, не будучи рыцарем.

в) В лжёт, тогда А – не лжёт. Но говоря о В А заведомо лжёт, т.к. В не м.б. рыцарем, если не говорит правду. Следовательно, А лжёт, не будучи лжецом.

4. Пусть лжецы имеют минимальный ранг, нормальные люди –

средний и рыцари – высший ранг. Два человека говорят. А: «По рангу я ниже В». В: «Не правда». Можно ли определить ранг А или В? Можно ли установить истинностное значение каждого из двух утверждений?

Ответ: А и В – нормальные люди; высказывание А ложно, высказывание В истинно.

Вопросы и упражнения к Лекции 2.

1. Что такое таблица истинности?

2. Что такое пропозициональная форма, пропозициональная

переменная?

3. Что такое тавтология и противоречие?

4. Что такое полная система связок?

Дата добавления: 2014-01-06