Знакочередующиеся ряды

Вопросы

Знакопеременные ряды

Лекция 10

1. Каковы условия признака Лейбница? К каким рядам применяется признак Лейбница?

2. Дайте определение абсолютной сходимости.

3. Свойства абсолютно сходящихся рядов.

4. Приведите пример условно сходящегося ряда.

Определение. Знакочередующимся рядомназывается числовой ряд вида

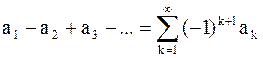(1)

или

,

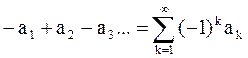где 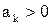для .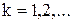

Для исследования сходимости таких рядов используется следующий признак.

Теорема 1. (Признак Лейбница).Пусть знакочередующийся ряд (1) удовлетворяет двум условиям:

а) ,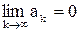

в) члены ряда по модулю убывают, т.е.

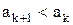, для .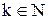

Тогда этот ряд сходится и его сумма 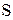удовлетворяет неравенству

.

Доказательство.Рассмотрим случай, когда ряд начинается с 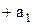; запишем частичную сумму для четного числа слагаемых

.

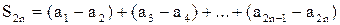Из условия в) теоремы следует, что 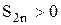и эта последовательность возрастает с ростом 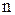(все скобки положительны). Запишем 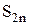другим способом.

.

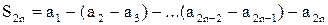Поскольку в скобках стоят положительные величины, то 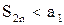. Возрастающая последовательность 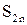ограничена сверху числом 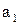, следовательно, согласно свойству пределов существует предел

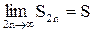и .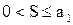

Для нечетного числа слагаемых, учитывая условие а), получим

,

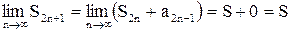т.е. в этом случае теорема доказана.

Случай, когда первый член ряда отрицателен, рассматривается аналогично.

Пример1. Исследуем сходимость знакочередующегося ряда

.

Поскольку 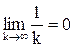и 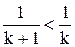, для всех , то этот ряд сходится, и его сумма 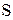удовлетворяет неравенству

.

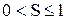На самом деле, можно проверить, что .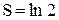

Введем еще одно важное понятие для сходящегося ряда.

Определение. n-ым остатком сходящего ряда (1) называется разность между его суммой S и частичной суммой :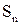

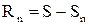. (10.11)

Этот остаток есть сумма членов ряда, начиная с 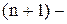го

.

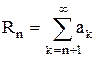Из (1) следует, что остаток можно определить только для сходящегося ряда, и что

,

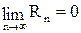т.к.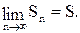

Следствие. Остаток знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, по модулю не превосходит модуля своего первого члена, т.е.

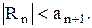
Доказательство этого факта следует из того, что остаток является суммой знакочередующегося ряда, удовлетворяющего условиям признака Лейбница

или .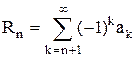

Этот факт позволяет наиболее просто определять количество слагаемых ряда для приближенного вычисления его суммы. В случае, если ряд не удовлетворяет условиям теоремы Лейбница, эта оценка обычно более трудоемка.

Пример2. Вычислить с погрешностью, не превосходящей 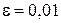сумму ряда

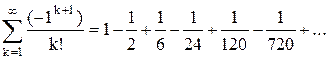
Очевидно, что ряд удовлетворяет условиям теоремы Лейбница.

Поскольку у этого ряда

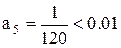, то 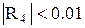. Отбросив этот остаток из суммы ряда, получим, что с требуемой точностью

.

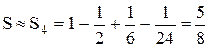2.Знакопеременные ряды. Абсолютная и условная сходимость рядов.

Пусть имеется произвольный числовой ряд:

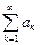(1)

и ряд, составленный из абсолютных величин его членов,

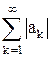. (2)

Определение. Ряд (1) называется абсолютно сходящимся, если сходится ряд (2). Если ряд (1) сходится, а (2) расходится, то ряд (1) называется условно сходящимся.

Пример3. Ряд 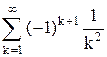сходится абсолютно, так как сходится ряд из абсолютных величин членов этого ряда (это ряд Дирихле с ).

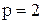Дата добавления: 2014-01-06