Логические Исчисления

3.1 Исчисления высказывания (ИВ).

3.1.1 Опр.еделения.

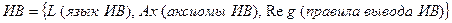
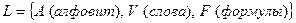
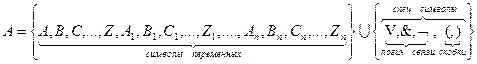
Опр.: V – словом в алфавите А, называется любая конечная упорядоченная последовательность его букв.

Опр.: Формативная последовательность слов – конечная последовательность слов и высказываний 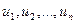, если они имеют формат вида:

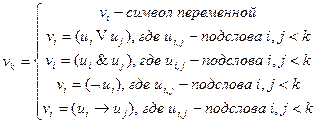
Опр.: F – формулой ИВ, называется любое слово, входящее в какую-нибудь формативную последовательность.

Пример: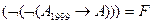

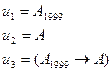
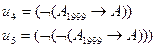
Опр.: Аксиомы – специально выделенное подмножество формул.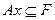

1)

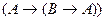
2)

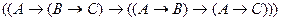
3)

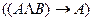
4)

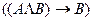
5)

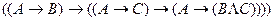
6)

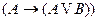
7)

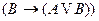
8)

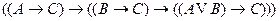
9)

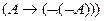
10)

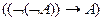
11)

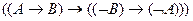
Reg – правила вывода ИВ (некоторые правила преобразования первого слова в другое).

a – символ переменной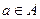

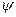- произвольное слово ИВ (формула)

Отображение 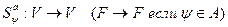действует так, что на место каждого вхождения символа а, пишется слово .

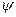Пример: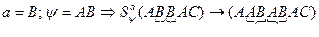

Правило modus ponens: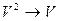

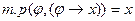
3.1.2 Формальный вывод.(простейшая модель доказательства теоремы)

Опр.: Последовательность формул ИВ, называется формальным выводом, если каждая формула этой последовательности имеет следующий вид:

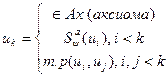
Опр.: Выводимый формулой (теоремой) ИВ называется любая формула входящая в какой-нибудь формальный вывод. 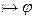- выводимая формула ИВ.

Пример: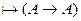

1)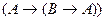
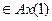
2)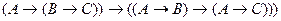
3)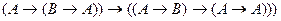
4)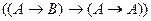
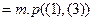
5)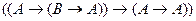
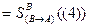
6)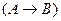

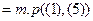
Правило одновременной подстановки.

Замечание: Если формула 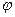выводима, то выводима и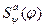

Возьмем формативную последовательность вывода 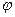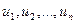и добавим в неё 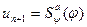, получившаяся последовательность является формальным выводом.

(Если выводима 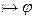то если 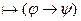, то выводима )

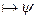Теор: Если выводимая формула 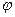, то 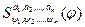(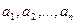- различные символы переменных) выводима

Выберем 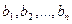- символы переменных которые различны между собой и не входят не в одну из формул 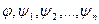, сделаем подстановку 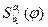и последовательно применим 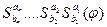и в новом слове делаем последовательную подстановку: 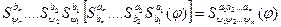, где 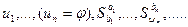- является формальным выводом.

3.1.3 Формальный вывод из гипотез.

Опр.: Формальным выводом из гипотез 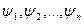(формулы), называется такая последовательность слов 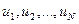, каждая из которых удовлетворяет условию:

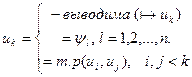
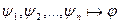если формулу 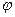можно включить в некоторый формальный вывод из гипотез .

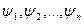Лемма: 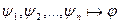; 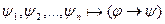: то тогда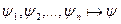

Напишем список:

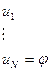
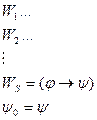
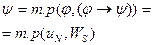
Лемма: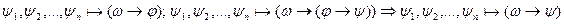

Док: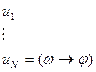

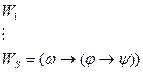
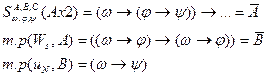
3.1.4 Теорема Дедукции.

Если из

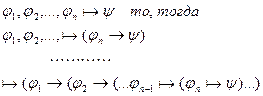
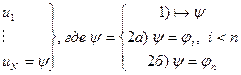
1) и 2а) 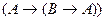, где 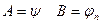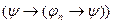по правилу m.p. 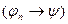, ч.т.д.

2б) 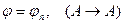- уже выводили 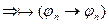, ч.т.д.

Базис индукции: N=1 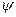- формальный вывод из длинного списка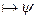

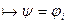(только что доказано), осуществим переход по индукции:

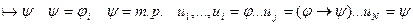
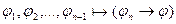по индукции

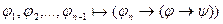и по лемме 2

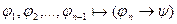
Пример: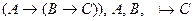

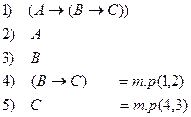по теореме дедукции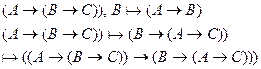

3.2 Критерий выводимости в ИВ.

3.2.1 Формулировка теоремы.

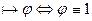- тавтология

при любой интерпретации алфавита (символов переменных)

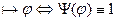
3.2.2 Понятие интерпретации.

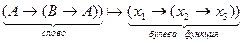
символ переменной 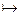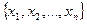переменную поставим в соответствие.

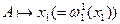, где 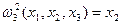- проекция на .

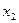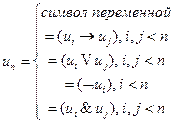
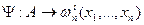
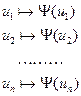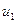; - только символ

переменных, т.к.

это заглавное слово

формативной последо-

вательности вида:

Где: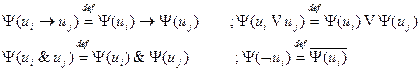

3.2.3 Доказательство теоремы.

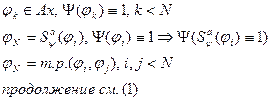
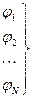
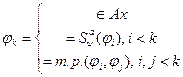формальный

вывод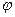

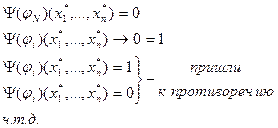
(1)

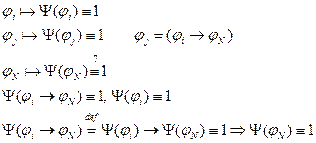
3.3 Непротиворечивость ИВ.

3.3.1 Опр.еделение.

1) ИВ противоречиво, если формула А выводима в нем. .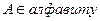

2) 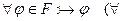формула выводима в ИВ)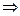ИВ противоречиво.

3) 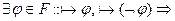ИВ противоречиво.

ИВ непротиворечиво, если оно не является противоречивым.

Теорема: ИВ является непротиворечивым исчислением по отношению к любому из трех Опр.еделений.

Док-во: (1) Если 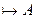, то соответствующая ей булева функция будет тождественно равна 1.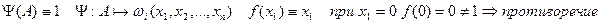

(2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.

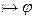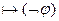
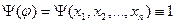(3) Пусть и - булева функция

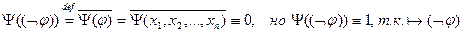- противоречие.

3.4 Формальные исчисления.

Алфавит – конечное или счетное множество символов, возможно, разбитых на группы. Алфавит должен быть упорядоченным множеством.

Слово – конечная упорядоченная последовательность символов алфавита, в т.ч. пустое слово.

V – множество всех слов.

Вычислимая функция от нескольких натуральных переменных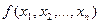

(f – может быть не всюду Опр.еделенной)

f – называется вычислимой, если 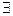такая машина Тьюринга, которая её вычисляет.

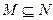- разрешимое множество, если характеристическая функция

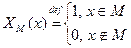- является вычислимой.

Множество 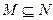называется перечислимым, если 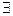такая вычислимая функция

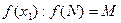
М - разрешимо 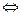М и N \ M перечислимы.

М – перечислимо 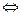М – область Опр.еделения некоторой вычислимой функции.

Множество всех формул F – некоторое разрешимое подмножество V.

Т – счетное множество, если 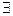его биективное отображение на V.

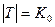- обозначение счетного множества. (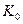- алеф-нуль)

Если 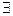и зафиксировано биективное и вычислимое отображение 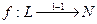(вычис.),

то L – ансамбль.

V – ансамбль (слова лексикографически упорядочены и занумерованы)

Опр.еделение: В произвольном формальном исчислении: 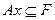- множество всех аксиом – разрешимое подмножество множества всех формул.

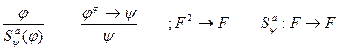
Правило вывода:

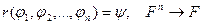,при 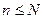разрешимо. Для ИВ N =2.

Пример:

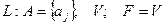
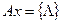(пустое слово),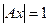

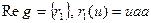
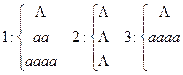1 и 2 – формальные выводы.

3 – не является формальным выводом.

Дата добавления: 2014-01-06