
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение следов плоскости
|
|
|
|
Каждый след плоскости представляет собой прямую линию, для построения которой необходимо определить две ее точки (одной из них может служить точка схода следов на оси проекций). Если известно направление следа плоскости, достаточно построить одну точку, принадлежащую искомому следу.
На рис. 3.12 показано построение следов плоскости, заданной треугольником ВСD. Горизонтальный след плоскости определен построением горизонтальных следов М1 и М2 прямых BC и CD, принадлежащих плоскости.
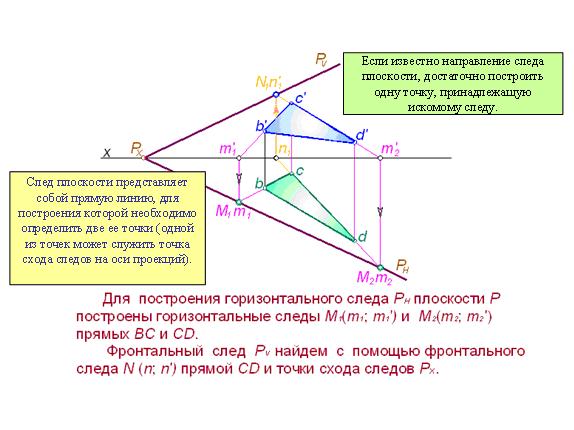
Рис. 3.12
Фронтальный след плоскости построен с помощью определения одного фронтального следа N1 прямой CD и использования в качестве второй точки - точки схода следов РХ.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2554; Нарушение авторских прав?; Мы поможем в написании вашей работы!