Закон сохранения импульса и его векторный характер

Рассмотрим произвольную систему, состоящую из N попарно взаимодействующих материальных точек. Введем обозначение для силы, действующей на материальную точку с номером i со стороны точки с номером k - 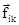. Кроме сил взаимодействия, которые являются внутренними, на каждую материальную точку могут действовать силы со стороны объектов, не входящих в данную систему. Результирующую внешнюю силы, действующую на материальную точку с номером i, обозначим .

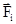Движение каждой из материальных точек системы можно описать на основании второго закона Ньютона:

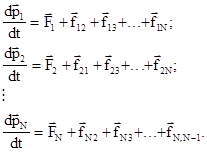
Сложим, соответственно, левые и правые части этих уравнений движения. В силу парности взаимодействия частиц системы и на основании третьего закона Ньютона 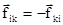. Поэтому

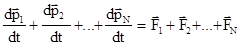
или

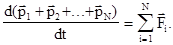(3.1)

Определение: Импульсом системы материальных точек 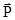называется векторная сумма импульсов всех материальных точек системы, то есть

(3.2)

Из определения импульса системы частиц следует, что эта величина является векторной и обладает свойством аддитивности.

Соотношение (3.1) с учетом определения (3.2) примет вид

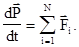(3.3)

Из этого соотношения непосредственно следуют важнейшие следствия:

- Импульс системы материальных точек, как целого, может измениться только в результате действия внешних сил. Отсутствие или наличие взаимодействия между частицами системы и его характер не влияет на движение системы как целого.

- Скорость изменения импульса системы равна векторной сумме внешних сил, действующих на материальные точки системы.

- Если на систему частиц не действуют внешние силы, то есть все 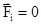(замкнутая система), или сумма внешних сил равна нулю, то импульс системы частиц остается постоянным, независимо от характера взаимодействия частиц системы между собой

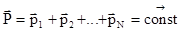. (3.4)

Последнее следствие носит название закона сохранения импульса. Несмотря на то, что обоснование закона сохранения импульса получено на основании классических законов Ньютона, обладающих ограниченной областью применения, утверждение, что импульс изолированной системы есть величина постоянная, является фундаментальным законом природы. Он справедлив как в релятивистской, так и в квантовой механике, хотя понятия импульса и меры взаимодействия там имеют другое содержание.

Иногда при решении практических задач классической динамики систем материальных точек встречаются случаи, когда существует такое направление (например ОX), вдоль которого алгебраическая сумма проекций внешних сил равна нулю. Тогда непосредственно из (3.3) следует, что вдоль этого направления сохраняется алгебраическая сумма проекций импульсов системы частиц, то есть

.

Часто для описания движения системы, как целого, удобно использовать понятие центра инерции (центра масс).

Центром инерции (центром масс) системы материальных точек называется особая точка, положение которой определяется радиус - вектором:

(3.5)

Если при движении частиц системы их массы остаются постоянными, то скорость центра масс определяется соотношениями:

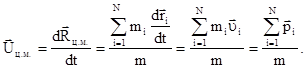
Последнему из этих равенств можно придать следующий вид, учитывая (3.2):

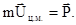(3.6)

Таким образом, импульс системы частиц, как целого, определяется общей массой системы и скоростью ее центра масс. Другими словами, импульс системы равен импульсу материальной точки, масса которой равна общей массе системы, а скорость равна скорости центра масс системы.

С помощью (3.6) уравнение движения системы точек (3.3), как целого, можно записать в виде

(3.7)

Последнее равенство означает, что центр масс системы движется как материальная точка с массой, равной массе всей системы, к которой приложена сила, равная векторной сумме внешних сил, действующих на материальные точки системы.

В частности, для замкнутой системы центр ее масс либо покоится, либо движется равномерно и прямолинейно.

Понятие центра масс особо полезно при описании поступательного движения твердого тела.

Действительно, поскольку твердое является частным случаем системы взаимодействующих между собой частиц, которые, согласно п.п. 1.2. и 1.5, при поступательном движении движутся одинаково, то достаточно описать с помощью (3.6) и (3.7) движение центра масс твердого тела. При этом необходимо считать, что масса m твердого тела сосредоточена в центре масс, к которому приложена равнодействующая всех внешних сил, действующих на это тело.

Часто взаимодействие материальных точек носит характер удара, когда время взаимодействия очень мало. Обычно в таких ситуациях изменение импульсов материальных точек, вызванное таким взаимодействием, значительно превышает изменение импульсов за счет действия внешних сил во время удара. В этом случае соударяющиеся частицы можно с высокой степенью точности считать замкнутой системой и за время удара применять закон сохранения импульса.

Предельными случаями ударов являются абсолютно упругий и абсолютно неупругий удары. Результаты подобных ударов обсуждаются ниже (см. п.3.8.2).

Замечание: В соотношениях (3.3) и (3.7) векторную сумму внешних сил нельзя понимать, вообще говоря, как равнодействующую силу, так как эти силы действуют на разные материальные точки системы.

Вывод: Закон сохранения импульса является фундаментальным законом природы и содержит в себе утверждение:

Дата добавления: 2014-01-07