Оптимизация технологических процессов с применением методов линейного программирования

Задачи исследования операций в условиях неопределенности

В некоторых задачах значения отдельных параметров остаются неизвестны исследователю. Это могут быть факторы, связанные с характеристиками сырья, влиянием природных условий; характером спроса и требований к продукции и т. д. Подход к решению таких задач зависит, прежде всего, от вида неопределенности. В наиболее благоприятной ситуации неопределенность имеет вероятностную природу. Это означает, что неизвестные параметры представляют собой случайные величины, значения которых можно оценить хотя бы принципиально по результатам многократных наблюдений, проводимых в одних и тех же условиях. В этом случае говорят о статистической устойчивости явления и решают задачу с применением хорошо разработанных методов теории вероятности и математической статистики. Таковы, например, задачи теории надежности, массового обслуживания, управления запасами при случайном спросе. Задачи оптимизации, содержащие случайные факторы, изучаются в теории стохастического программирования.

Иногда допустимо пренебречь вероятностной природой неизвестных факторов, заменив их значения оценками соответствующих математических ожиданий. Тогда задача сводится к детерминированной. Так поступают, как правило, с эмпирическими моделями. Для них значения отклика, полученные на основании опытных данных, являются случайными величинами. По результатам обработки эксперимента методом регрессионного анализа отыскивают зависимость оценки математического ожидания отклика от варьируемых факторов, с которой в дальнейшем работают как с детерминированной моделью.

Сложнее ситуации, когда исключена возможность применения статистических методов из-за отсутствия статистической устойчивости явления. Примером может служить характер спроса на отдельные виды продукции на внешнем рынке, подверженный влиянию многих факторов разной природы. Подобными задачами занимается теория принятия решений.

Возможны случаи, когда неопределенность в постановке задачи исследования операций связана с действиями противника, преследующего цели, полностью или частично противоположные нашей. Это прежде всего задачи, имеющие военные приложения, а также ситуации, предполагающие конкурентную борьбу. Математические модели таких задач рассматриваются в теории игр.

5.5.1. Примеры моделей и общая постановка задачи линейного
программирования

Задачи линейного программирования (ЗЛП) составляют большой класс задач исследования операций. К ним сводятся многие задачи распределения ресурсов: оптимальной загрузки станков, формирования производственной программы, планирования раскроя материалов и ряд других.

Особенность структуры ЗЛП состоит в том, что критерий оптимальности в них линейно зависит от элементов решения, а условия функционирования объекта записываются в виде линейных равенств или неравенств относительно этих переменных. Такие ограничения называются линейными.

Рассмотрим несколько примеров задач линейного программирования.

Задача формирования производственной программы. Мебельная фабрика выпускает три вида изделий: шкафы, столы и стулья. В производстве применяется оборудование трех типов: фрезерные, сверлильные и шлифовальные станки. Известны нормы времени работы для каждого типа оборудования при изготовлении одного изделия каждого вида (табл. 5.1).

Таблица 5.1
Изделие	Фрезерные станки	Сверлильные станки	Шлифовальные станки
Шкафы	0,25	0,18	0,24
Столы	0,20	0,13	0,19
Стулья	0,30	0,11	0,14

Согласно плановому заданию должно быть изготовлено не менее 150 шкафов, 200 столов и 400 стульев. Фабрика получает прибыль за изготовление одного шкафа в размере 5 у.е., стола – 3 у.е. и стула – 2 у.е. Известен ресурс рабочего времени фрезерных станков – 250 ч, сверлильных станков – 300 ч, шлифовальных станков – 320 ч. Требуется определить количество выпускаемых изделий, при котором план по каждому виду продукции выполнен, ресурсы по всем видам оборудования не превышены, а полученная прибыль максимальна.

Составим математическую модель этой задачи. Обозначим через 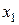количество изготавливаемых фабрикой шкафов, 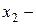столов, 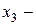стульев. Тогда требование выполнения плана запишется в виде неравенств:

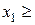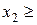150; 200; 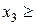400. (5.2)

Неравенства (5.2) представляют собой ограничения, обеспечивающие выполнение планового задания. Найдем выражение для длительности работы фрезерных станков. В процессе изготовления одного шкафа такой станок работает 0,25 ч (см. табл. 5.1). Длительность работы этих станков при изготовлении 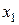шкафов равна 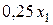ч. Аналогично, при изготовлении всех столов затрачивается 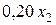ч, всех стульев 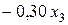ч машинного времени фрезерных станков. Всего затраты машинного времени по фрезерным станкам составляют 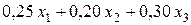ч. Поскольку суммарное время работы этого оборудования не должно превышать 250 ч, то ограничение по ресурсам машинного времени для фрезерных станков следует записать в виде неравенства

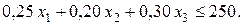(5.3)

Подобным же образом легко составить аналогичные ограничения для сверлильных и шлифовальных станков. Они имеют вид соответственно

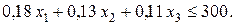(5.4)

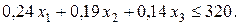(5.5)

Рассмотрим зависимость критерия оптимальности от переменных математической модели. Эта зависимость носит название целевой функции. В нашем примере критерием является прибыль.

Величина прибыли от изготовления 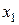шкафов равна 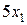у.е., от изготовления 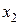столов 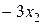у.е., от изготовления 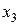стульев 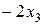у.е. Целевая функция таким образом имеет вид 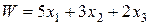. Требование достижения ее максимума записывают в виде

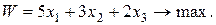(5.6)

Таким образом, математическая модель данной задачи состоит из целевой функции (5.6) и ограничений (3.2)... (3.5). Существенно, что как целевая функция, так и левые части ограничений являются линейными функциями переменных 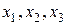, т. е. многочленами 1-го порядка. Поэтому составленная модель относится к классу задач линейного программирования.

Теперь задаче формирования производственной программы мебельной фабрики можно дать следующую математическую формулировку: требуется найти значения переменных 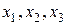, при которых функция (5.6) обращается в максимум и выполняются неравенства (3.2)... (3.5).

Задача оптимального раскроя. Плиты размером 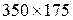см подлежат раскрою на заготовки двух типоразмеров: 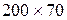см и 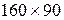см. Требуется получить не менее 300 заготовок первого и не менее 400 заготовок второго типоразмера. При этом суммарное (по площади) количество отходов должно быть минимально.

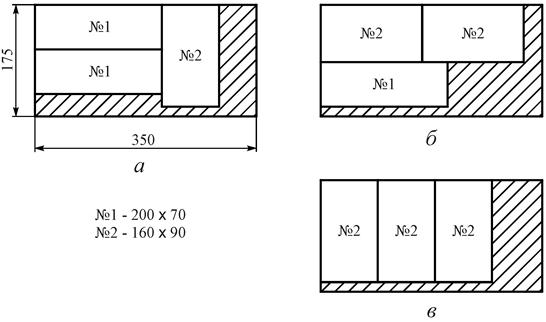
Рассмотрим все возможные варианты раскроя. На рис. 5.1, а показан вариант раскроя плиты на две заготовки 1-го и одну заготовку 2-го типоразмера, площадь отходов равна 18850 см². Часть плиты, уходящая в отходы, заштрихована. Все другие варианты, содержащие эти же три заготовки, различаются только их расположением на плите и эквивалентны с точки зрения экономичности.

Рис. 5.1. Варианты раскроя древесностружечной плиты

По варианту раскроя на рис. 5.1, б можно получить одну заготовку 1-го и две заготовки 2-го типоразмера, площадь отходов равна 18450 см². По третьему варианту раскроя получают три заготовки 2-го типоразмера (рис. 5.1, в) с площадью отходов 18050 см².

Для решения задачи следует выяснить, сколько плит надо раскроить по каждому из рассмотренных вариантов при выполнении предъявляемых требований. Обозначим через 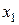количество плит, раскраиваемых по первому варианту, через 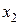по второму и через 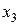по третьему. Составим ограничение по выпуску заготовок 1-го типоразмера. Из одной плиты по первому варианту раскроя получаются две таких заготовки, из 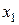плит 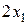заготовок 1-го типоразмера. Кроме того, по одной такой заготовке получится при раскрое каждой плиты по второму варианту. Всего по этому варианту раскраивается 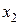плит, из которых вырабатывается, следовательно, 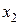заготовок 1-го типоразмера. По третьему варианту такие заготовки не получают. Значит, общее количество равно 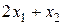. Поэтому имеем ограничение

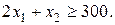(5.7)

Аналогичным образом составляется ограничение по выработке заготовок 2-го типоразмера

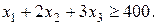(5.8)

Выражение для суммарного количества отходов при раскрое является минимизируемой целевой функцией и имеет вид

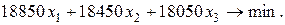(5.9)

Наконец, следует учесть естественные ограничения на неотрицательность переменных

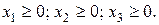(5.10)

Совокупность соотношений (5.7)... (5.10) представляет собой математическую модель данной задачи, которая, как и в предыдущем случае, является примером ЗЛП.

Задача о рациональном использовании сырья. Имеется сырье 1-го и 2-го сорта в количестве соответственно 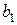и 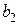м³. Три предприятия по его переработке, выпускающие однородную продукцию, располагают свободными мощностями, позволяющими переработать соответственно 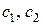и 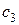м³ сырья. Эти предприятия работают в разных условиях и имеют соответственно различные нормы выхода продукции. Пусть 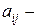объем продукции, вырабатываемой из 1 м³ сырья 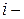го сорта на 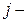м предприятии,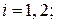 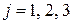. Требуется определить, в каком количестве необходимо поставлять сырье каждого сорта на каждое из предприятий. При этом должен быть обеспечен максимальный объем выпуска продукции и учтены ограничения по запасам сырья и объемам его переработки на предприятиях. Элементы решения в данной задаче удобно обозначить переменными с двумя индексами: первый индекс – сорт сырья, второй – номер предприятия. Таким образом, через 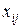обозначен объем сырья 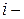го сорта, поставляемого на 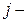е предприятие. Задача поэтому содержит шесть элементов решения: 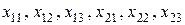. Общий объем сырья 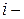го сорта, поставляемого на все три предприятия, равен сумме 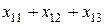и не должен превышать имеющегося запаса 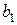м³. Следовательно, имеем группу из двух ограничений по запасам сырья каждого сорта:

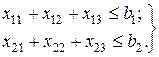(5.11)

Объем поставок сырья 1-го и 2-го сорта на первое предприятие, равный 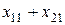, не должен превышать мощность 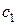этого предприятия по его переработке. Исходя из этого составляются ограничения по мощности переработки сырья для первого и остальных предприятий:

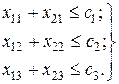(5.12)

Общий объем выработки продукции на всех предприятиях равен сумме

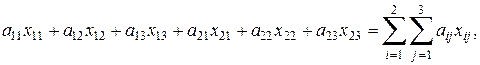
для которой надо найти максимум. Это выражение служит целевой функцией задачи:

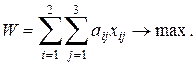(5.13)

Кроме того, надо учесть требование неотрицательности переменных:

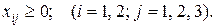(5.14)

Построенная математическая модель (5.11)... (5.14) – это еще один пример ЗЛП.

Общая постановка задачи линейного программирования. Сформулируем задачу линейного программирования в общем виде. Имеется 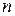переменных 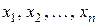. Требуется найти такие их значения, при которых целевая функция 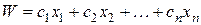(5.15) обращается в максимум (минимум). При этом переменные 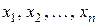должны удовлетворять ряду ограничений, каждое из которых должно относиться к одному из следующих типов:

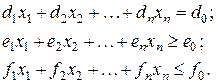(5.16 – 5.18)

Кроме того, имеются ограничения вида

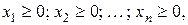(5.19)

которые называют обычно простыми или тривиальными ограничениями. Очевидно, что ограничения вида (5.18) легко сводятся к виду (5.17) умножением обеих частей исходного неравенства на (-1) и обратно – вид (5.17) к виду (5.18). От ограничений-равенств (5.16) тоже всегда можно перейти к эквивалентному неравенству вида (5.17) посредством исключения какой-либо переменной.

Запишем задачу линейного программирования общего вида в следующей форме:

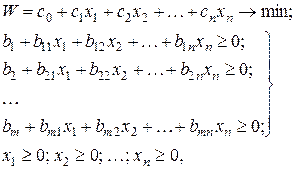(5.20 – 5.23)

где 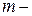число нетривиальных ограничений.

Совокупность значений переменных 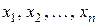, удовлетворяющая всем ограничениям ЗЛП, называется ее допустимым решением. Оптимальным решением ЗЛП называется такое ее допустимое решение, при котором целевая функция достигает экстремума, т. е. максимума или минимума, в зависимости от условий задачи.

Дата добавления: 2014-01-07