
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матричная форма уравнений контурных токов
Одним из возможных способов снижения порядка решаемой системы уравнений является использование контурных уравнений состояния.
Запишем II закон Кирхгофа в матричной форме
N ZBI = ЕК
Выразим матрицу токов в ветвях I через вектор контурных токов IК, используя следующие известные уравнения связи между ними
I = Nt IК (1.13)
Подставим выражение (1.13) в уравнение II закона Кирхгофа
N ZB Nt IК = ЕК
Произведение трех матриц N ZB Nt позволяет получить матррицу контурных сопротивлений
ZК = N ZB Nt (1.14)
Тогда матричное уравнение контурных токов можно записать в виде:
ZК IК = ЕК (1.15)
Структура:
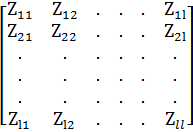 .
.  =
= 
l – количество независимых контуров расчетной схемы.
Структура матрицы ZB определяется физическим смыслом ее элементов, а именно:
-на главной диагонали расположены Zii – собственные сопротивления контуров i, равные сумме сопротивлений ветвей, входящих в контур;
-симметрично относительно главной диагонали расположены взаимные сопротивления контуров Zij = Zji, равные сумме сопротивлений ветвей, общих для контуров i и j.
Уравнения контурных токов применяются при расчете установившихся режимов, если моделирование нагрузки и генерации осуществляется с помощью источников ЭДС и задающих токов Ji = 0.
Матрица контурных сопротивлений ZК не является слабозаполненной, поэтому требуется больше оперативной памяти при реализации алгоритма расчета режим на ЭВМ.
Пример 1.7

Составить уравнение контурных токов в матричной форме и перейти к системе уравнений.
Z1 = 0,1 Е1 = 100
Z2 = 0,3 Е3 = 300
Z3 = 0,5 Е4 = 600
Z4 = 0,6
Z5 = 0,7
1.Составим матрицу инциденций второго рода
1 2 3 4 5
N = 
2.Произведем транспонирование матрицы N
Nt = 
3.Определим матрицу контурных сопротивлений по (1.14)и матрицу контурных ЭДС
ZК=  .
.  .
.  =
=
= .
.  =
= 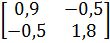
EК = N ZB =  .
.  =
=  =
= 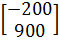
4.Запишем матричной уравнение контурных токов (1.15) и перейдем к системе уравнений
ZК IК = ЕК
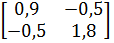 .
. 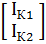 =
= 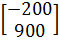
 0,9
0,9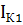 - 0,5
- 0,5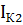 = -200
= -200
-0,5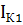 +1,8
+1,8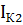 = 900
= 900
Порядок расчета установившегося режима при такой форме уравнений состояния сводится к следующему:
1.решается система уравнений (1.15) и определяются контурные токи 
2.по уравнению связи параметров [1] рассчитываются ток в ветвях схемы
I = Nt IК
3.по закону Ома (1.1) находятся падения напряжения в ветвях
UB = ZBI - EB
4.по уравнению связи [1] определяются узловые напряжения
UΔ = Мt-1 UB
5.далее могут быть рассчитаны все требуемые параметры режима P, Q, ΔP, ΔQ и т.д.
Таким образом, использование уравнений контурных токов уменьшается порядок решаемой системы уравнений до l, но увеличивается количество этапов расчета.
Задание 5.
Предположив наличие ЭДС в ветвях 2,5 расчетной схемы ЕВ2 = 100, ЕВ5 = 300, записать уравнение контурных токов в матричной форме и в виде системы уравнений.
Математические задачи в электроэнергетике.
Основы расчетов установившихся режимов в ЭЭС.
Постановка задачи расчетов.
1. Определяется особенностями ЭЭС.
2. Включает в себя большое количество элементов.
3. Элементы ЭЭС вырабатывают, преобразуют, распределяют, потребляют эл. энергию.
4. Элементы ЭЭС образуют сложнозамкнутую разветвленную структуру.
Факторы, обуславливающие функционирование ЭЭС:
1. Непрерывность процесса производства, распределения, потребления ЭЭ.
2. Динамизм ЭЭС (постоянное изменение тех. параметров).
3. Сложность структурных связей.
Режим работы ЭЭС- состояние системы в любой момент времени(либо на интервале времени).
Установившийся режим- режим работы ЭЭС, при котором её параметры на рассматриваемом интервале времени сохраняются неизменными или изменяются медленно.
Задачи расчета установившихся режимов:
Определение совокупности параметров: напряжений в различных точках системы. токов в элементах системы, потоков энергии между элементами и потерь мощности.
Этапы расчета:
1. Предварительное преобразование и переход к расчетной схеме ЭЭС.
2. Формирование уравнений состояния по известным исходным данным.
3. Выбор метода расчета, составление алгоритма и программы.
4. Проведение расчета установившегося режима.
5. Анализ точности полученных результатов.
Формирование расчетной схемы.
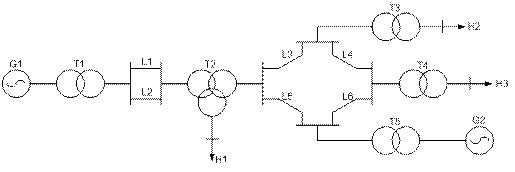
Схема замещения ЭЭС- совокупность схем замещения отдельных элементов системы, соединенных в той же последовательности, что и в реальной схеме.
Электрическая принципиальная схема ЭЭС включает 3 группы элементов: генераторы, потребители. электрические сети.
В схеме замещения генераторы обозначаются источниками тока либо напряжения. Потребители могут обозначаться как эл. сопротивление, либо как источник тока с отрицательным током.

Для упрощения схема приводится к одному напряжению, и объединяются сопротивления трансформаторов либо с источниками питания, либо с нагрузками.
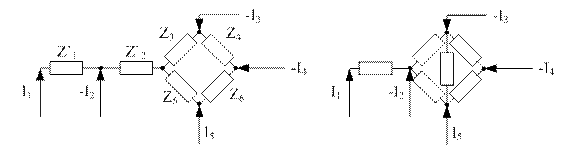
По полученной схеме составляется направленный граф. Граф содержит ту же информацию, что и схема уравнений, по которой он оставлен. Узлами графа могут являться токи ветвей (1-ый закон Кирхгофа) или Напряжения элементов (2-ой закон Кирхгофа), потенциалы узловых точек схемы (закон Ома).
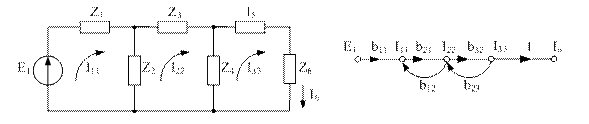
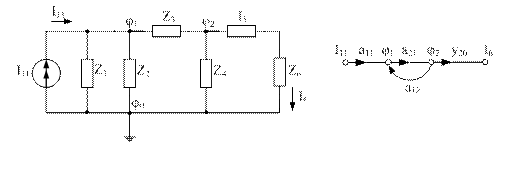
Составление графа на основе метода контурных токов.
Узлами графа являются уравнения контурных токов всех контуров схемы плюс входные величины - ЭДС, плюс входная величина. Все величины, входящие в уравнения контурного тока  соединяются с узлом передачи, направленной к узлу
соединяются с узлом передачи, направленной к узлу  . Узлы
. Узлы  могут иметь прямые и обратные передачи, узлы
могут иметь прямые и обратные передачи, узлы  – только прямые (выходящие), выходная величина- входящие.
– только прямые (выходящие), выходная величина- входящие.
Каждый узел  соединен с узлом
соединен с узлом  передачей
передачей 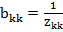 , где
, где  - суммарное соединение k-го контура.
- суммарное соединение k-го контура.
При этом величина  имеет знак «+», если напряжение ЭДС совпадает с направлением контурного тока
имеет знак «+», если напряжение ЭДС совпадает с направлением контурного тока  .
.
Каждый узел  соединен с узлом
соединен с узлом 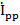 , если у контуров k и p есть общая ветвь, передачей
, если у контуров k и p есть общая ветвь, передачей  , где
, где  – сопротивление смежной ветви между k-ым и p-ым контурами.
– сопротивление смежной ветви между k-ым и p-ым контурами.
При этом 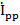 соединен с
соединен с  передачей
передачей 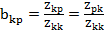 .
.
 ;
;  ;
;  ;
; 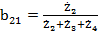 ;
; 
Составление графов на основе метода узловых потенциалов.
Узлами графа являются узловые потенциалы, узловые токи(втекающие в узел)- входные величины, и выходные величины. Если в схеме имеется источник ЭДС с сопротивлением, его заменяют эквивалентным источником тока.
Если на схеме узлы k и p соединены ветвью с проводимостью 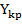 , и суммарная проводимость ветвей, сходящихся в узлах k и p, равна соответственно
, и суммарная проводимость ветвей, сходящихся в узлах k и p, равна соответственно 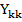 и
и 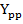 , то на графе между узлами
, то на графе между узлами 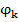 и
и  имеются 2 ветви. Передача той, что направлена к
имеются 2 ветви. Передача той, что направлена к 
 . Узел
. Узел 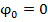 как бы не существует. Узел
как бы не существует. Узел 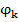 соединен с узлом узлового тока
соединен с узлом узлового тока  передачей
передачей  (к узлу k).
(к узлу k).
 ;
;  ;
; 
Обобщенная формула передачи направленного графа.
Прямой путь P- путь вдоль стрелок от истока к стоку, при прохождении которого ни один из узлов не встречается более одного раза.
Передача прямого пути равна произведению передач ветвей этого пути.
Второй (третий и т.д.) прямой путь - альтернативный путь.
Петля обратной связи - замкнутый путь, вдоль которого каждый узел может встретиться только один раз.
Передача петли обратной связи Т равна произведению передач ветвей, образующих эту петлю.
Обобщенная формула передачи графа (формула Мэзона).

 – передача прямого k-ого пути; n- число прямых путей;
– передача прямого k-ого пути; n- число прямых путей;
 -определитель прямого k-ого пути- равен единице минус сумма взятых поодиночке петель обратной связи грифа, не касающихся k-ого прямого пути, плюс сумма по парных произведений передач петель обратных связей, не касающихся друг друга и k-ого прямого пути, минус сумма тройных произведений петель обратных связей, не касающихся друг друга и k-ого прямого пути, плюс…
-определитель прямого k-ого пути- равен единице минус сумма взятых поодиночке петель обратной связи грифа, не касающихся k-ого прямого пути, плюс сумма по парных произведений передач петель обратных связей, не касающихся друг друга и k-ого прямого пути, минус сумма тройных произведений петель обратных связей, не касающихся друг друга и k-ого прямого пути, плюс…
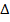 -определитель графа- равен единице минус сумма взятых поодиночке петель обратных связей, не касающихся друг друга, минус сумма тройных произведений передач петель обратной связи, не касающихся друг друга, плюс…
-определитель графа- равен единице минус сумма взятых поодиночке петель обратных связей, не касающихся друг друга, минус сумма тройных произведений передач петель обратной связи, не касающихся друг друга, плюс…

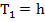
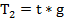
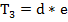
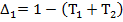

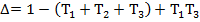

Матричная форма представления основных законов электротехники.
1. Закон Ома для участка цепи.

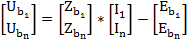
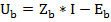
2. Первый закон Кирхгофа 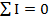
J=M*I
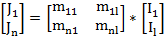
3. Второй закон Кирхгофа
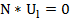
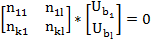
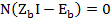
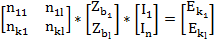

Матричная форма уравнений состояния электросистемы.
Матричное уравнение состояния электросистемы- система уравнений, описывающая режим работы электросистемы.
Виды матричных уравнений состояния:
1. Обобщенное уравнение состояния.
2. Уравнение узловых напряжений.
3. Уравнение контурных токов.
Обобщенное уравнение состояния получается за счет объединения уравнений состояния, составленных по 1-му и 2-му законам Кирхгофа.



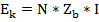
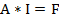 – обобщенное уравнение.
– обобщенное уравнение.
Матричная форма представления уравнения узловых напряжений.
Ток ветвей из 1-ого закона Ома 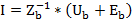
Из 1-ого закона Кирхгофа 
 ;
; 
Обозначим 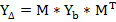 - матрица узловых проводимостей.
- матрица узловых проводимостей.
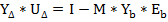
Физический смысл матрицы узловых проводимостей следующий:
На главной диагонали расположены элементы 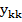 - сумма проводимостей всех ветвей, сходящихся в узел k. Прочие элементы
- сумма проводимостей всех ветвей, сходящихся в узел k. Прочие элементы  – взаимные проводимости ветвей между I и j, взятые с противоположным знаком.
– взаимные проводимости ветвей между I и j, взятые с противоположным знаком.
Этапы расчета по методу узловых напряжений.
1. Определяются значения узловых напряжений
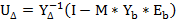
2. Определяются падения напряжений в ветвях
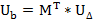
3. Определяются токи ветвей из закона Ома

4. Рассчитываются остальные параметры режима.
Матричная форма представления уравнений контурных токов.
Ток ветвей из 2-ого закона Кирхгофа 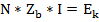
Обозначим  – матрица контурных токов.
– матрица контурных токов.
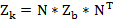 - матрица контурных сопротивлений.
- матрица контурных сопротивлений.

Физический смысл матрицы контурных токов следующий:
На главной диагонали расположены элементы  – сумма сопротивлении контура k. Прочие элементы
– сумма сопротивлении контура k. Прочие элементы  - сумма сопротивлений, смежных контуром I и j.
- сумма сопротивлений, смежных контуром I и j.
При наличии задающих токов в схеме равнения контурных токов имеют вид
 ,
,
 - матрица распределений задающих токов в ветвях.
- матрица распределений задающих токов в ветвях.
Для получения  необходимо из исходного графа сделать дерево, убрав из каждого контура по одной ветви. В результате матрица M станет квадратной.
необходимо из исходного графа сделать дерево, убрав из каждого контура по одной ветви. В результате матрица M станет квадратной.
 . Матрица
. Матрица  имеет (b-k) строк, где b- число ветвей, k- число вычеркнутых ветвей.
имеет (b-k) строк, где b- число ветвей, k- число вычеркнутых ветвей.
Матрица  получается из матрицы
получается из матрицы  возвращением соответствующих вычеркнутых строк на их место. Элементы этих строк равны нулю.
возвращением соответствующих вычеркнутых строк на их место. Элементы этих строк равны нулю.
Методы исследования статической устойчивости электроэнергетических систем.
Постановка задачи расчетов:
Задача исследования устойчивости ЭЭС требует наличия методов, которые давали бы возможность по доступным, легко полученным признакам, устанавливать устойчивость системы.
Критерий устойчивости- необходимое и/ или достаточное условие (группа условий), при выполнении которых система является устойчивой.
Основной критерий устойчивости состояния системы
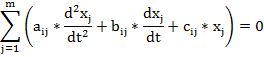
Характеристическое уравнение имеет вид
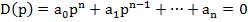
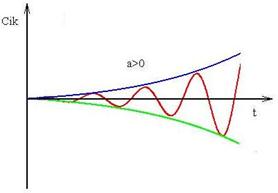
Равенство нулю характеристического уравнения возможно, только если все его корни имеют отрицательные вещественные части.
Для того, чтобы состояние равновесия было устойчивым, необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой комплексной полуплоскости.
Характеристическое уравнение, как правило, имеет несколько действительных и несколько комплексно-сопряженных корней. При простых корнях общее решение системы имеет вид
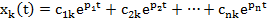 , c= const,
, c= const, 

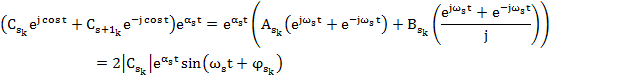
 ;
; 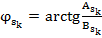




Алгебраический критерий устойчивости.
Содержит группу условий - неравенств, при соблюдении которых система устойчива.
Для проведения алгебраического анализа необходимы коэффициенты характеристического уравнения.
1. Если все коэффициенты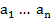 положительны, состояние системы устойчиво.
положительны, состояние системы устойчиво.
2. Если при изменении параметров системы хотя бы один из коэффициентов меняет знак, система неустойчива.
3. Необходимые условия устойчивости представляют собой различные соотношения.
1. Критерий Гурвица.
Устанавливает соотношения в форме неравенств, соблюдение которых является необходимым и достаточным условием устойчивости системы.

Матрица Гурвица

Все коэффициенты с индексом i<0 или i>n обозначаются нулями.
Для соблюдения устойчивости требуется, чтоб все n диагональных миноров матрицы Гурвица были положительны.


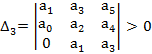 …
… 
Критерий Гурвица используется для определения устойчивости систем 3-4-го порядков.
2. Критерий Рауса.
Используется для систем порядка выше 4, когда параметры заданы числами.
Из коэффициентов характеристического уравнения составляется таблица Рауса с количеством строк n+1.
Элементы 1-й строки- коэффициенты с четными индексами.
Элементы 2-й строки- коэффициенты с нечетными индексами.
Элементы следующих строк находятся по формуле
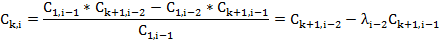

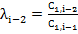 ; I ≥ 3, k- номер столбца, i-номер строки.
; I ≥ 3, k- номер столбца, i-номер строки.
Необходимое и достаточное условие устойчивости:
Все коэффициенты первого столбца должны быть положительны
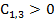 ,
, 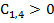 ,
,  …
… 
Число перемен знаков в 1-м столбце таблицы Рауса равно числу корней характеристического уравнения.
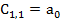

| 

| 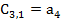

| 

| |

| 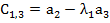
| 
| 
| 
|
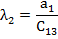
| 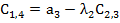
| 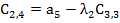
| 
| 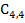
|
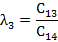
| 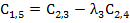
| 
| 
| 
|
Если числа в 1-м столбце отличны от нуля, таблица называется регулярной. В регулярном случае характеристическое уравнение не имеет чисто мнимых корней.
Если в 1-м столбце есть нулевой элемент, таблица называется нерегулярной. В этом случае для построения таблицы строку, в которой элементы  , заменяют следующей строкой
, заменяют следующей строкой

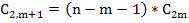

ПРИМЕР.
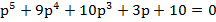
 ;
; 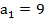 ;
; 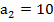 ;
;  ;
; 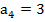 ;
; 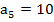
 1 1
 9 9
|  10 10
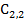 0 0
| 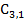 3 3
 10 10
| 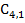 0 0
 0 0
| |
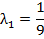
|  10 10
|  17/9 17/9
| 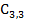 0 0
|  0 0
|
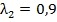
|  -1,7 -1,7
| 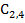 10 10
|  0 0
| 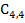 0 0
|
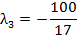
| 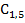 17/9+1000/17 17/9+1000/17
| 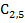 0 0
|  0 0
|  0 0
|

|  10 10
| 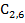 0 0
|
Вывод: система неустойчива.
3. Критерий Михайлова.
Принцип аргумента:
Разность между числом нулей и числом полюсов функции F(p) внутри контура С равен числу оборотов, которое делает вектор в плоскости W(jω), идущий из O в F(p), когда точка p описывает контур С.
Критерий Михайлова:
Для отсутствия корней с положительной действительной частью характеристического уравнения (т.е. для обеспечении устойчивости), необходимо и достаточно, чтобы при прохождении точкой p мнимой оси в положительном направлении приращение аргумента D(p) было равно n.П.
Характеристическое уравнение представим в виде

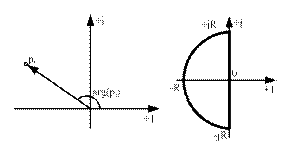
p представляет собой вектор в комплексной плоскости, длина которого равна модулю p, а угол, образованный с вещественной осью равен аргументу p.
Возьмем в качестве контура С полуокружность радиуса R с центром в начале координат. Положительный обход контура: -jR→ 0→ jR→ -R→-jR (против часовой стрелки от точки (0; -jR)).
Поскольку функция D(p) не имеет полюсов, то, согласно принципу аргумента, число оборотов, которые совершит вектор функции D(p) при обходе вектором p контура С, равно числу корней уравнения  , лежащих внутри С и на нем самом.
, лежащих внутри С и на нем самом.
При  все корни с отрицательной вещественной частью, окажутся внутри С. Согласно принципу аргумента, их число равно
все корни с отрицательной вещественной частью, окажутся внутри С. Согласно принципу аргумента, их число равно  , где
, где  - приращение, полученное аргументом вектора
- приращение, полученное аргументом вектора  при обходе вектором p контура С.
при обходе вектором p контура С.
Модуль вектора 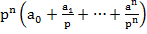 равен произведению модулей p и
равен произведению модулей p и  , а аргумент этого вектора равен сумме их аргументов.
, а аргумент этого вектора равен сумме их аргументов.
Т.о. 
При изменении аргумента p на π аргумент  изменится на p*π, т.е.
изменится на p*π, т.е.  . При
. При  вектор
вектор 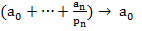 при
при 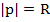 . Т.о. его приращение
. Т.о. его приращение 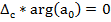
При движении вектора p по мнимой оси от –jR до jR, т.е. от -j∞ до +j∞ 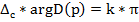 , где
, где 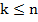
Т.о. число корней характеристического уравнения, лежащих в левой полуплоскости, равно n/2, а число чисто мнимых корней равно k/2. Если k=n, то число корней, охватываемых контуром С равно n, т.е. все корни имеют неположительную действительную часть, что соответствует устойчивости системы.
Для определения устойчивости по Михайлову необходимо определить приращение аргумента 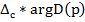 при перемещении вектора p только по мнимой оси. Представим уравнение в виде
при перемещении вектора p только по мнимой оси. Представим уравнение в виде
 , где
, где  - корни характеристического уравнения.
- корни характеристического уравнения.
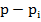 - так же векторы на комплексной плоскости, модуль и аргумент которых зависит от p.
- так же векторы на комплексной плоскости, модуль и аргумент которых зависит от p.
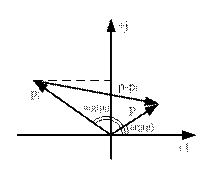
Направим вектор p по мнимой оси, т.е. примем 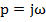 . Тогда конец вектора
. Тогда конец вектора  будет направлен по мнимой оси. При изменении ω от -∞ до +∞ (т.е. при перемещении p по мнимой оси) вектор
будет направлен по мнимой оси. При изменении ω от -∞ до +∞ (т.е. при перемещении p по мнимой оси) вектор  получит приращение угла от
получит приращение угла от 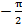 до
до 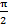 , т.е.
, т.е. 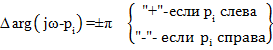
Поскольку  , то
, то 
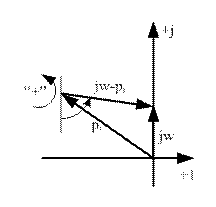
Если все корни характеристического уравнения лежат в левой полуплоскости, то  .
.
Если m корней лежат в правой полуплоскости, то 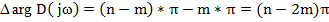

Вектор 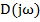 называется характеристическим вектором.
называется характеристическим вектором.
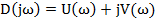
Характеристический вектор, изображенный в декартовых координатах U и V при изменении  от -∞ до +∞ описывает своим концом кривую, называемую характеристической кривой или годографом характеристического уравнения.
от -∞ до +∞ описывает своим концом кривую, называемую характеристической кривой или годографом характеристического уравнения.

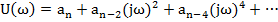

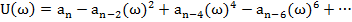

 ;
; 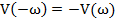 . Т.о. годограф симметричен относительно действительной оси.
. Т.о. годограф симметричен относительно действительной оси.

Это позволяет сформулировать критерий Михайлова в следующем виде:
Система устойчива, если 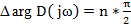 ;
; 
Система неустойчива, если  ;
; 
Для обеспечения устойчивости необходимо и достаточно:
1. 
2. 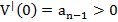
3. Все корни уравнений  и
и  - действительные и перемежающиеся, т.е. между двумя соседними корнями уравнения
- действительные и перемежающиеся, т.е. между двумя соседними корнями уравнения  лежит корень
лежит корень 

Пример 1.
Определить устойчивость системы с характеристическим многочленом вида:

Решение.
Воспользуемся критерием Михайлова
 ;
; ;
;  ;
; 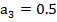
Характеристический вектор:




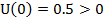 ;
; 
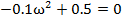 ;
; 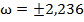
 ;
;  ,
, 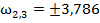
Корни уравнений  и
и  действительные и перемежающиеся
действительные и перемежающиеся
| ω | U | V |
| 0.5 | ||
| 2.236 | 2.504 | |
| 3.786 | -0.933 | |
| ∞ | -∞ | -∞ |
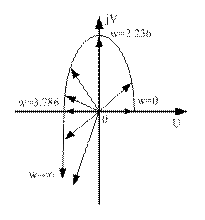
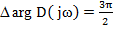
n=3
Вывод: система устойчива.
СТРАНИЦА 18
4. Критерий Найквиста.
При изучении устойчивости и качества переходных процессов в технических системах необходимо исследовать математическую модель- систему диф. уравнений, описывающих переходные процессы. Основой для их получения служит представление системы в виде структурной схемы, состоящей из звеньев и связей между ними. Для анализа диф. уравнений удобно использовать метод преобразований Лапласа, где исследуемые функции заменяют их изображениями X(t)→X(p), в результате чего система диф. уравнений преобразуется в систему алгебраических уравнений.
Этот прием используется также для анализа взаимосвязей элементов (звеньев)системы.
Передаточная функция  звена- отношение к изображению
звена- отношение к изображению  переменной, поданной на вход звена, изображений переменной
переменной, поданной на вход звена, изображений переменной 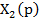 , полученной на его выходе.
, полученной на его выходе.


Зная Структурную схему и передаточную функцию каждого звена системы, можно получить передаточную функцию всей системы.
1. При последовательном соединении звеньев.
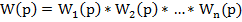

2. При параллельном соединении звеньев
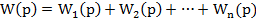

3. Передаточная функция разомкнутой системы, содержащей последовательно и параллельно соединенные звенья, может быть представлена в виде
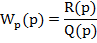
где 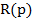 и
и 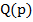 - многочлен, причем
- многочлен, причем 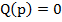 - характеристическое уравнение системы.
- характеристическое уравнение системы.
Разомкнутую систему можно превратить в замкнутую (саморегулируемую) введением обратной связи.

Если Wp (P)-передаточная функция разомкнутой системы, Wос(p)-передаточная функция звена обратной связи, то передаточная функция замкнутой системы
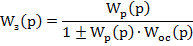
 Где «-» соответствует положительной, а «+» -отрицательной ОС.
Где «-» соответствует положительной, а «+» -отрицательной ОС.
В случае, когда Wос(p)=1
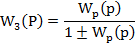
Поскольку  ,
, 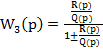
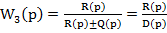
 Т.е. D(p)=Q(p)±R(p)- характеристический многочлен замкнутой системы с одиночной ОС.
Т.е. D(p)=Q(p)±R(p)- характеристический многочлен замкнутой системы с одиночной ОС.
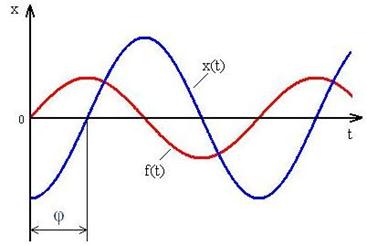
Если на вход линейно устойчивой системы длительно действует, гармоничны изменяющиеся силы 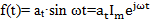 , то после затухания переходных процессов на выходе установятся гармоничные колебания x(t) c той же частотой, одного с другими амплитудой и начальной функцией, определяемыми параметрами систем.
, то после затухания переходных процессов на выходе установятся гармоничные колебания x(t) c той же частотой, одного с другими амплитудой и начальной функцией, определяемыми параметрами систем.
Уравнение, связывающее входные и выходные величины

Поскольку 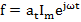 ;
; 

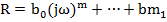

Передаточная функция W(Р) при Р=j называется комплексным коэффициентом усиления системы
называется комплексным коэффициентом усиления системы 
Модуль вектора 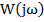 называет, во столько раз амплитуда выходных колебаний больше амплитуды входных, аргумент- разность фаз между этими колебаниями.
называет, во столько раз амплитуда выходных колебаний больше амплитуды входных, аргумент- разность фаз между этими колебаниями.
Зависимость А( ),
),  , W(
, W( )называются соответственно амплитудно -частотной, фазово-частотной и амплитудно - фазовой характеристиками системы (АЧХ;ФЧХ;АФХ)
)называются соответственно амплитудно -частотной, фазово-частотной и амплитудно - фазовой характеристиками системы (АЧХ;ФЧХ;АФХ)
Для анализа устойчивости системы, ряд звеньев которой задан лишь амплитудно-фазовыми характеристиками, применяют критерий Найквиста.
Критерий Найквиста основан на применении принципа аргумента к вектору - годографу комплексного коэффициента усиления разомкнутой системы.
Он позволяет по АФХ разомкнутой системы определить устойчивость соответствующей замкнутой системы.
Пусть  предаточна функция разомкнутой системы.
предаточна функция разомкнутой системы. 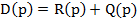 . Рассмотрим функцию
. Рассмотрим функцию . Приращение аргумента данного вектора при
. Приращение аргумента данного вектора при 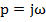 ;
;
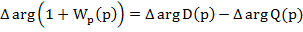 .
. 
Т.е. приращение аргумента вектора  равно разности приращений аргументов характеристических векторов замкнутой и разомкнутой системы. Согласно критерию Михайлова, для устойчивости замкнутой системы
равно разности приращений аргументов характеристических векторов замкнутой и разомкнутой системы. Согласно критерию Михайлова, для устойчивости замкнутой системы 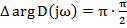 .
.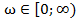 Для разомкнутой системы
Для разомкнутой системы  определяется её состоянием и числом m корней в правой полуплоскости. Если система устойчива,
определяется её состоянием и числом m корней в правой полуплоскости. Если система устойчива,  , если нет-
, если нет-  .
.
Необходимое и достаточное условие устойчивости замкнутой системы:
1. Для устойчивой разомкнутой системы 
2. Для неустойчивой разомкнутой системы 
Возможная формула АФХ разомкнутой системы определяются рядом условий:
1. Если многочлен Q(p)и R(p) имеют положительные свободные члены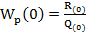 , т.е. АФХ начинается на положительной полуоси (рис. а, б, в, д, е)
, т.е. АФХ начинается на положительной полуоси (рис. а, б, в, д, е)
2. Если многочлен Q(p)имеет нулевой корень, т.е. разомкнутся система находится на границе апериодической устойчивости (нейтральна),  , и АФХ при ω→0 уходит в бесконечность в сторону –j (рис 2.)
, и АФХ при ω→0 уходит в бесконечность в сторону –j (рис 2.)
3. Если Q(p)имеет пару чисто мнимых корней. т.е. разомкнутая система находится на границе периодической устойчивости(нейтральна)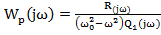 , и АФХ имеет разрыв в точке p=jωo. (рис. д.)
, и АФХ имеет разрыв в точке p=jωo. (рис. д.)
4. Если степень R(p) меньше, чем Q(p),  (рис. А - д).
(рис. А - д).
Если степени R(p)и Q(p)равны,  (рис. е)
(рис. е)
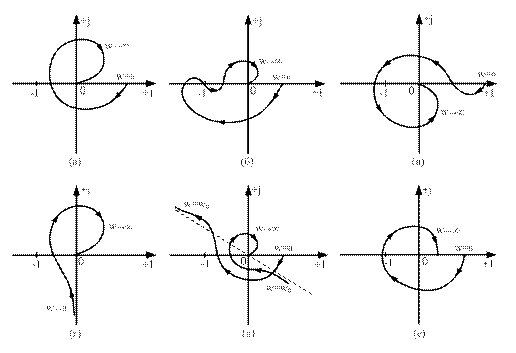
Вектор 1+ имеет начало b т.е. (-1;0) и конец b точке - конец вектора
имеет начало b т.е. (-1;0) и конец b точке - конец вектора  . Если
. Если  , то АФХ разомкнутой системы не охватывает точку С. Если
, то АФХ разомкнутой системы не охватывает точку С. Если 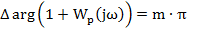 , то АФХ
, то АФХ  охватывает т. С
охватывает т. С  раз.
раз.
Геометрическая формулировка критерия Найквиста:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы:
1. АФХ устойчивой или нейтральной разомкнутой системы не охватывала точкуС(-1;0)

2. АФХ неустойчивой разомкнутой системы охватывала точку С(-1;0)  раз.В положительном направлении
раз.В положительном направлении
Если многочлен Q(jω) имеет высокую степень, то для построения АФХ разомкнутой системы требуется большие вычисления. В этом случае удобнее использовать инверсную амплитудно-фазовую характеристику
 .
.
Критерии Найквиста для ИАФХ:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы ИАФХ устойчивой разомкнутой системы охватывала точку С (-1;0)
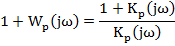
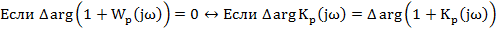
24 СТРАНИЦА
Пример 2.
Определить устойчивость замкнутой системы, есликомплексный коэффициент усиления устойчивой разомкнутой системы
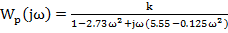
Где 
Решение:
Воспользуемся критерием Найквиста для ИАФХ.
При К=1  =-2,73ω2+1+jω(-0.125ω2+5.55)
=-2,73ω2+1+jω(-0.125ω2+5.55)
U(ω)= =-2,73ω2+1
jV(ω)= (-0.125ω2+5.55) jω
U(0)=1>0; V'(0)=5.55>0
-2,73ω2+1=0 ω(-0.125ω2+5.55)=0
ω=±0.605 ω1=0; ω2,3=±6,663
| ω | U | V |
| 0.605 | 3.33 | |
| 6.663 | -120.2 | |
| ∞ | -∞ | -∞ |
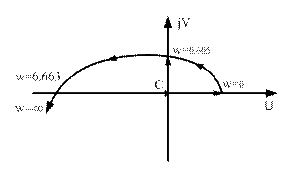
При К=1 ИАФХ охватывает точку С, т.е. система устойчива.
При уменьшении К  будет возрастать, т.е. ИАФХ получится преобразованием подобия из исходной с центром в начале координат (масштабированием).
будет возрастать, т.е. ИАФХ получится преобразованием подобия из исходной с центром в начале координат (масштабированием).
При увеличении К ИАФХ бк\удет сжиматься т.е. при К=120,2 ИАФХ будет проходить через точку С(-1;0), т.е. система будет находится на границе устойчивости.
При К>120,2ИАФХ не будет охватывать точку С и сестема будет неустойчивой.
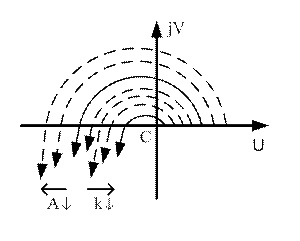
Выделение областей устойчивости.
В технических задачах часто важно знать, в каких пределах можно изменять те или иные параметры системы, не нарушая её устойчивости. Это определенным образом характеризует запасы устойчивости системы и надежность её работы, дает понятие о необходимой точности настройки автоматического регулятора. Целью исследования в этом случае является отыскание всех значений исследуемых параметров, при которых система устойчива.
При решении таких задач выделяют области устойчивости (метод Ю.И. Неймарка).
Рассмотрим характеристическое уравнение п -й степени:
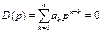
 При некоторых фиксированных значениях коэффициентов аk число т корней уравнения могут находиться в правой полуплоскости корней и (п – т) в левой. При плавном изменении коэффициентов аk корни уравнения в силу непрерывной зависимости от коэффициентов будут перемещаться на плоскости корней, образуя траектории корней.
При некоторых фиксированных значениях коэффициентов аk число т корней уравнения могут находиться в правой полуплоскости корней и (п – т) в левой. При плавном изменении коэффициентов аk корни уравнения в силу непрерывной зависимости от коэффициентов будут перемещаться на плоскости корней, образуя траектории корней.
Поясним это на примере уравнения третьей степени:
D(р) = а0р3 + а1р2 + а2р + а3 = 0.
 Пусть изображающая точка М в пространстве коэффициентов а1, а2, а3 перемещается из точки М1 в точку М2. В соответствии с этим корни характеристического уравнения перемещаются по траекториям корней от значений рiM1 к значениям рiM2. Совокупность коэффициентов аkN, при которых хотя бы один корень или пара комплексных корней находятся на мнимой оси, определяет собой поверхность N в пространстве коэффициентов. Если траектория точки М пересечет поверхность N, то траектория корней пересечет мнимую ось. Таким образом, поверхность N делит пространство коэффициентов аk на области D(m) c числом т корней в правой и (п – т) – в левой полуплоскости корней.
Пусть изображающая точка М в пространстве коэффициентов а1, а2, а3 перемещается из точки М1 в точку М2. В соответствии с этим корни характеристического уравнения перемещаются по траекториям корней от значений рiM1 к значениям рiM2. Совокупность коэффициентов аkN, при которых хотя бы один корень или пара комплексных корней находятся на мнимой оси, определяет собой поверхность N в пространстве коэффициентов. Если траектория точки М пересечет поверхность N, то траектория корней пересечет мнимую ось. Таким образом, поверхность N делит пространство коэффициентов аk на области D(m) c числом т корней в правой и (п – т) – в левой полуплоскости корней.
Такое разбиение пространства коэффициентов на области, соответствующие различному числу т корней в правой полуплоскости корней, называется D-разбиением, а поверхность N – границей D‑разбиения.
Граница D-разбиения в плоскости коэффициентов характеристического уравнения является отображением мнимой оси плоскости корней этого уравнения.
Обычно интерес представляют области D-разбиения и выделения устойчивости в пространстве каких-либо параметров системы, от которых в общем случае сложно зависят коэффициенты характеристического уравнения. В этом случае, зная связь между исследуемыми параметрами системы и коэффициентами характеристического уравнения и применяя способ, описанный ранее, можно найти границу D-разбиения в координатах этих параметров.
Алгоритм построения границы D-разбиения:
1) Выделить в характеристическом векторе действительную и мнимую части
D(jω) = U(ω) + jV(ω) = 0.
2) Записать систему уравнений
U(ω) = 0;
V(ω) = 0.
3) Для каждого значения ωk найденные коэффициенты системы будут определять точку на границе D-разбиения. Изменяя ω от –∞ до +∞ можно построить всю границу D-разбиения.
Пусть дана замкнутая система, характеристический многочлен которой имеет вид
D(р) = D0(p) + П1D1(р) + П2D2(р) + … + ПkDk(р),
где П1, П2,..., Пk, – выделенные параметры системы; D0(p), D1(р), …, Dk(р) – заданные полиномы.
Необходимо определить все значения П1, П2,..., Пk, при которых система устойчива, т. е. найти область устойчивости в пространстве параметров системы. В зависимости от числа выделенных параметров метод решения этой задачи называется методом D-разбиения по трем параметрам (k = 3), D‑разбиения по двум параметрам (k = 2), D‑разбиения по одному параметру (k = 1).
D‑разбиение по двум параметрам.
Будем рассматривать наиболее распространенный случай, когда два параметра входят в характеристический многочлен линейно (т. е. ни в одном из коэффициентов многочлена нет ни произведения, ни высших степеней П). Характеристическое уравнение системы
D(р) = D0(p) + П1D1(р) + П2D2(р) = 0.
Найдем значения П1 и П2, при которых характеристическое уравнение имеет пару чисто мнимых корней р1,2 =± jωi.
D(jω) = D0(jω) + П1D1(jω) + П2D2(jω) = 0
Уравнение распадается на два:
П2U2(ω) + П1U1(ω) = – U0(ω);
П2V2(ω) + П1V1(ω) = – V0(ω)
Решим систему с помощью правила Крамера:
 ;
;  ;
; 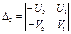 .
.
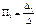 ;
; 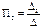 .
.
Кривые П1(ω), П2(ω) – четные функции, т.е. П(–ω) = П(ω). Определители Δ(ω), Δ1(ω), Δ2(ω) – нечетные функции. При изменении ω от –∞ до 0 получим кривую D‑разбиения на плоскости параметров П1 и П2. При изменении ω от 0 до +∞ получим ту же кривую, т.к. функции П(ω) – четные.
Особые прямые.
При изменении ω главный определитель Δ может менять знак. Прохождение значения Δ через нуль соответствует двум случаям:
1) при Δ = 0 значения Δ1 и Δ2 конечны и не равны нулю. Тогда П1 и П2 обращаются в бесконечность.
2) при Δ = 0 значение Δ1= Δ2 = 0. Тогда П1 и П2 становятся неопределенными. Равенство нулю определителей при фиксированном значении ωi означает, что все коэффициенты двух уравнений пропорциональны:

Тогда вместо двух уравнений можно записать одно:
П2U2(ωi) + П1U1(ωi) = – U0(ωi).
Это соотношение определяет в плоскости П2, П1 для некоторого фиксированного значения ω = ωi положение линии, называемой особой прямой. Чтобы найти особые прямые, надо определить все значения ωi, при которых одновременно Δ = Δ1= Δ2 = 0.
Для получения особых прямых нужно:
1) Приравнять а0 = 0, если оно зависит от П1, П2, и получить уравнение особой прямой, соответствующей ω = ∞;
2) Приравнять ап = 0, если оно зависит от П1, П2, и получить уравнение особой прямой, соответствующей ω = 0;
3) Найти все отличные от нуля значения ω, при которых Δ = Δ1= Δ2 = 0. Подставив эти значения ω в уравнение, получим уравнения соответствующих особых прямых.
Штриховка границ D-разбиения.
 Кривая D-разбиения и особые прямые разбивают плоскость П2, П1 на области с различным числом т корней в правой полуплоскости корней. Чтобы разметить разные области D(m) соответствующим индексом т, применяется правило штриховки.
Кривая D-разбиения и особые прямые разбивают плоскость П2, П1 на области с различным числом т корней в правой полуплоскости корней. Чтобы разметить разные области D(m) соответствующим индексом т, применяется правило штриховки.
Пусть изображающая точка М перемещается по плоскости П2, П1. До тех пор пока она перемещается внутри области D(m), и не попадает на кривую D-разбиения, число корней т в правой полуплоскости остается постоянным. Как только точка М попадает на кривую D-разбиения, на мнимую ось плоскости р выйдет пара корне й. При пересечении кривой D-разбиения эта пара корней перейдет из одной полуплоскости в другую. Чтобы выяснить направление перехода корней (из левой полуплоскости корней в правую или наоборот), применяется правило штриховки.

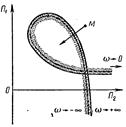 Сравним движение по мнимой оси плоскости корней с направлением движения по кривой D‑разбиения. Если в плоскости корней перемещаться по мнимой оси из – ∞ в + ∞, то область, где должны располагаться корни для того, чтобы система была устойчива, будет всегда слева. Заштрихуем слева мнимую ось jω. Перемещаясь вдоль границы D-разбиения из точки, соответствующей ω = –∞, к точке, соответствующей ω = +∞, заштрихуем кривую также слева в том случае, если Δ > 0. Изменение знака определителя меняет направление штриховки.
Сравним движение по мнимой оси плоскости корней с направлением движения по кривой D‑разбиения. Если в плоскости корней перемещаться по мнимой оси из – ∞ в + ∞, то область, где должны располагаться корни для того, чтобы система была устойчива, будет всегда слева. Заштрихуем слева мнимую ось jω. Перемещаясь вдоль границы D-разбиения из точки, соответствующей ω = –∞, к точке, соответствующей ω = +∞, заштрихуем кривую также слева в том случае, если Δ > 0. Изменение знака определителя меняет направление штриховки.
Правило штриховки: при обходе в сторону возрастающих ω (от –∞ до +∞) кривая D‑разбиения штрихуется слева, если главный определитель Δ > 0, и справа, если &#
|
|
Дата добавления: 2014-01-06; Просмотров: 2949; Нарушение авторских прав?; Мы поможем в написании вашей работы!