Комплексный чертёж точки

Наибольшее применение на практике получил чертёж, составленный из двух или более связанных между собой ортогональных проекций изображаемой фигуры. Такой чертёж называется комплексным чертежом в ортогональных проекциях или комплексным чертежом.

Принцип образования чертежа состоит в том, что данная фигура проецируется ортогонально на 2 взаимно ^-е плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.

Одна из плоскостей проекций располагается горизонтально, обозначается П₁ и называется горизонтальной плоскостью проекций.

2-я плоскость располагается вертикально перед наблюдателем, обозначается П₂ – фронтальная плоскость проекций. Прямая пересечения плоскостей – ось проекций.

А₁ – горизонтальная проекция А₂ – фронтальная проекция

h_А – высота точки А

f_А – глубина т.А

Спроецируем ортогонально на плоскости проекций П₁ и П₂ какую-нибудь

точку А, тогда получим две её проекции: горизонтальную проекцию А₁ на плос­кости П₁ и фронтальную проекцию А₂ на плоскости П₂. Проецирующие прямые AA₁ и АА₂, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость A₁AA₂, перпендикулярную к обеим плоскостям проекций и к оси проекций X. Прямые A_хA₁ и А_хА₂, являющиеся проекциями проецирующей плоскости на плоскостях проекций П₁ и П₂, будут перпендикулярны к оси проекций X.

Обратно, каждая пара точек А₁ и А₂, соответственно принадлежащих плос­костям П₁ и П₂ и расположенных на перпендикулярах к оси X, восставленных из одной и той же точки А_х, определяют в пространстве единственную точку А. В са­мом деле, если провести через точку A₁ и А₂ перпендикуляры А₁А и А₂А соответ­ственно к плоскостям П₁ и П₂, то они, находясь в одной плоскости А₁А_хА₂, пере­секутся в некоторой точке А. Расстояние A₁А точки А от горизонтальной плоскос­ти проекций называется высотой h точки А, ее расстояние А₂А от фронтальной плоскости проекций – глубиной f точки А.

Чтобы получить плоский чертеж, совместим плоскость проекций П₁ с плос­костью П₂, вращая переднюю полуплоскость П₁ вокруг оси Х вниз. В результате получим комплексный чертеж точки А (рис. 4), состоящий из двух проекций А₁ и А₂ точки А, лежащих на одной прямой, перпендикулярной к оси X. Прямая А₁А₂, соединяющая две проекции точки, называется вертикальной линией связи.

Полученный комплексный чертеж будет обратимым, т.е. по нему можно вос­становить оригинал. В самом деле, рассматривая, например, фронтальную проек­цию А₂ точки А и имея на чертеже ее глубину f=А_хА₁, можно построить точку А. Для этого надо восстановить перпендикуляр к плоскости чертежа в его точке А₂ и от плоскости чертежа отложить глубину искомой точки, тогда конец перпендику­ляра определит положение точки А.

На практике часто бывает безразличным положение изображаемой фигуры относительно неподвижной системы плоскостей проекций, поэтому при образова­нии комплексного чертежа можно отказаться от фиксации плоскостей проекций и оси проекций не изображать. Основанием этому может служить отмеченное шестое свойство параллельной проекции не изменять проекции фигуры при параллельном переносе плоскости проекций.

Плоскости проекций П₁ и П₂ разбивают все пространство на четыре части, называемые квадрантами или четвертями. При этом условимся нумеровать квад­ранты в порядке, указанном на рис., и называть их I, II, III и IV квадрантами.

Рис. 5 Двухкартинный комплексный чертёж  

Если точка А лежит в I квадранте, то ее горизонтальная проекция A₁ будет принадлежать передней полуплоскости П₁, а фронтальная проекция А₂ - верхней полуплоскости П₂. При совмещении плоскостей проекций горизонтальная проек­ция A₁ точки А окажется расположенной ниже оси Х₁₂, а фронтальная проекция А₂ - выше оси Х₁₂ (рис. 5). В зависимости от положения точек в различных квад­рантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже (рис. 5), так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит точка.

Итак, комплексный чертеж, состоящий из двух ортогональных проекций (на­зываемый еще двухкартинным чертежом), является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. В качестве такой плос­кости проекций применяется плоскость, перпендикулярная к обеим основным плоскостям П₁ и П₂, которая называется профильной плоскостью проекций. Ее обозначают П₃. Три плоскости проекций П₁, П₂ и П₃ образуют систему трех взаимно перпендикулярных плоскостей (рис. 6). Ребра полученного трехгранника будем обозначать через X, У, Z.

Рис. 6

П3 – профильная плоскость проекций А3 – профильная проекция т.А рА – широта т.А

трёхкартинный комплексный чертёж т.А

Рассмотрим построение трехкартинного комплексного чертежа. Пусть А - некоторая точка пространства. Опустим из точки А перпендикуляры на плоскости проекций П₁, П₂ и П₃: АА_i^П_i (i = 1, 2, 3). Основания этих перпендикуляров (точ­ки А₁, А₂, А₃) и являются соответственно горизонтальной, фронтальной и про­фильной проекциями точки А в системе плоскостей проекций П₁, П₂ и П₃. Заметим при этом, что проецирующие плоскости AA₁A₂, AA₁A₃ и АА₂А₃ перпендикулярны соответственно осям X, У, Z. Обозначив точки пересечения этих плоскостей с осями через А₁₂, А₁₃, А₂₃, заметим, что как прямые A₁A₁₂ и А₁₂А₂ перпендикулярны к оси X, так и две другие пары прямых A₁A₁₃, А₁₃А₃ и А₂А₂₃, А₂₃А₃ должны быть перпендикулярны соответственно осям Y и Z. Расстояние точки А от горизонтальной плоскости проекций П₁ мы назвали ранее высотой точки А, а расстояние точки А от фронтальной плоскости проекций П₂ - ее глубиной; расстояние точки А от профильной плоскости проекций П₃ будем называть широтой точки А.

При построении плоского чертежа плоскость П₂ считается неподвижной, а остальные плоскости П₁ и П₃ совмещаются с ней путем вращения соответственно вокруг осей Х и Z в направлении, указанном на рис. стрелками. После совме­щения плоскости П₁ с фронтальной плоскостью П₂ отрезки А₁А₁₂^Х₁₂ и A₁₂A₂^X₁₂ окажутся расположенными на одной прямой. Аналогично после со­вмещения плоскости П₃ с плоскостью П₂ отрезки A₂A₂₃^Z₂₃ и А₂₃А₃^Z₂₃ распо­ложатся на линии связи А₂А₃^Z₂₃.

В результате указанного совмещения плоскостей проекций получаем комп­лексный чертеж точки А, состоящий из трех ортогональных проекций (трехкартинный). При этом линии связи должны быть перпендикулярны к осям: А₁А₂^Х₁₂, А₂А₃^Z₂₃, а отрезки А₁А₁₂ и А₂₃А₃ равны, ибо А₁А₁₂ = А₂₃А₃ =А₂А есть глубина точки А.

Рассмотрим, какой линией связи можно соединять горизонтальную и про­фильную проекции точки А. Для этого обратим внимание на квадрат А₁₃ОА₃А*. Диагональ этого квадрата является биссектрисой угла Х₁₂ОZ₂₃. Следо­вательно, линия связи, соединяющая проекции А₁ и А₃, представляет собой лома­ную линию с вершиной на биссектрисе угла Х₁₂ОZ_23, состоящую из двух звеньев (горизонтального и вертикального). В дальнейшем эту линию будем называть горизонтально-вертикальной линией связи. Часть этой ломаной заменяют иногда дугой окружности.

Введенная система трех плоскостей проекций П₁, П₂ и П₃ разбивает все про­странство на восемь частей, называемых октантами. Их нумеруют следующим об­разом: слева от профильной плоскости октанты сохраняют нумерацию квадрантов, а справа от плоскости П₃ идут номера 5, 6, 7 и 8. При совмещении плоскостей про­екций передняя часть горизонтальной плоскости опускается вниз, а задняя подни­мается вверх; передняя часть профильной плоскости удаляется от нас направо, а задняя приближается слева.

Множество горизонтальных проекций всех точек пространства назовем по­лем горизонтальных проекций П₁ (соответствующая проекция фигуры называется видом сверху), а множество фронтальных проекций всех точек пространства - по­лем фронтальных проекций П₂ (соответствующая проекция фигуры называется ви­дом спереди или главным видом). Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П₃ (соответствующая проекция фигуры называется видом слева).

Чтобы иметь возможность точного построения комплексных чертежей каких-либо фигур, необходимо уметь задавать положения проекций точек, определяющих данные фигуры, при помощи чисел. Для этого, как известно, следует пользоваться координатным методом. Рассмотрим трехгранник, образованный системой плоскостей проекций П₁, П₂ и П₃. На осях X, У, Z установим единицу измерения е. За начало отсчета примем точку О пересечения трех плоскостей проекций (вершину трехгранника). Положительное направление на каждой оси установим, как показано на рис. Тогда трехгранник OXYZ можем рассматривать как прямоугольную декартову систему координат с коорди­натными осями: Ох - ось абсцисс, Оу - ось ординат, Oz - ось аппликат.

Ломаная ОА₁₂А₁А, определяющая положение точки А относительно коор­динатной системы OXYZ, называется, как, уже было сказано ранее, координатной ломаной линией. Звенья этой ломаной называются отрезками координат: ОА - отрезок абсциссы, А₁₂А₁ - отрезок ординаты, А₁А - отрезок аппликаты точки А. Длины отрезков координат точки А, измеренные установленной единицей длины е, называются координатами точки А:

Координаты точки А можно рассматривать, как ее расстояния до плос­костей проекций, поэтому координаты будут иметь следующие значения: Z_А - высота, Y_A - глубина, Х_A - широта точки А. Координаты точки называются определителем точки.

По заданным координатам точку А(Х_А,Y_A,Z_A) можно построить сле­дующим образом. Сначала с помощью единицы длины е строится отрезок OA₁₂, затем отрезок A₁₂A₁, параллельный оси Y, и, наконец, отрезок А₁А, параллельный оси Z. В результате получаем точку А.

6. Комплексный чертёж прямой линии

Пусть в I четверти расположен отрезок прямой l не параллельный и не перпендикулярный ни к одной из плоскостей проекций. Для построения его ортогональных проекций возьмём на прямой 2 точки и спроецируем их на П₁ и П₂. Полученные проекции точек и определяют искомые проекции отрезка прямой.

Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения.

К прямым частного положения относятся параллельные или ^-ые какой-либо плоскости проекций.

Прямая, //-ая какой-либо плоскости проекций, называется прямой уровня.

//-ая П₁ – горизонталь,

//-ая П₂ – фронталь,

//-ая П₃ – профильная прямая уровня.

Прямая уровня на плоскость проекций, которой она параллельна, проецируется без искажений в натуральную величину. При этом её проекция на этой плоскости с осями координат образует углы, равные углам наклона этой прямой к соответствующим плоскостям проекций.

Для задания профильной прямой уровня необходимо задавать на ней проекции двух точек.

Прямая, ^-я какой-либо плоскости проекций, называется проецирующей прямой.

^-я к П₁ – горизонтально проецирующая,

^-я к П₂ – фронтально проецирующая,

^-я к П₃ – профильно проецирующая.

2 точки, проекции которых на какую-либо плоскость проекций совпадают, называются конкурирующие точки.

Если совпадают горизонтальные проекции – горизонтально конкурирующие.

Из двух горизонтально конкурирующих точек на П₁ будет видна та, фронтальная проекция которой находится выше от оси х₁₂.

Из двух фронтально конкурирующих точек на П₂ будет видна та, горизонтальная проекция которой находится дальше от оси х₁₂.

7. Определение натуральной величины отрезка прямой

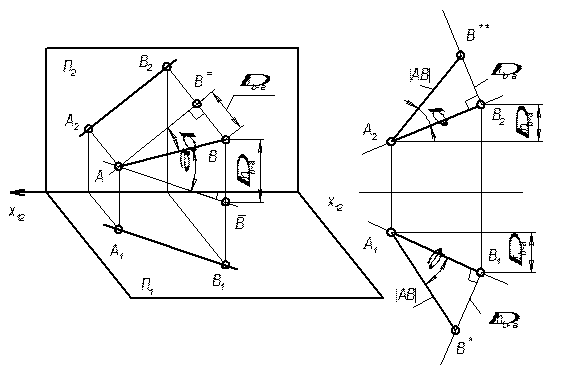
Натуральная величина отрезка прямой является гипотенузой прямоугольного треугольника одним катетом которого служит проекция отрезка на какую-либо плоскость проекций, а другим катетом разность расстояний концов этого отрезка до этой плоскости проекций.

Дата добавления: 2014-01-06