Задачи, для которых не существует полиномиального алгоритма, считаются трудно разрешимыми

Рассмотрим пример определения сложности вычислений (алгоритма) на примерах.

Пусть задано множество S, содержащее n действительных чисел. Требуется найти наибольший и наименьший элементы из S. Положим, что каждое одно сравнение двух любых чисел осуществляется за одинаковое время.

Один из возможных методов состоит в поиске сначала наибольшего элемента из S, а затем – наименьшего. Наибольший элемент можно найти, проводя n-1 сравнений, например по следующему алгоритму.

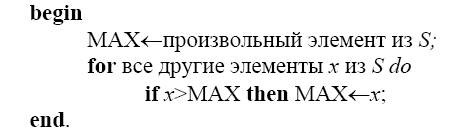
В результате n-1 сравнений найдётся наибольший элемент. Заметим, что не учитывается время на выборку элемента. Далее начинается поиск наименьшего элемента по аналогичному алгоритму. Если считать эти процедуры независимыми, то вновь потребуется n-1 сравнений. В итоге для нахождения наибольшего и наименьшего элементов из S потребуется 2n-2 сравнений.

Число необходимых сравнений можно уменьшить, если использовать принцип «разделяй и властвуй», который в теории алгоритмов называют ещё стратегией дублирования.

Стратегия дублирования состоит в следующем. Пусть размер задачи (размер входных данных задачи) равен n. Разобьём задачу на две подзадачи размера n/2 той же структуры, что и исходная задача. Если решения этих задач можно скомбинировать в решение исходной задачи, то получится эффективный алгоритм.

Рассмотрим, как стратегия дублирования даёт ускорение для решения предыдущей задачи. Положим, что число элементов множества S является степенью числа 2, т.е. n=2k, для некоторого k, k≥1.

Реализуем рекурсивный поиск, при котором множество S разбивается последовательно на два подмножества по следующей процедуре MAXMIN.

В этой процедуре сравнения происходят только на 3-ем шаге, где сравниваются два элемента множества S из которых оно и состоит, и на шаге 7, где сравниваются max1 с max2 и min1 с min2. Пусть Т(n) – число сравнений элементов множества S. Ясно, что Т(2)=1. Если n>2, то Т(n) – общее число сравнений, произведённых в двух вызовах процедуры MAXMIN (строка 5 и 6), работающих на множествах размера n/2 и ещё два сравнения в строке 7. Таким образом,

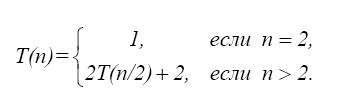
Решением рекуррентных уравнений (7.1) служит функция Т(n)=(3/2)n-2. Таким образом, вместо 2n-2 сравнений получили (3/2)n-2 сравнений чисел, т.е на (n/2) сравнений меньше.

Рассмотрим второй пример. Пусть требуется умножить два n разрядных двоичных чисел. При традиционном (школьном) алгоритме требуется 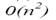битовых операций. Применим стратегию дублирования и разобьем числа х и у на две равные части:

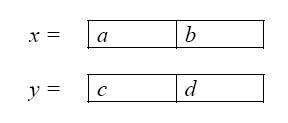
Считаем, что n есть степень числа 2. Тогда

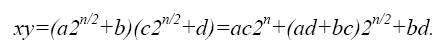
Равенство даёт способ вычисления ху с помощью четырёх умножений (n/2) разрядных чисел и нескольких сложений и сдвигов (умножений на степень числа 2).

Можно получить, что вместо 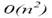битовых операций нужно 0() ≈ 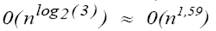битовых операций. Здесь число разбивалось на два блока. Разбивая эти числа на большее число блоков можно получить, что умножение двух чисел имеет сложность 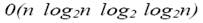для алгоритма Шёнхаге-Штрассена

Абстрактной моделью полиномиального алгоритма является так называемая детерминированная машина Тьюринга. Эта машина в каждый данный момент времени находится в строго определённом состоянии, за один шаг она совершает одно из некоторого конечного множества действий. Затем она переходит в следующее состояние и всё начинается вновь, пока не придёт к ситуации останова.

Дата добавления: 2014-01-07