Лекция №3. Интенсивность отказов. Параметр потока отказов

Напомним, что интенсивностью отказов называют плотность вероятности возникновения отказа объекта, определяемую при условии, что до рассматриваемого момента времени отказ не возник.

Примечание. Интенсивность отказов является показателем безотказности неремонтируемых (и необновляемых) объектов.

Для освоения понятия «интенсивность отказов» рассмотрим следующую задачу. Пусть объект работал безотказно до момента времени t₁. Требуемся определить вероятность отказа объекта на отрезке (t₁,t₂) шириной ∆t = t₂ – t₁.

Сначала определим вероятность того, что объект не откажет в течение времени t₁ + ∆t, то есть совместно произойдут события безотказной работы объекта в течение времени t₁ и ∆t, то есть

p(t₁ + ∆t)=р(t₁)*p(∆t)

где р(∆t) = 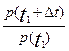- условная вероятность безотказной работы объекта в течение времени t при условии, что в течение времени t₁ объект работает безотказно. Вероятность отказа на отрезке ∆t=(t₁, t₁ + ∆t) есть вероятность противоположного события, то есть

g(t₁, t₁+∆t)=1-.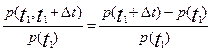

Разделим левую и правую части этого неравенства на ∆t

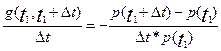
и устремим ∆t к нулю. Используя понятие производной, имеем:

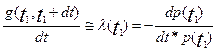(2.31)

Таким образом, интенсивность отказов λ(t₁) в момент времени t₁ есть плотность условной вероятности отказа в момент времени t₁ при условии, что до этого момента объект работал безотказно. В общем случае вместо t₁ можно поставить t, тогда интенсивность отказе обозначается λ(t).

Как видно из соотношения (2.31), физической сущностью λ(t₁) является относительная скорость снижения вероятности безотказной работы объекта.

Разрешая (2.31) относительно p(t₁) и интегрируя, получаем:

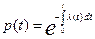. (2.32)

Выражение (2.32) справедливо для любого закона распределения времени безотказной работы объекта, поэтому его называют основным законом надежности.

При λ(t)=const=λ

P(t)=e^-λ(t) .

Интенсивность отказов λ(t) может быть определена по результатам испытаний (рис. 2.7):

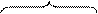∆t

0 t₁ t_g=t₁+∆t t

Рис. 2.7 Определение интенсивности отказов при испытаниях

λ(t)=λ^•(t)=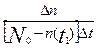. (2.33)

где N₀ – число объектов, подвергнутых испытаниям;

n(t₁) - число объектов, отказавших к моменту времени t₁;

N₀ - n(t₁) - число исправных объектов к моменту времени t₁ (к началу интервала ∆t);

∆n - число объектов, отказавших в течение интервала времени ∆t.

Таким образом, статистическая интенсивность отказов в данный момент времени равна числу отказов в единицу времени, отнесенному к числу не отказавших до этого момента объектов.

На рис. 2.8 представлена типовая зависимость λ(t). Она имеет три характерных участка: убывания интенсивности отказов, ее постоянного значения и возрастания. Соответственно этому вся наработка объекта делится на три периода.

Первый период (до наработки t₁) называется периодом приработки. Снижение интенсивности отказов в этот период связано с выявлением скрытых конструктивно-производственных недостатков: устранение этих недостатков ведет к снижению интенсивности отказов.

Второй период эксплуатации (от наработки t₁ до наработки t₂) является основным и называется периодом нормальной эксплуатации. Отказы, случающиеся в объекте на этом интервале наработки, определяются особенностями конструкции, случайными отклонениями технологии производства от нормативной и условиями эксплуатации.

Третий период эксплуатации (после наработки t₂) является завершающим и называется периодом износа и старения.

λ(t)

t₁ t₂ t

Рис. 2.8 Периоды эксплуатации объекта

Для восстанавливаемых в процессе эксплуатации объектов показателем безотказности является параметр потока отказов, под которым понимается отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку и значению этой наработки. Обозначается этот показатель ω(t).

Параметр потока отказов может быть определен в результате испытаний N₀ объектов, которые после отказа восстанавливаются (ремонтируются). Если за время ∆t произойдет ∆n^• отказов (в общем случае число отказов не равно числу отказавших объектов, так как каждый из восстановленных объектов может отказать несколько раз), то параметр потока отказов в момент времени, соответствующий началу интервала ∆t, равен своей оценке:

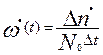(2.34)

В период нормальной эксплуатации

ω^•(t)=const= ω^•,

и вероятность безотказной работы восстанавливаемого объекта в течении времени может быть оценена по формуле:

р(t)=e^-ω˙t. (2.35)

рассмотрим некоторые законы распределения непрерывных случайных величин.

Дата добавления: 2014-01-07