Частные случаи скалярных полей

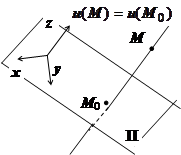Скалярное поле называется плоским, если существует такая плоскость П, что поле принимает одинаковые значения во всех точках прямой, перпендикулярной плоскости П. Другими словами, это поле устроено одинаково во всех плоскостях, параллельных плоскости П. Удачным выбором координатной системы в этом случае будет ввести её так, чтобы плоскость П была плоскостью Оху. Тогда ось Оz будет перпендикулярна П, и, по определению плоского поля, функция u (M) не должна зависеть от z, т.е. u (M) = u (х, у). Поверхности уровня этого поля - цилиндрические поверхности с образующими, перпендикулярными плоскости П; след этих поверхностей в плоскости П даст линии уровня функции u (х, у).

Скалярное поле называется цилиндрическим, если существует такая прямая L, что значения поля u (M) зависят только от расстояния r от точки М до прямой L. Если система координат введена так, что эта прямая - ось Оz, то и u (M)= u (r), т.е. цилиндрическое поле - частный случай плоского поля. Так как 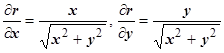, то 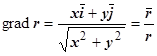, . Понятно, что цилиндрическое поле проще всего описывается в цилиндрических координатах, так как функция u (M) не будет зависить от координат .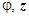

Скалярное поле называется сферическим, если существует такая точка О, что значения поля u (M) зависят только от расстояния r от точки М до точки О. Если точка О взята за начало системы координат, то 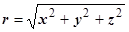и u (M)= u (r). Поверхности уровня сферического поля - сферы с центром в точке О. В этом случае также , . Сферическое поле проще всего описывается в сферических координатах, так как функция u (M) не будет зависить от координат .

17.2. Векторное поле.

17.2.1. Векторное поле. Если каждой точке М некоторой области V пространства соответствует значение некоторой векторной величины 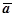(M), то говорят, что в области V задано векторное поле 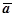(M). Примеры векторных полей - поле тяготения, поля электрической и магнитной напряжённостей, поле скоростей частиц движущейся жидкости.

Если в некоторой декартовой системе координат вектор 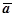(M) имеет координаты Р (M), Q (M), R (M), то 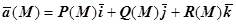. Таким образом, задание векторного поля 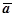(M) эквивалентно заданию трёх скалярных полей Р (M), Q (M), R (M). Будем называть векторное поле гладким, если его координатные функции - гладкие скалярные поля. Кроме того, будем предполать, что векторное поля не имеет особых точек, т.е. 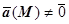при 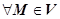, т.е. функции Р, Q, R не равны нулю одновременно.

В зависимости от рассматриваемых вопросов для нас будет более предпочтительной какая-либо одна из двух интерпретаций векторного поля - силовая или гидродинамическая. В силовой интерпретации вектор 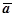(M) трактуется как сила (тяжести, напряжённости, например), действующая в точке М; в гидродинамической интепретации 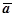(M) рассматривается как поле скоростей текущей в области V несжимаемой жидкости. Как и в случае скалярного поля, мы рассматриваем стационарные векторные поля, т.е. поля, постоянные во времени.

Дата добавления: 2014-01-07