Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана

Рассмотрим основные понятия и выводы специального раздела линейного программирования — теории двойственности.

С каждой задачей линейного программирования определенным образом тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной или прямой.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной ЗЛП.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой задачи. Однако при определении симплексным методом оптимального плана одной из задач находится решение и другой задачи.

Правило построения двойственной задачи по отношению к исходной задаче определяется системой соотношений:

Исходная задача	Двойственная задача

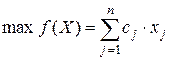
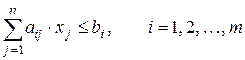
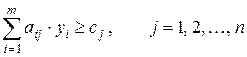
Двойственная задача составляется согласно следующим правилам:

1) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид «£», а в задаче на минимум — «³».

2) матрица, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица в двойственной задаче получаются друг из друга транспонированием;

3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи; число ограничений двойственной задачи равно числу переменных в исходной задаче;

4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;

5) каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства «£», соответствует переменная, связанная условием неотрицательности.

Основные утверждения о двойственных задачах содержатся в двух следующих теоремах

Теорема 1 (основная теорема двойственности). Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны: 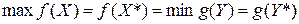. Если одна из двойственных задач неразрешима, то неразрешима и другая.

Теорема 2 (о дополняющей нежесткости). Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i -е ограничение обращается в неравенство, то i -я компонента оптимального плана двойственной задачи равна нулю. Если i -я компонента оптимального плана двойственной задачи положительна, то i -е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.

То есть для оптимальных планов двойственных задач имеют место соотношения:

,

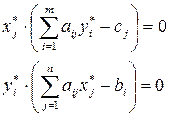которые позволяют, зная оптимальное решение одной из двойственных задач, найти оптимальное решение другой задачи.

Дата добавления: 2014-01-07