Теоремы свертки и запаздывания

Лекция 6.

Теорема. (теорема запаздывания) Если f(t) = 0 при t < 0, то справедлива формула

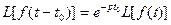
где t₀ – некоторая точка.

Определение. Выражение 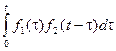называется сверткой функций f₁(t) и f₂(t) и обозначается f₁* f₂.

Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций f₁(t) и f₂(t).

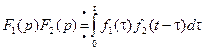
Теорема. (Интеграл Дюамеля (Дюамель (1797 – 1872) – французский математик)). Если , то верно равенство

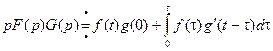
Для нахождения изображений различных функций наряду с непосредственным интегрированием применяются приведенные выще теоремы и свойства.

Пример. Найти изображение функции .

Из таблицы изображений получаем: .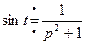

По свойству интегрирования изображения получаем: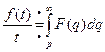

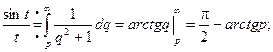
Пример. Найти изображение функции .

Из тригонометрии известна формула .

Тогда =.

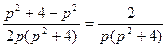Операционное исчисление используется как для нахождения значений интегралов, так и для решение дифференциальных уравнений.

Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.

Требуется найти решение этого дифференциального уравнения, удовлетворяющее начальным условиям:

Если функция x(t) является решением этого дифференциального уравнения, то оно обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция f(t) имеет (по теореме единственности) одно и то же изображение Лапласа.

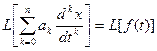
Из теоремы о дифференцировании оригинала {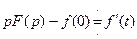} можно сделать вывод, что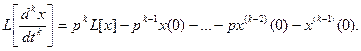

Тогда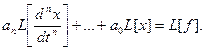

Обозначим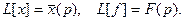

Получаем:

Это уравнение называется вспомогательным (изображающим) или операторным уравнением.

Отсюда получаем изображение , а по нему и искомую функцию x(t).

Изображение получаем в виде: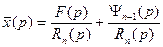

Где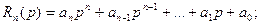

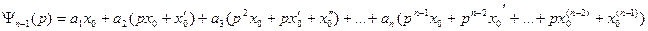Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:

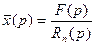
Рассмотрим применение этого метода на примерах.

Пример. Решить уравнение

Изображение искомой функции будем искать в виде:

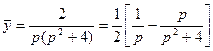
Находим оригинал, т.е. искомую функцию:

Пример. Решить уравнение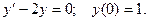

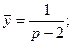
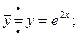
Пример. Решить уравнение:

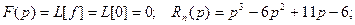
Изображение искомой функции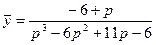

Для нахождения оригинала необходимо разложить полученную дробь на элементарные дроби. Воспользуемся делением многочленов (знаменатель делится без остатка на p – 1):

p³ – 6p² + 11p – 6 p - 1

p³ – p² p² – 5p + 6

-5p² + 11p

-5p² + 5p

6p - 6

6p - 6

В свою очередь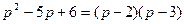

Получаем:

Тогда: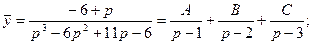

Определим коэффициенты А, В и С.

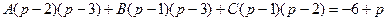
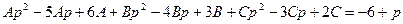
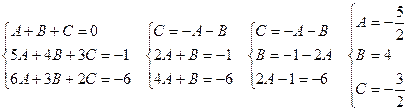
Тогда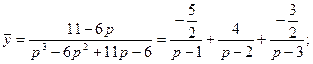

Приемы операционного исчисления можно также использовать для решения систем дифференциальных уравнений.

Пример. Решить систему уравнений:

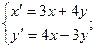
Обозначим 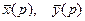- изображения искомых функций и решим вспомогательные уравнения:

Решим полученную систему алгебраических уравнений.

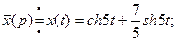
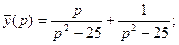
Если применить к полученным результатам формулы

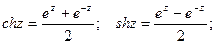
то ответ можно представить в виде:

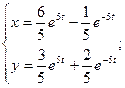
Как видно, гиперболические функции в ответе могут быть легко заменены на показательные.

Пример. Решить систему уравнений

при x(0) = y(0) = 1

Составим систему вспомогательных уравнений:

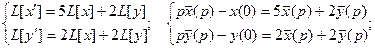
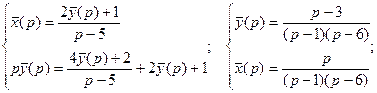
Если обозначить то из полученного частного решения системы можно записать и общее решение:

При рассмотрении нормальных систем дифференциальных уравнений этот пример был решен традиционным способом Как видно, результаты совпадают.

Отметим, что операторный способ решения систем дифференциальных уравнений применим к системам порядка выше первого, что очень важно, т.к. в этом случае применение других способов крайне затруднительно.

Дата добавления: 2014-01-07