Визначники 1, 2 і 3 порядку

План

Лінійна алгебра

Лінійна алгебра вивчає лінійні операції над об’єктами (їх додавання та множення на число), лінійні алгебраїчні рівняння (наприклад, 2х-3у=10) і системи таких рівнянь, а також матриці (масиви).

1. Неповне означення визначника n-порядку.

2. Означення визначників 2 і 3 порядків.

3. Уточнення означення. Перестановки та їх властивості.

4. Властивості визначників. Означення лінійного простору, лінійної залежності та незалежності об’єктів простору.

5. Системи лінійних алгебраїчних рівнянь: основні означення.

6. Теорема Крамера. Теорема про несумісну систему та інші наслідки з теореми Крамера чи з її доведення.

7. Теорема про сумісну систему з головним визначником рівним нулю. Відповідна однорідна система. Зв'язок між розв’язками неоднорідної та відповідної однорідної систем.

8. Наслідки з попередньої теорії для однорідних систем. Властивості її розв’язків.

9. Дослідження в лінійному просторі: максимальна система лінійно незалежних векторів, базис (фундаментальна система) та розмірність. Зведення лінійних операцій в просторі до покоординатних. Лінійний простір n - елементних рядків (стовпців), його розмірність.

10. Знаходження фундаментальної системи розв’язків однорідної системи.

Визначник – допоміжне поняття. Нехай n є ℕ, ℕ={1,2,3,…} – множина натуральних чисел.

Означення 1. (неповне) Визначник n-го порядку записується у вигляді квадратної таблиці чисел або виразів (n×n), обчислюється за таким правилом: додаються всі добутки, в яких є по одному елементу з кожного рядка і з кожного стовпчика, при цьому деякі добутки беруть із знаком «+», деякі – із знаком «-».

Означення неповне, бо не вказано, які саме добутки брати з якими знаками.

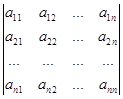= Таблиця в прямих дужках. Перший індекс – номер рядка. Другий індекс – номер стовпця.

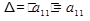Приклад.

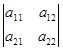= = a ₁₁ a ₂₂ – a ₁₂ a ₂₁

Приклад. ,

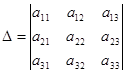= a ₁₁ а ₂₂ а ₃₃ +а ₂₁ а ₃₂ а ₁₃ + а ₁₂ а ₂₃ а ₃₁ – а ₁₃ а ₂₂ а ₃₁ – а ₂₃ а ₃₂ а ₁₁ – а ₁₂ а ₂₁ а _33. (1)

Називається правило трикутника.

Приклад. 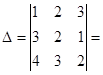4+8+27-24-12-3=39-39=0.

Правило Сар’юса: дописують до визначника справа його перший і другий стовпчики:

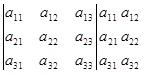
- - - + + + Переконуємось, що вийде такий ж вираз як і за правилом

трикутника.

Уточнення означення.

Означення. Перестановка з n чисел – це числа від 1 до n розміщені в деякому порядку. Перестановки відрізняються порядком елементів.

Приклад. 3,1,2,4 та 4,1,3,2 – дві перестановки з чотирьох чисел.

Означення. Кількість інверсій перестановки — це кількість пар елементів, в яких більший елемент розміщений в перестановці перед меншим. Якщо кількість інверсій перестановки парна то перестановка називається парною, якщо непарна — непарною.

Зауваження. В перестановці з будь-яких n натуральних чисел аналогічно вводиться кількість інверсій та парність.

Перестановка 1,2,3,…, n називається натуральною. Очевидно, що вона парна.

Розглянемо формулу обчислення визначника третього порядку (1). Якщо в кожному добутку розмістити перші індекси в порядку зростання (тобто записувати множники в добутку по порядку рядків), то другі індекси утворять перестановку з трьох чисел. Визначимо кількості інверсій та парність перестановки для кожного добутку:

1) a ₁₁ а ₂₂ а ₃₃ -- 1,2,3 0 інверсій – парна

2) а ₂₁ а ₃₂ а ₁₃ = а ₁₃ а ₂₁ а ₃₂ -- 3,1,2 2 інверсії (пари 3,1 та 3,2) - парна

3) а ₁₂ а ₂₃ а ₃₁ -- 2,3,1 2 інверсії (пари 2,1 та 3,1) - парна

4) а ₁₃ а ₂₂ а ₃₁ -- 3,2,1 3 інверсії (пари 3,2; 3,1 та 2,1) - непарна

5) а ₂₃ а ₃₂ а ₁₁ = а ₁₁ а ₂₃ а ₃₂ -- 1,3,2 1 інверсія (пара 3,2) - непарна

6) а ₁₂ а ₂₁ а ₃₃ -- 2,1,3 1 інверсія (пара 2,1) – непарна

Отже, ті добутки, яким відповідає парна перестановка, беруть із знаком «+», а яким непарна – із знаком «-».

Закінчення означення визначника n – го порядку. Для кожного добутку в розкладі визначника визначають відповідну перестановку. Ті добутки, яким відповідають парні перестановки, беруть із знаком «+», а яким непарні – беруть із знаком «-».

Зауваження. Добутку на головній діагоналі відповідає натуральна перестановка, тому добуток з головної діагоналі завжди буде із знаком «+».

Властивості перестановок (Воеводин. Линейная алгебра, стор.122)

1. При перестановці двох елементів перестановка змінює парність. Назвемо таку операцію транспозицією.

Доведення. При перестановці двох сусідніх елементів очевидно, що змінюється кількість інверсій на одиницю, тобто зміниться парність. Нехай поміняли місцями елементи i та j (i був попереду j), між якими було k елементів. Цю зміну можна зробити переставляючи i з сусідніми поки він не стане після j. Буде k+1 змін парності. Потім j переміщувати вперед, переставляючи з попередніми, поки він не стане на місце i. Буде k змін парності. Разом 2k+1 зміни парності, тому перестановка змінить парність.

2. Всі перестановки з n елементів можна розмістити в такому порядку, що кожна наступна перестановка відрізнятиметься від попередньої тільки однією транспозицією. Починати можна з будь-якої перестановки.

Доведення. Метод математичної індукції. При n=2 можна: 1,2; 2,1 або 2,1; 1,2. Припустимо, що при всіх n від 2 до деякого k>2 це можна зробити і доведемо для n=k+1. При такому n почнемо з будь-якої перестановки, в якої буде на першому місці деякий елемент. Всі елементи крім першого утворюватимуть перестановку з k елементів. Будемо робити транспозиції, не змінюючи першого елемента, поки не вичерпаємо всі такі перестановки, це можливо за припущенням індукції. Тоді поміняємо місцями перший елемент з деяким іншим, і повторимо операцію. Продовжуватимемо до тих пір, поки на першому місці не побувають всі числа.

Отже, при n³2 кількості парних і непарних перестановок однакові, тому кількості добутків із знаком «+» та «-» у визначнику при таких n однакова.

Із першої та другої властивостей випливає третя.

3. Нехай є дві перестановки з n елементів, перша з яких натуральна. Якщо зводити другу перестановку до натуральної шляхом транспозицій, і при кожній транспозиції робити будь-яку транспозицію в першій перестановці, то при закінченні процесу парність першої перестановки буде така якою була парність другої на початку процесу.

Далі ми навчимось з допомогою властивостей визначників зводити визначники вищих порядків до визначників 3-го і 2-го порядків.

Дата добавления: 2014-01-06