
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наслідки з теореми Крамера чи з її доведення
|
|
|
|
Теорема про несумісну систему. Якщо в квадратній системі головний визначник дорівнює нулю, а хоча б один з допоміжних визначників Δі не дорівнює нулю, то система несумісна.
Доведення. Аналогічно як в доведенні теореми Крамера, отримаємо рівняння
xіΔ=Δі, яке очевидно не має розв’язків.
 Пр. 3х-4y+5z=-2 Квадратна система лінійних алгебраїчних рівнянь (3х3).
Пр. 3х-4y+5z=-2 Квадратна система лінійних алгебраїчних рівнянь (3х3).
2x+3y-z=1 Можна дослідити з допомогою визначників.
x-7y+6z=1
|

 =
=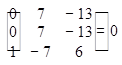 (однакові рядки).
(однакові рядки).
Не можна використати метод Крамера.


|
 =
=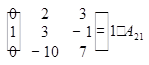 =
=
=1(-1) -- система не має розв’язків.
-- система не має розв’язків.
Відповідь. Ø.
Теорема (про обведений мінор чи про залежне рівняння). Якщо 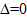 і деякий допоміжний визначник
і деякий допоміжний визначник  , але деякий мінор головного визначника не дорівнює нулю
, але деякий мінор головного визначника не дорівнює нулю 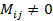 , то і -те рівняння буде залежним від інших і його можна не враховувати.
, то і -те рівняння буде залежним від інших і його можна не враховувати.
Доведення. Домножимо і- те рівняння на алгебраїчне доповнення Аij (Аij ¹0) і додамо до нього інші рівняння системи, домножені на відповідні алгебраїчні доповнення до j- го стовпчика у D:




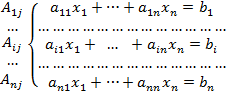
Отримаємо еквівалентну систему. На місці і-го рівняння буде рівняння  , тобто
, тобто 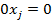 , а таке рівняння можна відкинути.
, а таке рівняння можна відкинути.
Після відкидання отримуємо нову систему, в якій рівнянь менше ніж невідомих.
Теорема (рівнянь менше ніж невідомих). Якщо рівнянь є k, а невідомих є n, k<n та існує визначник D, побудований із k стовпчиків коефіцієнтів біля невідомих не рівний нулю (D¹0) то система має безліч розв’язків.
Доведення. Доведемо на прикладі системи з двома рівняннями: 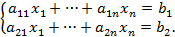
Нехай визначник, побудований із деяких двох стовпчиків коефіцієнтів при невідомих, не дорівнює нулю.
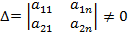
Доведемо, що тоді система має безліч розв’язків.
Залишимо ці стовпчики зліва, а інші доданки перенесемо в правий бік.
|
|
|
Вважатимемо невідомі перенесені вправо – параметрами.
Невідомих залишилось 2. Тоді система буде квадратною, її головний визначник буде не рівним нулю, тобто при будь-яких значеннях параметрів буде один розв’язок (отже, їх буде безліч). Очевидно, що доведення годиться для будь-якої кількості рівнянь.
Приклад.
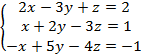


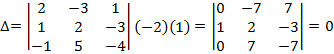 , бо є пропорційні рядки.
, бо є пропорційні рядки.
 ;
;  ;
;  , бо є однакові стовпчики. Висновок: розв’язків безліч, або немає.
, бо є однакові стовпчики. Висновок: розв’язків безліч, або немає.
 – отже, третє рівняння залежне і його можна не враховувати (уважно роздивившись побачимо, що 3р.=2р. - 1р.).
– отже, третє рівняння залежне і його можна не враховувати (уважно роздивившись побачимо, що 3р.=2р. - 1р.).
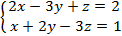 . Ми знаємо, що визначник, складений із перших двох стовпчиків при невідомих не дорівнює нулю. Перенесемо доданки третього стовпчика вправо і вважатимемо z параметром.
. Ми знаємо, що визначник, складений із перших двох стовпчиків при невідомих не дорівнює нулю. Перенесемо доданки третього стовпчика вправо і вважатимемо z параметром.

 - будь-які значення.
- будь-які значення.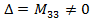 (розв’язків безліч)
(розв’язків безліч)
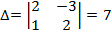 ,
, 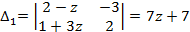 ,
,  =7z
=7z


Відповідь. 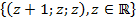 .
.
Теорема. При 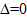 якщо є один розв’язок, то їх буде безліч.
якщо є один розв’язок, то їх буде безліч.
 . Позначимо його стовпчики р1=
. Позначимо його стовпчики р1= , р2=
, р2=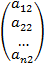 ,…
,…
Стовпчики головного визначника р1,р2 … pn – лінійно залежні, тобто є такі не всі рівні нулю числа 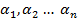 , що
, що
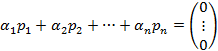
Нехай набір чисел 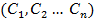 - є розв’язком, тобто:
- є розв’язком, тобто:
 .
.
Тоді набір чисел ( ) очевидно теж буде розв’язком (новий розв’язок).
) очевидно теж буде розв’язком (новий розв’язок).
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1080; Нарушение авторских прав?; Мы поможем в написании вашей работы!