
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 28
Функції на векторних (лінійних) просторах.
Означення 28.1 Функція одного векторного аргументу це: ‹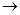 ú(або ÷). (Якщо ‹ - дійсний векторний простір, то обирається множина ú, якщо ‹ - комплексний векторний простір, то обирається множина ÷).
ú(або ÷). (Якщо ‹ - дійсний векторний простір, то обирається множина ú, якщо ‹ - комплексний векторний простір, то обирається множина ÷).
Означення 28.2 Функція двох векторних аргументів називається: ‹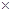 ‹
‹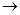 ú(або ÷).([1])
ú(або ÷).([1])
Зауваження 28.1 Функції на нескінченно вимірних векторних просторах прийнято називати функціоналами.
§ 1 Лінійні функції одного аргументу (лінійні форми).
Означення 28.3 Функція L одного векторного аргументу називається лінійною, якщо
1) 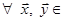 ‹ L (
‹ L (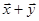 )= L (
)= L ( ) + L (
) + L (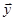 ) (властивість адитивності),
) (властивість адитивності),
2) 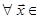 ‹,
‹, 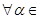 ú(або ÷). L (
ú(або ÷). L (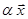 )=
)=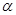 L (
L ( ) (властивість однорідності).
) (властивість однорідності).
Іншими словами: лінійна функція одного аргументу це адитивна та однорідна скалярна функція векторного аргументу.
Зауваження 28.2 Лінійна функція це частинний випадок лінійного відображення. А саме - лінійне відображення даного векторного простору ‹ в одномірний арифметичний простір ú(або ÷).
Розглянемо n - вимірний векторний простір і виберемо в ньому базис 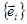 . Тоді
. Тоді 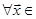 ‹n
‹n 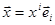 , де
, де 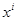 - координати вектора
- координати вектора  в базисі
в базисі 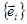 , а L (
, а L ( )= L (
)= L (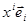 )= L (
)= L (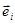 )
)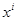 . Позначимо L (
. Позначимо L (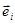 )=
)=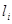 ,
, 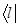 - матрицю-рядок з елементами
- матрицю-рядок з елементами 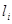 ,
, 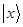 - матрицю-стовпчик координат вектора
- матрицю-стовпчик координат вектора  . Остаточно маємо
. Остаточно маємо
L ( )=
)=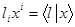 (28.1)
(28.1)
Зауваження 28.3 Числа 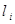 = L (
= L (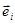 ) не залежать від вектора
) не залежать від вектора  , а визначаються тільки функцією L і базисними векторами
, а визначаються тільки функцією L і базисними векторами 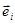 .
.
Ми довели наступне
Твердження 28.1 Будь-яка лінійна функція на ‹n в довільному базисі задається лінійним однорідним многочленом (28.1) від координат вектора по цьому базису.
Значення функції L (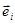 )=
)=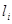 називаються компонентами або коефіцієнтами функції L в базисі
називаються компонентами або коефіцієнтами функції L в базисі 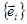 .
.
Розглянемо два базиси 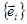 та
та 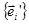 в просторі ‹n. Ці базиси пов’язані між собою співвідношеннями ()
в просторі ‹n. Ці базиси пов’язані між собою співвідношеннями () 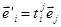 (
(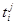 - елементи матриці переходу Т від базису
- елементи матриці переходу Т від базису 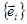 до базису
до базису 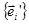 ). Тоді
). Тоді 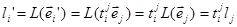 . Або
. Або
 . (28.2)
. (28.2)
§ 2 Білінійні форми.
Означення 28.4 Білінійною формою або білінійною функцією на векторному просторі ‹n називається функція В від двох векторів на ‹n, яка задовольняє вимогам
1) 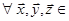 ‹n
‹n 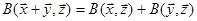 ,
,
2) 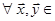 ‹n,
‹n, 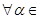 ú(або ÷)
ú(або ÷) 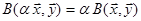 ,
,
3) 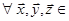 ‹n
‹n 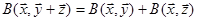 ,
,
4) 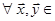 ‹n,
‹n, 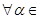 ú(або ÷)
ú(або ÷) 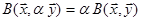 .
.
Іншими словами: білінійна форма це скалярна функція двох векторних аргументів адитивна та однорідна по обом своїм аргументам.
Виберемо в просторі ‹n базис 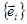 . Якщо
. Якщо 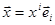 ,
, 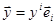 , то значення білінійної форми В на векторах
, то значення білінійної форми В на векторах  і
і 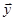 може бути обчислено наступним чином
може бути обчислено наступним чином 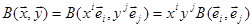 . Позначимо
. Позначимо 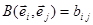 - значення білінійної форми на всеможливих парах базисних векторів. Числа
- значення білінійної форми на всеможливих парах базисних векторів. Числа 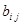 - називаються коефіцієнтами білінійної форми в базисі
- називаються коефіцієнтами білінійної форми в базисі 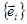 , а матриця
, а матриця 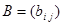 - матрицю білінійної форми в даному базисі. Тоді остаточно
- матрицю білінійної форми в даному базисі. Тоді остаточно
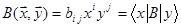 (28.3)
(28.3)
При заміні базису матриця білінійної форми змінюється. Отримаємо закон її зміни.
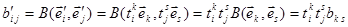 .
.
Або
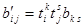 і в матричному вигляді
і в матричному вигляді 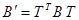 . (28.4)
. (28.4)
Означення 28.5 Білінійна форма називається симетричною, якщо 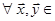 ‹n
‹n 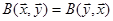 .
.
Твердження 28.2 (Критерій симетрії білінійної форми). Для того щоб білінійна форма була симетрична необхідно і достатньо щоб вона в деякому базисі мала симетричну матрицю (тоді вона буде мати симетричну матрицю і в будь якому базисі).
Необхідність ◄ Нехай білінійна форма симетрична 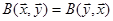 , тоді
, тоді 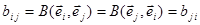 . Або
. Або 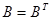 ►
►
Достатність ◄ Нехай в деякому базисі матриця білінійної форми симетрична - 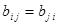 . Тоді
. Тоді 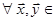 ‹n
‹n 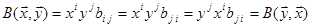 . Так як білінійна форма симетрична, то вона буде мати симетричну матрицю і в будь якому базисі. ►
. Так як білінійна форма симетрична, то вона буде мати симетричну матрицю і в будь якому базисі. ►
§ 3 Квадратичні форми.
Означення 28.6 Квадратичною формою називається функція 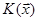 на векторному просторі ‹n (
на векторному просторі ‹n (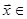 ‹n), значення якої
‹n), значення якої 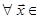 ‹n визначається рівністю
‹n визначається рівністю  , де В - симетрична білінійна форма на ‹n.
, де В - симетрична білінійна форма на ‹n.
Білінійну форму В, яка фігурує в означенні 28.6 будемо називати породжуючою квадратичну форму K.
По квадратичній формі K можна однозначно поновити ту білінійну форму, яка її породила. Дійсно, 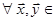 ‹n
‹n 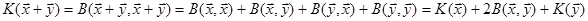 . Звідки
. Звідки
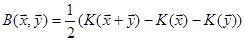 (28.5)
(28.5)
Зауваження 28.4 При отримані співвідношення (28.5) ми суттєво використали вимогу симетрії білінійної форми.
Зауваження 28.5 Матриця симетричної білінійної форми В, яка фігурує в означенні 28.6, називається матрицею відповідної квадратичної форми K.
Згідно (28.3) значення 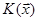 квадратичної форми K записується через координати вектора
квадратичної форми K записується через координати вектора  в деякому базисі в наступний спосіб
в деякому базисі в наступний спосіб
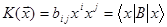 (28.6)
(28.6)
Права частина (28.6) - однорідний многочлен другої степені відносно 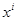 . Приведений його запис містить подібні члени. А саме, при
. Приведений його запис містить подібні члени. А саме, при 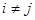 члени
члени 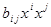 (без сумування по i, j) і
(без сумування по i, j) і 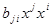 (без сумування по i, j) співпадають. Тому (28.6) можна переписати у вигляді
(без сумування по i, j) співпадають. Тому (28.6) можна переписати у вигляді
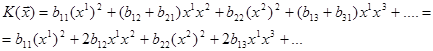 (28.7)
(28.7)
Зауваження 28.6 Саме для того, щоб по многочлену (28.7) можна було б поновити матрицю квадратичної форми і накладається в означені 28.6 умова симетрії білінійної форми, яка породжує квадратичну.
Означення 28.7 Квадратична форма називається діагональною, якщо її матриця має діагональний вид 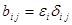 . Тоді сама квадратична форма містить тільки квадрати координат вектора
. Тоді сама квадратична форма містить тільки квадрати координат вектора  :
:
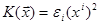 . (28.8)
. (28.8)
Теорема 28.1 Для кожної квадратичної форми існує базис в якому вона має діагональний вигляд.
Доведення проведемо індукцією по розмірності простору ‹n.
◄1) При n=1 в будь якому базисі квадратична форма має діагональний вигляд.
2) Припустимо, що теорема має місце в просторі розмірності n-1.
3) Розглянемо квадратичну форму в просторі розмірності n
В довільному базисі 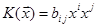 . Можливо, що всі
. Можливо, що всі 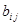 дорівнюють нулю, але в цьому випадку квадратична форма вже має діагональний вигляд. Тому, ми можемо обмежитись випадком, коли хоча б один із коефіцієнтів відмінний від нуля. Не зменшуючи загальності, будемо вважати, що
дорівнюють нулю, але в цьому випадку квадратична форма вже має діагональний вигляд. Тому, ми можемо обмежитись випадком, коли хоча б один із коефіцієнтів відмінний від нуля. Не зменшуючи загальності, будемо вважати, що 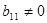 . Дійсно, якщо
. Дійсно, якщо 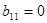 , але
, але 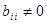 при деякому
при деякому 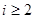 , ми можемо поміняти нумерацію базисних векторів, тобто зробити заміну базису. Якщо
, ми можемо поміняти нумерацію базисних векторів, тобто зробити заміну базису. Якщо 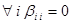 , то у випадку необхідності змінюючи нумерацію базисних векторів, ми можемо вважати
, то у випадку необхідності змінюючи нумерацію базисних векторів, ми можемо вважати 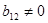 . Зробимо допоміжну заміну базису, таку щоб
. Зробимо допоміжну заміну базису, таку щоб 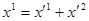 ,
, 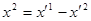 ,
, 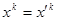 ,
, 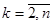 . Такій заміні базису відповідає матриця переходу
. Такій заміні базису відповідає матриця переходу 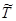 , а її обернена матриця має вигляд
, а її обернена матриця має вигляд
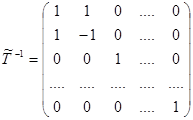 .
.
Після такої заміни базису в квадратичну форму 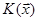 ввійдуть члени
ввійдуть члени 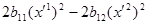 і
і 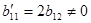 . Таким чином, в разі потреби зробивши заміну базису, можна завжди вважати, що
. Таким чином, в разі потреби зробивши заміну базису, можна завжди вважати, що 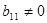 .
.
Зберемо разом члени, які містять 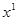 :
:
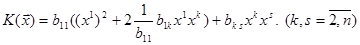
Інакше це можна переписати у вигляді
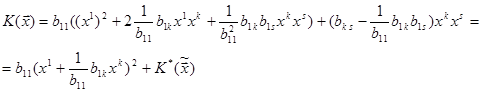
Квадратична форма
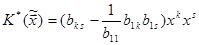
задана в просторі розмірності n-1 і згідно припущенню індукції існує базис в просторі розмірності n-1 в якому квадратична форма 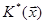 має діагональний вигляд
має діагональний вигляд

Позначимо елементи оберненої матриці переходу до цього базису (в просторі розмірності (n-1)) через 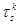 .
.
Покладемо
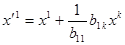 ,
,
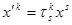
і отримаємо для квадратичної форми K діагональний вигляд. Перехід до нового базису здійснюється з допомогою матриці переходу T, а заміна координат векторів з допомогою матриці 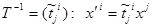 , де
, де

(зірочками позначені елементи значення яких не важливе).►
Зауваження 28.7 Застосований при доведені теореми 28.1 спосіб приведення квадратичної форми до діагонального вигляду має назву метода виділення квадратів Лагранжа і може бути застосований для практичного приведення квадратичної форми до діагонального вигляду.
Означення 28.8 Діагональний вигляд квадратичної форми в дійсному векторному просторі називається канонічним виглядом, якщо коефіцієнти 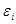 можуть приймати тільки значення +1, -1, 0. В комплексному векторному просторі діагональний вигляд квадратичної форми - канонічний, якщо
можуть приймати тільки значення +1, -1, 0. В комплексному векторному просторі діагональний вигляд квадратичної форми - канонічний, якщо 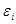 може дорівнювати тільки 1 або 0.
може дорівнювати тільки 1 або 0.
Теорема 28.2 Для кожної квадратичної форми існує базис, в якому вона має канонічний вигляд.
◄ Для початку приведемо квадратичну форму до діагонального вигляду (теорема 28.1). Потім замінимо базис в такий спосіб, щоб: координати векторів, яким відповідають коефіцієнти квадратичної форми 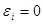 , залишались без змін (
, залишались без змін (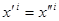 ), а для інших координат
), а для інших координат 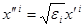 (без сумування по і) в випадку комплексного векторного простору і
(без сумування по і) в випадку комплексного векторного простору і 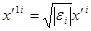 (без сумування по і) в випадку дійсного векторного простору. ►
(без сумування по і) в випадку дійсного векторного простору. ►
Ранг, індекс, визначеність квадратичних форм
Існує багато базисів, в яких квадратична форма має канонічний вигляд. Виявляється, що всі канонічні вигляди квадратичної форми (з точністю до нумерації координат вектора) однакові.
Теорема 28.3. Ранг матриці квадратичної форми не залежить від базису.
◄ Згідно (28.4) в базисі 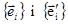 матриці квадратичних форм пов’язані співвідношенням
матриці квадратичних форм пов’язані співвідношенням 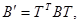 де матриця переходу Т не вироджена. Звідси
де матриця переходу Т не вироджена. Звідси
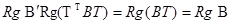 (1) ►
(1) ►
Якщо квадратична форма має канонічний вигляд, то ранг її матриці просто дорівнює кількості коефіцієнтів 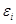 відмінних від нуля. Це число не залежить від базису.
відмінних від нуля. Це число не залежить від базису.
Означення 28.8. Рангом квадратичної форми називається ранг її матриці.
В комплексному векторному просторі всі квадратичні форми одного і того ж рангу 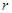 приводяться (кожна в своєму базисі) до одного і того ж канонічного вигляду
приводяться (кожна в своєму базисі) до одного і того ж канонічного вигляду
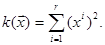
Тепер розглянемо квадратичні форми в дійсному векторному просторі.
Означення 28.9. Квадратична форма 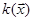 є додатна на підпросторі ‹'
є додатна на підпросторі ‹' 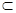 ‹n, якщо
‹n, якщо
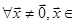 ‹'
‹' 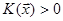
Зауваження 28.8. Окремо відмітимо, що будь-яка квадратична форма 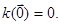
Означення 28.10. Квадратична форма 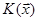 називається від’ємною визначеною на підпросторі ‹'
називається від’ємною визначеною на підпросторі ‹' 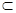 ‹n, якщо
‹n, якщо 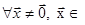 ‹'
‹' 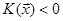
Зауваження 28.9. Якщо ‹' 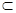 ‹n, то про знакоозначені квадратичні форми просто говорять – додатньо означена, чи від’ємно означена, відповідно.
‹n, то про знакоозначені квадратичні форми просто говорять – додатньо означена, чи від’ємно означена, відповідно.
Означення 28.11. Квадратична форма 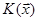 називається додатньо напівозначеною, якщо
називається додатньо напівозначеною, якщо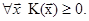
Означення 28.12. Квадратична форма 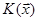 називається від’ємно напівозначеною, якщо
називається від’ємно напівозначеною, якщо
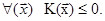
Зауваження 28.10. Якщо 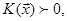 то
то 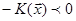 і, відповідно,
і, відповідно, 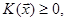 то
то 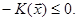
Приклади 28.1. Нехай n=2. Тоді 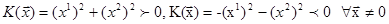 ,
,
а 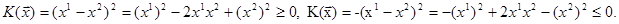
|
Дата добавления: 2014-01-07; Просмотров: 688; Нарушение авторских прав?; Мы поможем в написании вашей работы!