Виды движения

Лекция 2

1.2.1. Равномерное, прямолинейное

Движение называется равномерным и прямолинейным, если точка движется по прямой линии с постоянной скоростью .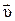

Рассмотрим движение материальной точки с постоянной скоростью вдоль оси OX (рис. 1.8). Пусть в начальный момент времени t=0 координата точки х = х₀, а скорость 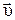совпадает с направлением движения.

Найдем координату х и путь s, пройденный точкой за интервал времени t.

За малый интервал dt перемещение точки

,

где – проекция вектора скорости 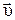на ось ОХ.

Проинтегрируем левую и правую часть последнего равенства в пределах изменения переменных x и t

,

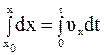, (1.19)

.

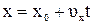В случае когда вектор скорости не совпадает с направлением движения

.

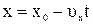При прямолинейном равномерном движении пройденный точкой путь

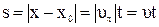. (1.20)

1.2.2 Равнопеременное прямолинейное

Движение называется равнопеременным и прямолинейным, если тело перемещается по прямой линии с постоянным ускорением 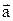. Равнопеременное прямолинейное движение может быть равноускоренным, когда вектор ускорения совпадает с вектором мгновенной скорости и равнозамедленным, когда ему противоположен (рис. 1.9).

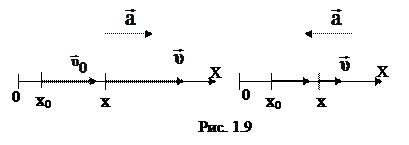
Пусть в начальный момент времени координата точки x=х₀, скорость совпадает с направлением оси ОХ, тогда

при равноускоренном движении ,равнозамедленном .

За время t пройденный точкой путь.

, (1.21)

где – модуль проекции вектора скорости на ось OX находится из соотношения интегрированием его левой и правой части в пределах изменения переменных и t

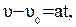
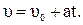
При подстановки в соотношение (1.19) скорости для равноускоренного движения пройденный путь

,

координата точки

. (1.22)

Для равнозамедленного движения проекция скорости и координата точки определяются по формулам

.

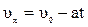. (1.23)

Путь пройденной точкой

где .

1.2.3 Равнопеременное

Движение называется равнопеременным, если тело перемещается по тра­ек­то­рии с постоянным вектором ускорения.

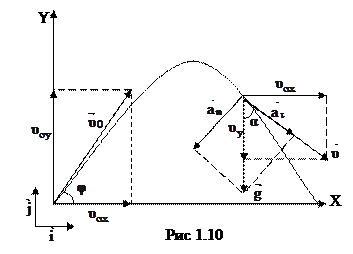
Примером равнопеременного криволинейного движения является движение тела брошенного со скоростью под углом к горизонту (рис. 1.10) Движение тела происходит в гравитационном поле Земли с постоянным ускорением свободного падения . Для определения положения тела в пространстве разложим его движение на равномерное прямолинейное по оси OX со скоростью и равнопеременное по оси OY с ускорением свободного падения g и начальной скоростью .

В момент времени t координаты тела

(1.25)

вектор скорости

. (1.26)

Модуль вектора скорости

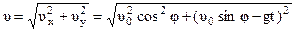, (1.27)

где .

Уравнение траектории найдём путем исключения параметра t из равенств (1.25)

. (1.28)

Ускорение свободного падения в любой точке траектории можно разложить на его касательную и нормальную составляющие, где модуль касательного ускорения

, (1.29)

где α-угол между векторами скорости и ускорения g в заданной точке траектории

Модуль нормального ускорения

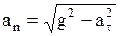. (1.30)

Из сравнения уравнения параболы и равенства (1.28) следует, что тело, брошенное под углом к горизонту, движется по параболе.

Задания для самоконтроля знаний.

1. Определить путь пройденный автомобилем за 2 часа его движения со скоростью 90 км/ч.

2. Определить время обгона легковым автомобилем грузовика, если водитель совершает этот маневр при начальной скорости 80 км/ч с ускорением 2 м/с².

3. Определить тормозной путь поезда движущегося со скоростью 36 км/ч при времени торможения 1 минуты.

4. Определить максимальную высоту подъема снаряда имеющего начальную скорость 100м/с и выкатившего из орудия под углом 45° к горизонту.

Лекция 3

1.2.4 Равномерное, вращательное

Рассмотрим движение м.т. по окружности радиусом R с постоянной линейной скоростью вокруг неподвижной оси Z (рис. 1.11).

Положение точки определяет радиус-вектор 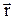. За малый интервал времени радиус-вектор повернется на угол 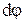. Направление поворота м.т. вокруг оси Z задается вектором и правилом правого винта: поступательное движение правого винта и вектора совпадают, если вращение точки и винта совершается в одинаковом направлении. Модуль вектора равен углу поворота за интервал времени . Линейное перемещение вектора за время dt

(1.31)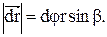

где 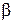– угол между вектором и вектором .

Вектор линейной скорости движения точки

, (1.32)

где – вектор угловой скорости.

Вектор угловой скорости совпадает с направлением вектора ).

Модуль вектора линейной скорости

. (1.33)

Вектор линейного ускорения

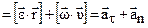, (1.34)

где – вектор углового ускорения, – вектор касательного ускорения, – вектор нормального ускорения.

Направление вектора углового ускорения 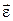совпадает с направлением вектора 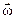(), если угловая скорость возрастает, и противоположно (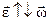), если она уменьшается.

Модули векторов ,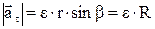

.

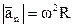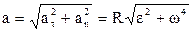. (1.35)

Угловой путь м.т., движущейся по окружности за время dt

.

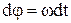Угловой путь 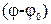точки за интервал времени t при начальном угле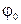

.

При постоянной угловой скорости , угловой путь и угол поворота определяется из равенств:

,

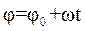. (1.36)

При равноускоренном вращении точки для t=0, 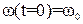, угловая скорость определяется из соотношения

,

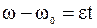
Для равноускоренного вращения за время t угловой путь и угол поворота определяются из соотношений

,

,

,

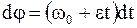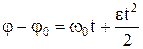. (1.37)

Для равнозамедленного вращения

,

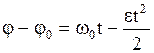, (1.38)

.

Согласно определению угловая скорость измеряется в рад/с, угловое ускорение – рад/с².

1.2.5 Колебательное движение

Колебания — это любой физический процесс, характери­зующийся повторяемостью во времени.

В процессе колебаний значения физических величин, определяющих состояние системы, через равные или неравные промежутки времени повторяются.

Колебания называются периодическими, если движение тела повторяется через равные промежутки времени.

Наименьший промежуток времени Т, через который значение изменяющейся физической величины повторяется (по величине и направлению, если эта величина векторная, по величине и знаку, если она скалярная), называется периодом колебаний этой величины.

Число полных колебаний, совершаемых колеблющейся величиной за единицу времени, называется частотой колебаний и обозначается ν. Период и частота колебаний связаны соотношениями .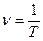

Простейшим из периодических колебаний являются гармонические колебания.

Гармонические колебания - это колебания, в которых координаты тел изменяются с течением времени по закону синуса или косинуса.

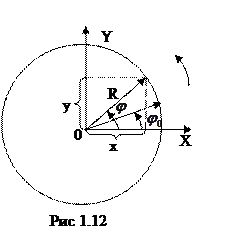
Примером гармонического колебательного движения является изменение координат материальной точки, движущейся по окружности радиусом R (рис. 1.12).

В системе отсчета связанной с центром окружности координаты точки и ее угловой путь определяются:

(1.39)

где φ₀ – угол между радиус-вектором 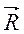и одной из координат системы отсчета в момент времени t = 0.

Подставим в первые два уравнения системы (1.39) вместо , тогда

(1.40)

где – фаза колебания;

φ₀ – начальная фаза колебания;

– циклическая частота.

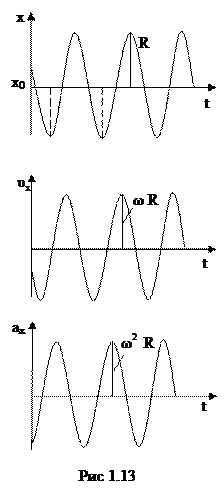
Скорость материальной точки вдоль оси X и Y

(1.41)

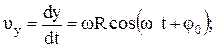(1.42)

ускорения:

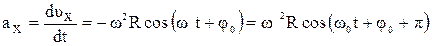
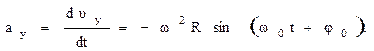(1.43)

При гармонических колебаниях проекции скорости и ускорения изменяются с течением времени по гармоническому закону, с той же частотой , с какой происходят колебания координат (рис. 1.13).

Максимальная амплитуда колебаний скорости вдоль осей координат 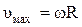, ускорения 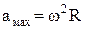. Скорость опережает координату по фазе на , а ускорение на .

Начальная координата x₀, и скорость гармонических колебаний

(1.44)

где А- амплитуда, равная максимальному значению координаты x.

Возведем в квадрат левую и правую часть равенств (1.44) и выделим cos²φ₀ и sin² φ₀

Сложим в системе уравнений левые и правые части и после преобразований получим формулы для вычислений А и φ₀.

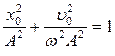или

, (1.45)

.

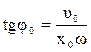Дата добавления: 2014-01-07