Операторная (символическая) форма записи уравнения элемента

Лекция 5

3. Формы представления математических моделей звеньев

Уравнение звена (5), полученное в результате линеаризации

(*)

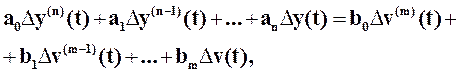где и 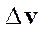- отклонения выхода и входа относительно состояния равновесия (рабочей точки), записывают в различном формате.

Введем в рассмотрение оператор дифференцирования 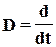, обладающий тем свойством, что его умножение на любую функцию x(t) эквивалентно дифференцированию этой функции по времени:

.

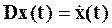Повторное умножение эквивалентно повторному дифференцированию:

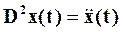
и вообще для любого целого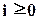

.

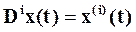Обозначая ради простоты записи 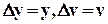, представим уравнение (*) так:

. (1)

Вводя операторные обозначения для производных входа и выхода, и затем вынося y и v за скобку, получаем операторную форму уравнения линейного звена в компактном виде

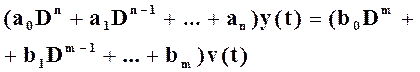
или еще короче

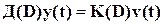, (2)

где входной оператор

и выходной оператор

представляют собой операторные многочлены.

Пример. Рассмотрим вращающийся вал.

Введем следующие обозначения:

- скорость вращения вала, M(t) – суммарный момент, приложенный к валу. Пусть v(t) ~ M(t) - вход, а ~ y(t) – выход элемента.

Уравнение вала на основании второго закона механики (закона Ньютона) имеет вид:

,

где J – момент инерции вала. Заменяя 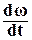на D, получаем уравнение вала в операторной форме

.

Последнее уравнение представляет частный случай уравнения (2) для m=0, n=1.

Как видим, выходной оператор Д(D)=JD, а входной K(D)=1.

Очевидно, что уравнение элемента зависит от того, какие сигналы принимаются в качестве выхода и входа. Так, если момент вращения

- входной сигнал, то, полагая, что

,

где 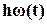- момент вязкого трения, h - коэффициент вязкого трения, то уравнение вала принимает другой вид

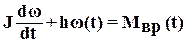
или

.

Отсюда

Д(D)=JD+h, K(D)=1.

Найдите сами уравнение вала для случая, когда входом является момент вращения, а выходом угол поворота .

Наряду с операторной записью ДУ (1) в виде (2) будем использовать еще более компактную форму:

или

y(t)=W(D)v(t), (3)

где W(D) называется операторной передаточной функцией (ОПФ) или оператором з вена. Формально W(D) можно рассматривать как отношение двух многочленов от D:

W(D)=K(D)/Д(D), (4)

которое условимся записывать, не производя никаких возможных сокращений. Запись (4) является символической и не дает решения ДУ (2), т.к. не определено, какой смысл имеет деление на операторный многочлен Д(D).

2) Уравнение звена в изображениях. Передаточная функция звена (ПФ)

Напомним, что преобразованием Лапласа функции x(t) (ее изображением) называется интеграл

,

где x(t) при t<0, 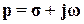- комплексная переменная.

В символическом виде функция x(p) записывается как

x(p)=L[x(t)],

где L – символ преобразования Лапласа. По заданному изображению x(p) может быть однозначно восстановлена функция x(t), называемая в этом случае оригиналом x(p). Эта операция в символическом виде записывается как

,

где оператор - символ обратного преобразования Лапласа.

Использование преобразования Лапласа для решения ДУ основывается, прежде всего, на теореме об изображении производной, согласно которой

L[Dx(t)]=px(p),

если х(0)=0. Из последнего выражения следует, что

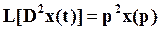
при и также, что

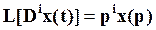, i>0, (*)

если 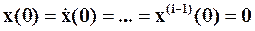. Часто эти начальные условия обозначают с аргументом - 0 и называют предначальными условиями. С учетом (*) и теоремы линейности преобразование Лапласа от произведения A(D)y(t), где A(D)= представляет собой операторный многочлен, определяется как

L[A(D)x(t)]=A(p)x(p), (**)

если .

Найдем преобразование Лапласа от уравнения (2):

L[Д(D)y(t)]=L[K(D)v(t)].

Используя (**), находим уравнение звена в изображениях

Д(p)y(p)=K(p)V(p), (5)

где y(p)=L[y(t)] – преобразование Лапласа от выхода, а v(p)=L[v(t)] – преобразование Лапласа от входа,

,

.

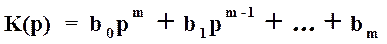Уравнение (5) имеет место, если выполняются следующие условия:

1)

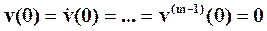
и

2) .

Заметим, что условие 1) всегда выполняется, т.к. v(t)=0, t<0, а условие 2) выполняется не всегда.

Если условия 1) и 2) выполняются, то звено предварительно невозбужденно (находится в покое до подачи входного воздействия).

Если условия 2) не выполняются, то звено называется предварительно возбужденным.

Уравнение (5) – алгебраическое уравнение, т.к. K(p) и Д(р) – алгебраические многочлены. Поэтому деление на Д(р) имеет обычный математический смысл, так что

.

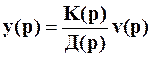Принимая во внимание уравнение (4), изображение выхода можно записать как

y(p)=W(p)v(p), (6)

где W(p) – передаточная функция (ПФ) звена, определяемая выражением

W(p)=K(p)/Д(p) (7)

или по определению выражением

W(p)=y(p)/v(p). (8)

Определение: ПФ звена – это отношение преобразований Лапласа выходного и входного сигнала предварительно невозбужденного звена.

Условие физической осуществимости звена имеет вид:

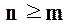
или

.

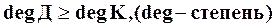Неполнота описания вход-выход с помощью ПФ заключается в следующем:

1) ПФ описывает свойства предварительно невозбужденного звена. Поэтому нельзя найти полное решение уравнения (1), а только при нулевых начальных условиях.

2) Исходное уравнение звена можно восстановить по ПФ, используя выражение

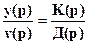
и применяя затем обратное преобразование Лапласа лишь, если многочлены К(р) и Д(р) не содержат одинаковых сомножителей. Только в этом случае знаменатель ПФ Д(р) называют характеристическим многочленом звена.

Если К(р), Д(р) содержат общие сомножители, то многочлен Д(р) не равен знаменателю вырожденной передаточной функции, т.е ПФ, получаемой после сокращения сомножителей.

The input- output relationship in a linear time invariant system is defined by the transfer function.

The features of the transfer functions are,

(1) It is applicable to Linear Time Invariant system.

(2) It is the ratio between the Laplace Transform of the o/p variable to the Laplace Transform of the i/p variable.

(3) It is assumed that initial conditions are zero.

(4) It is independent of i/p excitation.

(5) It is used to obtain systems o/p response.

An equation describing the physical system has integrals & differentials, the step involved in obtaining the

transfer function are;

(1) Write the differential equation of the system.

(2) Replace the terms 􀯗

􀯗􀯧 by ‘S’ & 􀗬 􀝀􀝐 by 1/S.

(3) Eliminate all the variables except the desired variables.

Пример. Пусть звено описывается уравнением 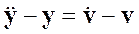и входной сигнал v(t)=t. Известны начальные условия у(0) и . Тогда решение уравнения определяется выражением

,

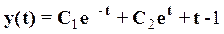где С₁ и С₂ находятся с помощью начальных условий.

Найдем ПФ звена. С этой целью преобразуем по Лапласу уравнение звена:

.

Характеристический многочлен звена равен

.

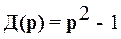При нулевых начальных условиях получаем уравнение в изображениях

.

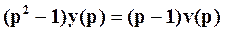Отсюда ПФ звена после сокращения числителя и знаменателя на общий сомножитель принимает вид вырожденной ПФ:

.

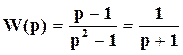Восстановленные по вырожденной ПФ уравнения

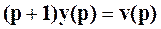
и

не совпадают с исходными уравнениями.

Решая последнее уравнение при v(t)=t, мы получим .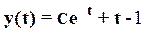

Решения исходного и восстановленного уравнений будут совпадать только при нулевых н.у. Знаменатель ПФ не равен характеристическому многочлену, т.е.

.

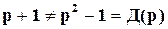Дата добавления: 2014-01-07